简单案例为主线的《信息安全数学基础》教学模式研究
刘淑娴,杨文忠
(新疆大学信息科学与工程学院,乌鲁木齐830046)
0 引言
随着人们对信息安全的重视,信息安全领域越来越受到关注,信息安全学科是一门新兴的学科,涉及通信学、计算机科学、信息学和数学等多个学科。应用于信息安全的数学理论和知识涉及数论、代数系统、椭圆曲线论等,为此,信息安全专业的学生需要学习《信息安全数学基础》课程。《信息安全数学基础》不仅作为信息安全专业的基础课程,更是信息安全专业的专业数学课程。奠定良好的数学理论基础,有利于提高学生对后续课程(如:现代密码学、网络安全基础、协议分析等)的学习兴趣。没有基础,就没有进阶,知识体系环环相扣,是统一的整体,没有夯实的基础,就像木桶中的短板一样,最终会成为影响专业系统性学习的瓶颈。本文通过分析信息安全专业学生在学习过程中存在的问题,探讨以简单案例为主线的教学模式,使学生更容易掌握相关知识点。
1 目前存在的问题
习近平总书记明确指出,网络安全和信息化是事关国家安全和国家发展、事关广大人民群众工作生活的重大战略问题,要从国际国内大势出发,总体布局,统筹各方,创新发展,努力把我国建设成为网络强国。党的十八届五中全会明确提出实施网络强国战略。
作为地处祖国西北边陲的新疆,网络安全建设不容忽视,2006年新疆大学信息科学与工程学院开设信息安全专业,成为新疆维吾尔自治区第一所开设信息安全专业的高校;2012年新疆大学信息安全专业被批准为第二轮新疆维吾尔自治区紧缺专业;2017年新疆大学信息安全专业获批为新疆维吾尔自治区战略新兴专业。
习近平总书记强调,高校思想政治工作关系高校培养什么样的人、如何培养人以及为谁培养人这个根本问题。要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程,实现全程育人、全方位育人,努力开创我国高等教育事业发展新局面。
新疆大学担负着培养思想政治过硬、基础理论功底扎实、专业技术熟练的信息安全人才的重要使命,不仅关系着新疆地方经济建设和发展,更关系着新疆的社会稳定和长治久安总目标的实现,关系着国家的网络安全事业。
目前新疆大学信息安全专业学生在学习《信息安全数学基础》课程中,主要存在以下3方面问题。
1.1 同一专业学生数学基础不同
2018年7月至8月,新疆大学面向全国27个省(自治区、直辖市)共录取普通本科新生5098人,其中,省内新生3500人(包括民语言新生),省外新生1598人。各省市的生源质量不均衡,对于新疆维吾尔自治区的学生来说,南疆和北疆的教学质量也不均衡,因此学生的数学基础不同,对《信息安全数学基础》课程的学习有较大的影响,为了更加深入掌握《信息安全数学基础》背后的算法,理论基本功的学习与训练是不可缺少的。
1.2 教学案例选择考虑不充分
《信息安全数学基础》课程教学内容主要包括两大部分:数论和群论。在数论学习中,了解掌握各种计算方法,并知晓与后续课程之间的关系,教学中如若强调各种定理证明,部分学生本身数学底子薄,对证明的理解存在困难,从而造成学生在学习中没有成就感,感受不到学习的乐趣。在数学和抽象代数中,群论研究名为群的代数结构。群在抽象代数中具有基本的重要地位:许多代数结构,包括环、域等,可以看作是在群的基础上添加新的运算和公理而形成的。在群论学习中,由于内容比较抽象,若选取的案例不合适,会造成学生不能充分理解基本概念,从而导致学生对数学学习望而生畏。
1.3 教学手段较落后
由于课时有限,在有限的课时里为了完成教学任务,课堂教学仍以传统教学手段为主,没有真正体现“授人以渔”的理念,不能充分发挥学生的主观能动性,仅满足于上课听课、下课完成作业、考试合格的基本要求,未能将数学学习与专业学习相结合,未达到以数学理论功底带动专业算法实践的目的。
2 应用实例
案例教学法起源于上世纪20年代,由美国哈佛商学院所倡导,当时是采取一种很独特的案例型式的教学,这些案例都是来自于商业管理的真实情境或事件,透过此种方式,有助于培养和发展学生主动参与课堂讨论,实施之后,颇具绩效。上世纪90年代末,国内教育界开始探究案例教学法。该方法能鼓励学生独立思考;引导学生变注重知识为注重能力;重视双向交流。
1.1 研究对象 选取2015年1月至2017年6月在我院诊断为SUI的女性患者120例为病例组,同期选取无症状健康女性70例为对照组。病例组年龄25~66(47±13)岁,对照组年龄21~70(39±18)岁,统计两组女性体质量指数(body mass index,BMI)、孕次、产次。所有入选女性均无急性妇科、泌尿系炎症,无盆腔巨大包块史,无盆底手术、盆底外伤,无慢性咳嗽便秘史,无严重内、外科疾病,近3个月内无激素替代治疗。
由于《信息安全数学基础》课程具有基础性、系统性、前沿性、专业性和工程性,若在教学中选择的案例过于复杂,不仅影响教学效果,也会降低学生的学习兴趣。本文所提出的简单案例是指内容单一,容易理解、使用或处理的教学范例。通过简单案例,让学生学会如何运用数学的基本原理来处理实际问题,懂得与后续课程之间的衔接。
选取简单案例的主要原则:
(1)简单。选择计算容易的问题,能够反映数学问题的实例进行讲解。
(2)主线特点明显。采取“以点带面”的方式,通过一例的学习,延续至后续各知识点中,其结果也能够继续复用。
(3)举一反三。数学学习的特点是概念多、计算量大,在教学中通过简单案例的分析,让学生迅速掌握知识点,在作业及后续学习中,循序渐进,学会解决更为复杂的数学问题。
在《信息安全数学基础》课程教学中,教师根据教学大纲,依次为学生讲授整数的可除性、同余、同余式、二次同余式与平方剩余、原根与指标、素性检验、群、群的结构、环与理想、多项式环、域和Galois理论、域的结构、椭圆曲线等内容。在这一系列问题的学习中,我们完全可以用简单案例作为主线,将各学习点通过这一主线串起来。例如:我们在这里采用两个整数a和m,令a=5,m=17,设计合理的案例,将欧几里得除法、最大公因数和最小公倍数、同余、剩余类、欧拉定理、同余式求解、平方剩余、原根、群、有限域及椭圆曲线等知识点贯穿在一起。
由于涉及知识点较多,本文仅选取欧几里得除法、最大公因数、原根和有限域等4个知识点进行介绍,涵盖了数论到群论的重要知识点。
2.1 学习欧几里得除法
欧几里得除法定义为:设a,m是两个整数,其中b>0。则对任意的整数c,存在唯一的整数q,r使得a=q·m+r,c≤r 若令 a=17,m=5,取整数 c=0,0≤ r<5。若 q=0,则17=0·5+17,但是17不在0≤r<5的取值范围;若q=1,则 17=1·5+12,若 q=2,则 17=2·5+7,但是 12、7 均不在0≤ r<5 的取值范围;若 q=3,则 17=3·5+2,2 在 0≤ r<5的取值范围;若 q=4,则 17=4·5+(-3),但是-3 不在 0≤r<5的取值范围。因此a=17,m=5,取整数c=0时,由欧几里得除法定义可知 17=3·5+2,即:q=3,r=2。 以上两例说明,不论a与m的大小关系如何,欧几里得除法均适用,并且通过上述分析,为学生引入q与r的表示式,即:不完全商,余数 r=a-q·m。 根据定理:设a,m,r是三个不全为零的整数,如果a=q·m+r,其中 q 是整数,则(a,m)=(m,r)。 以及最大公因数的定义,我们引出广义欧几里得除法(也叫辗转相除法)求解两个整数的最大公因数。 设a,m是任意两个整数,记r-2=a,r-1=m,反复运用欧几里得除法,有: 案例设计:令 a=17,m=5,则:r-2=17,r-1=5,反复运用欧几里得除法,有: 所以,(17,5)=1,并且对于(a,m)=1,称 a与 m 互素,本例中a=17与m=5互素。 要学习原根,首先要了解指数的概念:设m>1是整数,a是与m互素的正整数,则使得ae≡1(mod m)成立的最小正整数e叫做a对模m的指数,记作ordm(a)。如果a对模m的指数是φ(m),则a叫做模m的原根。 案例设计:令 a=5,m=17。 求解mod 17的原根有多种方法: (1)根据定义,直接计算判断a=5是否是模m=17的一个原根。 所以,Ord17(5)=φ(17)=16,即a=5是模m=17的一个原根。 (2)由欧拉定理,aφ(m)≡1(mod m),(a,m)=1,所以ordm(a)|φ(m)。 所以,对于原根判断,我们只需考察φ(m)的因数d,即:d|φ(m)。 上例新解:令 a=5,m=17。 对比第一种方法,第二种方法的效率要更高。 (3)m=17是奇素数,根据定理,m-1的所有不同素因数是 q1,…,qs,则 a是模 m原根的充要条件是 m-1=17-1=16=24,所 有 不 同 素 因 数 q=2,因 所以,a=5是模m=17的一个原根。 有限域是信息安全领域中一个非常重要的概念,扎实掌握这一知识点,对于椭圆曲线的学习非常重要,同时也体现在后续课程的学习中,如:现代密码学等。 为了让学生较轻松地掌握有限域地概念,我们不妨利用之前学生已经较好掌握的知识进行扩充,首先以GF(p)为例进行有限域学习的引入。 根据原根知识点的学习,a=5是模m=17的一个原根,所以a=5是有限域GF(17)的一个生成元,并且GF*(17)的所有元素,都可以表示为 ai(mod m),i=0,1,…,φ(m)-1。 在多年《信息安全数学基础》课程教学中,为了提高教学质量我们一直寻求突破点,运用多种教学手段,不断提高学生的学习兴趣。经过多年教学与实践,本文倡导的以简单案例为主线的教学模式已取得初步成果,以本文案例为例,在教学中能有效地促进学生对知识点地理解,并且能体会知识的系统性和连续性,收到了较好的教学效果。2.2 学习最大公因数
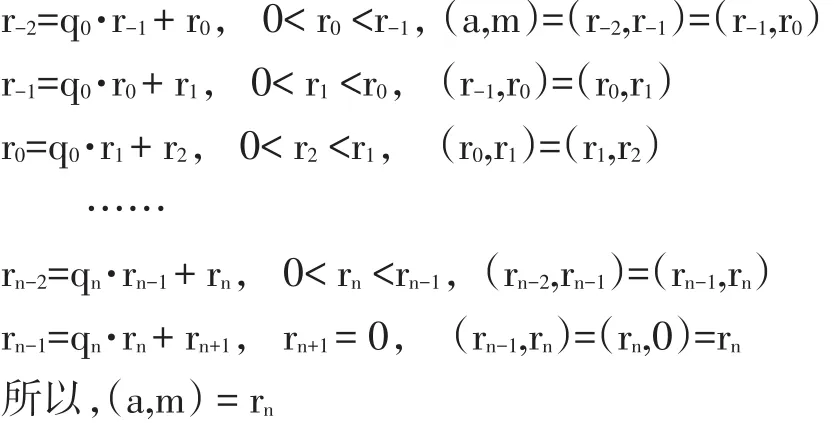
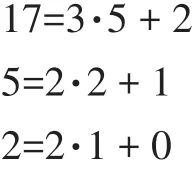
2.3 学习原根
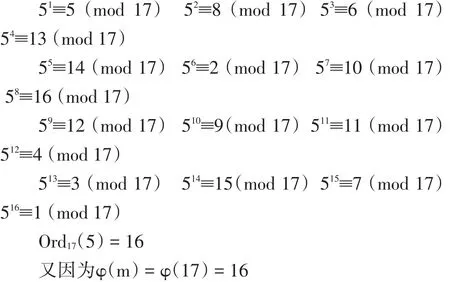

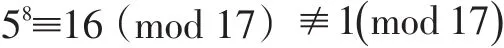
2.4 学习有限域
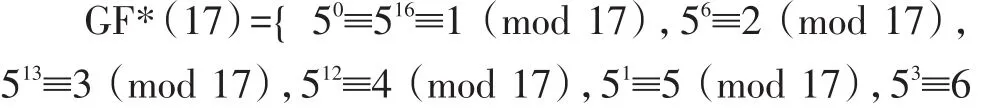
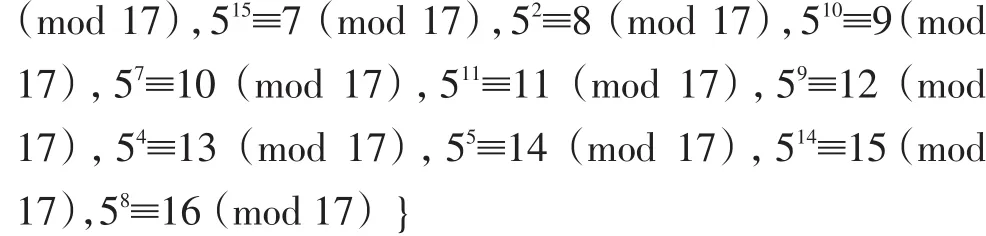
3 结语

