一类广义Wiener非线性系统的参数辨识算法

景绍学 范梦松 李冬梅

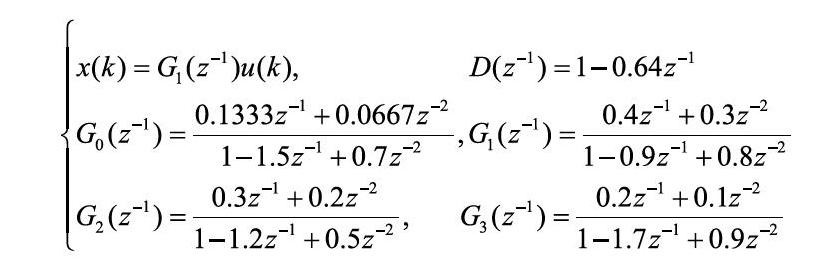
摘 要：传统的Wiener系统在工业系统建模方面获得了大量应用，但是当系统含有动态非线性环节时，就会因为模型不匹配导致建模效果不佳。为了更好的对这类系统进行建模，必须将传统Wiener系统中的静态非线性模块扩展为动态非线性形式。在采用全新结构的基础上，基于关键项分离技术参数化系统以减小算法计算量，并避免出现参数乘积项；对数据进行滤波以获得参数的无偏估计；运用最小二乘算法以获得健壮的参数估计值。数值仿真表明了算法的有效性。

关键词：参数辨识；广义Wiener系统；关键项分离；最小二乘算法

中图分类号：TP391.9 文献标识码：A

Abstract：The traditional Wiener system has been widely applied in the modeling of industrial system.However，when the system contains dynamic nonlinear elements，the model obtained is not optimal because of the non-matching model.In order to model this kind of system better，the static nonlinear block in the traditional Wiener system must be extended to dynamic nonlinear form.Firstly，the original system with new structure is parameterized based on key-term separation technology to reduce the computation，and to avoid the product terms of the parameters；secondly，the input and output data are filtered to estimate the known parameters without bias；At last，the least squares algorithm is used to obtain robust parameter estimates.Numerical simulation shows the effectiveness of the algorithm.

Keywords：parameter identification；generalized Wiener systems；key-term separation；least squares algorithm

1 引言（Introduction）

模塊化非线性系统因其结构简单、适用性强，在非线性系统的建模过程中获得了广泛应用[1-3]。从构成上看，典型的模块化非线性系统有Wiener系统、Hammerstein系统和Hammerstein-Wiener系统等。其中传统的Wiener系统是由一个线性动态模块串联一个非线性静态模块构成的，大量的实际的非线性系统可以用Wiener系统进行描述，如化学系统、生物系统和混沌系统[4-6]，等等。由于Wiener系统含有的输出非线性环节，导致其辨识难度很大，辨识算法相对较少[7，8]。Wiener系统的辨识算法有如下特点：

（1）由于辨识难度大，智能优化算法在Wiener系统的辨识算法中占据了重要地位。如，吴德会基于一种新型的神经网络结构辨识Wiener模型参数[9]。张艳、李少远等人利用粒子群优化算法对Wiener非线性系统的辨识问题进行了研究[10]。Tan、Al-Duwaish等人基于遗传算法讨论了Wiener系统的辨识问题[11-13]。

（2）最小二乘算法和极大似然算法也被经常用于Wiener系统的参数辨识中。如，最小二乘迭代辨识算法、递推最小二乘算法和极大似然辨识算法[14-16]。

目前，在模块化非线性系统的辨识问题中，考虑的非线性模块多为静态的，即非线性模块的输出只与其当前时刻输入有关。然而，事实并非总是如此，为了更好的逼近实际系统、获得更加满意的辨识效果，本文将动态因素引入模块化非线性系统的非线性部分，构成了广义模块化非线性系统。本文研究一类典型的广义模块化非线性系统——广义Wiener系统的参数辨识问题。广义Wiener系统（Generalized Wiener systems，GW）由一个线性动态子模块后面串联一个动态非线性模块组成，其辨识难点包括：（1）两个环节中间的变量不可测，现有辨识方法无法直接应用；（2）直接参数化后导致出现参数乘积项，无法得到单个环节的参数；（3）系统的辨识参数化后系统维数很高，辨识算法的计算量很大。

针对一类有色噪声扰动的GW系统，本文首先以一种新的结构形式描述这类系统，随后利用关键项分离技术参数化系统，然后对输入输出数据进行滤波，将有色噪声白化为白噪声，再使用递推最小二乘算法获得无偏估计。最后用数值仿真验证了算法的有效性。

2 问题描述（Problem description）

考虑如图1所示的一类广义Wiener系统。它由前向线性传递函数、前向非线性传递函数、输出负反馈传递函数和噪声传递函数组成。图中，、分别系统的输入和输出，为一个均值为零方差为的高斯白噪声，、和为不可测中间变量。可以看出，系统的非线性传递函数是动态的。

值得注意的是，式（3）中的信息向量中除了已知外，其他变量都是未知的，可以用它们的估计值代替。为了提高参数估计值的精度，采用滑动窗口指数平均技术对中间变量（关键项）进行了处理。

由于本算法是基于关键项分离技术和最小二乘算法的，所以该算法被命名为关键项分离的最小二乘算法（KTS-RLS）。算法的步骤如下：

Step 1：初始化；

Step 2：收集输入输出数据；

Step 3：基于关键项分离技术参数化系统；

Step 4：对输入输出数据进行滤波；

Step 5：用RLS算法对参数向量辨识；

Step 6：用RLS算法估计噪声传递函数参数；

Step 7：令，如果，转Step 2；否则，辨识结束。

4 数值仿真（Numerical simulation）

考虑如下的广义Wiener系统：

仿真时，输入序列采用幅值范围在的均匀分布随机数，噪声序列采用均值为零方差为的高斯白噪声序列，系统的输入、输出数据分别如图2和图3所示。利用本文提出的KTS-RLS算法，得到的辨识结果如表1所示。不同噪声方差下参数估计误差的变化情况见图4。从图和表中可以看出，随着辨识的进行，参数估计误差逐渐减小，各参数估计值向真值方向收敛。并且参数估计误差随噪声水平的增加呈增大的趋势。

5 结论（Conclusion）

为了辨识含有动态非线性模块的广义Wiener非线性系统，本文以一种新的结构形式描述这种系统，然后利用关键项分离技术参数化系统，并用滤波技术将原系统的有色噪声白化成白噪声，最后运用最小二乘算法进行了参数估计。数值仿真表明，在不需要进行参数分离的基础上，算法可以以较小的计算量获得比较精确的辨识结果。

参考文献 （References）

[1] Wang D Q，Liu H B，Ding F.Highly Efficient Identification Methods for Dual-Rate Hammerstein Systems[J].IEEE Transactions on Control Systems Technology，2015，23（5）：1952-1960.

[2] 景绍学，李正明.Wiener系统的变聚点样条逼近递推贝叶斯算法[J].控制理论与应用，2017，34（1）：13-21.

[3] Yu F，Mao Z，Jia M.Recursive Identification for Hammerstein–Wiener Systems with Deadzone Input Nonlinearity[J].Journal of Process Control，2013，23（8）：1108-1115.

[4] Chen H F.Recursive Identification for Wiener Model with Discontinuous Piece-Wise Linear Function[J].IEEE Transactions on Automatic Control，2006，51（3）：390-400.

[5] Wigren T，Schoukens J.Three Free Data Sets for Development and Benchmarking in Nonlinear System Identification[A].Proc.2013 Eur.Control Conf.（ECC2013），2013：17-19.

[6] Dudul S V，Ghatol A A.Identification of A Typical CD Player Arm Using a Two-Layer Perceptron Neural Network Model[J].Proceedings of the International Joint Conference on Neural Networks，IEEE，2003，2：1157-1162.

[7] Bai E W，Reyland J.Towards Identification of Wiener Systems with the Least Amount of a Priori Information on the Nonlinearity[J].Automatica，2008，44（4）：910-919.

[8] Fan D，Lo K.Identification for Disturbed MIMO Wiener Systems[J].Nonlinear Dynamics，2009，55（1-2）：31-42.

[9] 吴德会.非线性动态系统的Wiener神经网络辨识法[J].控制理论与应用，2009，26（11）：1192-1196.

[10] 张艳，李少远，王笑波，等.基于粒子群优化的Wiener模型辨识与实例研究[J].控制理论与应用，2006，23（6）：991-995.

[11] Tang Y，Qiao L，Guan X.Identification of Wiener model using step signals and particle swarm optimization[J].Expert Systems with Applications，2010，37（4）：3398-3404.

[12] Tan W W，Lu F，Loh A P，et al.Modeling and Control of a Pilot Ph Plant Using Genetic Algorithm[J].Engineering Applications of Artificial Intelligence，2005，18（4）：485-494.

[13] Dotoli M，Maione G，Naso D，et al.Genetic identification of dynamical systems with static nonlinearities[C].Proceedings of the 2001 IEEE Mountain Workshop on Soft Computing in Industrial Applications.Blacksburg：IEEE，2001：65-70.

[14] Wang D，Ding F.Least Squares Based and Gradient Based Iterative Identification for Wiener Nonlinear Systems[J].Signal Processing，2011，91（5）：1182-1189.

[15] Hu Y，Liu B，Zhou Q，et al.Recursive Extended Least Squares Parameter Estimation for Wiener Nonlinear Systems with Moving Average Noises[J].Circuits，Systems，and Signal Processing，2014，33（2）：655-664.

[16] Hagenblad A，Ljung L，Wills A.Maximum Likelihood Identification of Wiener Models[J].Automatica，2008，44（11）：2697-2705.

作者簡介：

景绍学（1976-），男，博士，讲师.研究领域：系统辨识，参数估计.

范梦松（1997-），女，本科生.研究领域：系统辨识.

李冬梅（1997-），女，本科生.研究领域：系统辨识.