一种基于蚁群算法的带时间窗物流运输车辆路径优化方法

汪 越，王向前，刘 敏

安徽理工大学经济与管理学院，淮南,232000

1 相关研究与问题提出

随着对物流运输问题研究的不断深入以及对运送货物时间的要求越来越高，发现配送中心在安排货物运输时，加入时间窗限制运送时间能节约运输成本，提高车辆的利用效率，因此国内外对带有时间窗的车辆路径问题(Vehicle Routing Problem With Time Windows，VRPTW)采取了多种方法进行研究。

Juliandri等针对车辆路径选择问题，将车辆调度问题建模为线性混合整数规划问题，开发了一个结合启发式和精确的方法来解决模型，最终得出了一组车辆的调度最佳路线集[1]。Masutti等认为穷举法解决车辆路径选择时具有局限性，因此基于群体智能的运用，阐述了蜜蜂启发法求解车辆路径问题，最终得出了最优路线[2]。Akhand等将车辆路径选择问题转化为旅行商问题，并利用扫描聚类算法处理，算法得出的最优路线集优于原结果中的路线集[3]。

国内对于车辆路径优化的研究中，覃运梅等针对时间和地点对接要求而导致投递效率不够高的问题，利用遗传算法处理该问题，最终使得配送车辆数目最少和配送成本最小[4]。裴小兵等针对多目标车辆路径优化问题，利用改进遗传算法、SPSS聚类分析等方法，最终提高了车辆路径的优化率和准确率[5]。侯玉梅等为改善整车物流配送问题，设计了自适应遗传算法并运用成品汽车配送案例进行验证，最终在满足要求的基础上提高了经济效益[6]；麻存瑞等人设计了自然素编码来综合考虑快递件数量、汽车载重等要求，构建了符合快递配送路径优化的数学模型，最终得出当前快递车辆能够满足运输需求而不需更换运输车辆[7]。何小峰等提出量子蚁群算法，经实例检验该算法性能更优，有效避免了车辆路径优化问题陷入局部最优及收敛速度较慢的问题[8]。

上述文献对车辆路径优化问题进行了详细研究，但是只选取了一个指标来阐明路径优化的过程，容易造成配送路径减少时，空载率及配送成本增大，因此本文利用配送路径长度和配送车辆空载率两个指标，对带时间窗物流运输车辆路径优化问题进行研究。

2 配送模型的建立

2.1 配送模型参数定义

已知客户的需求量及地理位置的情况下，配送中心利用m辆配送车为n个客户提供配送服务，设N=2,…,n为客户集合，配送中心赋为1，则在配送网络图中顶点集合为D=1∪N，配送车集合为K=1,2,3…,m。设车辆从配送点出发的时刻为T0，配送车辆到达客户i的时刻为T，客户i允许接受服务的最早和最晚时间分别为ETi和LTi,设客户的需求量为Q，S表示车辆k所服务的客户集，S表示客户集中含有的客户个数，如果配送车辆提前到达客户i处则须等待的时间为W，客户i接受服务需要的时间为s，当配送车辆完成对i的服务后紧接着去往下一个客户点j，路径长度为d。

2.2 车辆配送路径模型

决策变量：

数学模型：

(1)

(2)

(3)

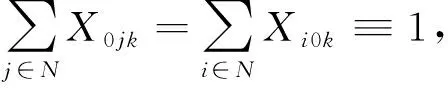
(4)

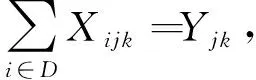
(5)

(6)

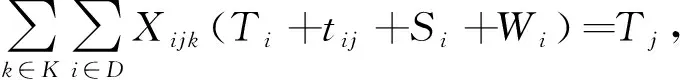
(7)

ETi≤Ti+Wi≤LTi,∀i∈N

(8)

X=Xik∈D

(9)

(1)表示配送车辆配送模型的目标函数，即配送车辆追求配送路径最小化的函数模型；

(2)表示车辆不能超载；

(3)表示每个客户只能由一辆车配送货物且只能接受服务一次；

(4)(6)表示从配送中心出发的车辆在完成配送任务后须回到配送中心，且配送时的路线不能形成回路；

(5)表示配送车在完成对客户i的配送服务后需要紧接着去下一个客户点j；

(7)表示配送车到达客户的时刻；

(8)表示客户的时间窗要求，配送车到达时间不能超出时间范围ETi，LTi；

(9)表示车辆k的线路必须是联通的。

3 配送车辆的蚁群算法模型表示

当配送车辆到达指定客户点，并完成相关任务后，只能移动到下一个未经过的客户点或者回到配送中心，不能再次向已经到达过的客户点移动。在满足上述配送车辆数学模型约束的条件下，当配送车辆到达一个客户点并完成配送任务后，接下来便会按照一定的规则选择下一个客户点，具体规则如下[9]：

(10)

S表示配送车辆下一个选择到达的客户点，U∈allowed表示配送车辆尚未到达的客户点集合，会优先在客户点V=(2,3,…,n)中选择向配送路径短的地点移动[10]。配送车辆每一次从配送中心至客户点的循环中，都会在尚未到达的客户点集合中选取下一个客户点，每次的路径都在不再减少，直至到最短路径，选择下一个客户点的概率公式如下：

(11)

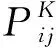
当一次循环结束后进入t+1时刻，此时各个路径由于路径长短不同，使得路径上的信息素残留不同，所以应对路径上的信息素做出调整和更新，本文对信息素进行全局更新，公式如下：

τijt+1=ρ·τijt+Δτijt,t+1

(12)

ρ为常数系数，表示信息素的持久率，其取值范围为[0,1]，所以ρτijt表示在时刻t时刻地点i到地点j的信息素残留量。m表示配送车辆表示在时刻t和时刻t+1中车辆k在客户点i到j路径上时所增加的信息素量。Q表示当车辆完成一次循环，即完成一次路径探索后所释放的信息素总和。lk表示车辆k在完成一次路径探索时的路径总长度。

求解步骤：

Step1设置最大迭代次数为N，令n=1，将各个参数进行初始化，将车辆放在配送路径中，计算出配送中心到各个客户点之间的距离以及各个客户点之间的距离。

Step2令配送车辆从初始位置即配送中心1出发，故i=1，接下来车辆将会随机到达下一个节点j，但必须满足约束条件(8)。当满足约束条件(8)后，对j进行卸载货物，当完成对j的任务时继续搜索下一个客户点，直到搜索完j的所有的相邻客户点。当没有客户点满足约束条件时，配送车辆将会从当前的客户点返回配送中心1，将此条路径作为解放入可行解集中。

Step3根据状态转移公式(11)，从步骤二中的可行解集寻找出路径最短的下一个最优节点j，根据节点j的需求量调整配送车辆的车载量。

近年来，河道整治工作一方面受到大众的普遍关注，另一方面又受到诸多因素的影响。当前基于生态环境保护的河道整治工作处于一个十分尴尬的位置，很难推进。这种尴尬的境遇是自然的发展与人类的需求不能很好融合以及一些宏观政策的影响。因此，河道整治工作需要做一些改变。传统的边岸固化方式未考虑到河流本身的特质，强硬的对自然环境加以干预和破坏。所以，现阶段的河道整治工作要重新规划，要考虑人的需要与河床演变的自然规律，考虑人与自然的关系，考虑河道演变的适度性，如此才能做出合理的河道整治方案[2]。

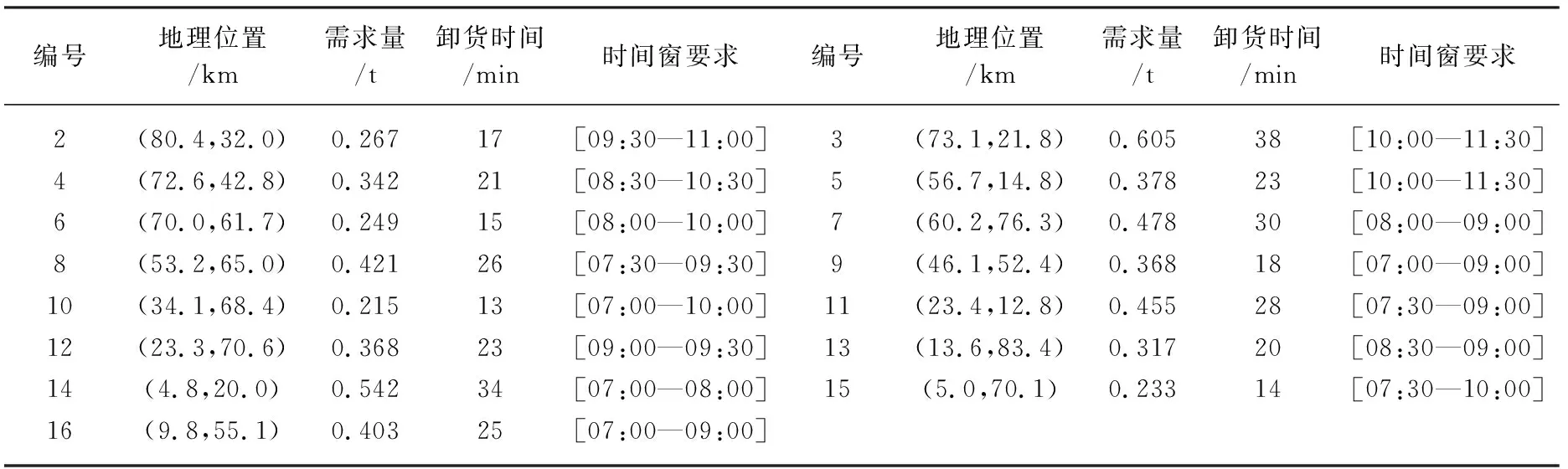
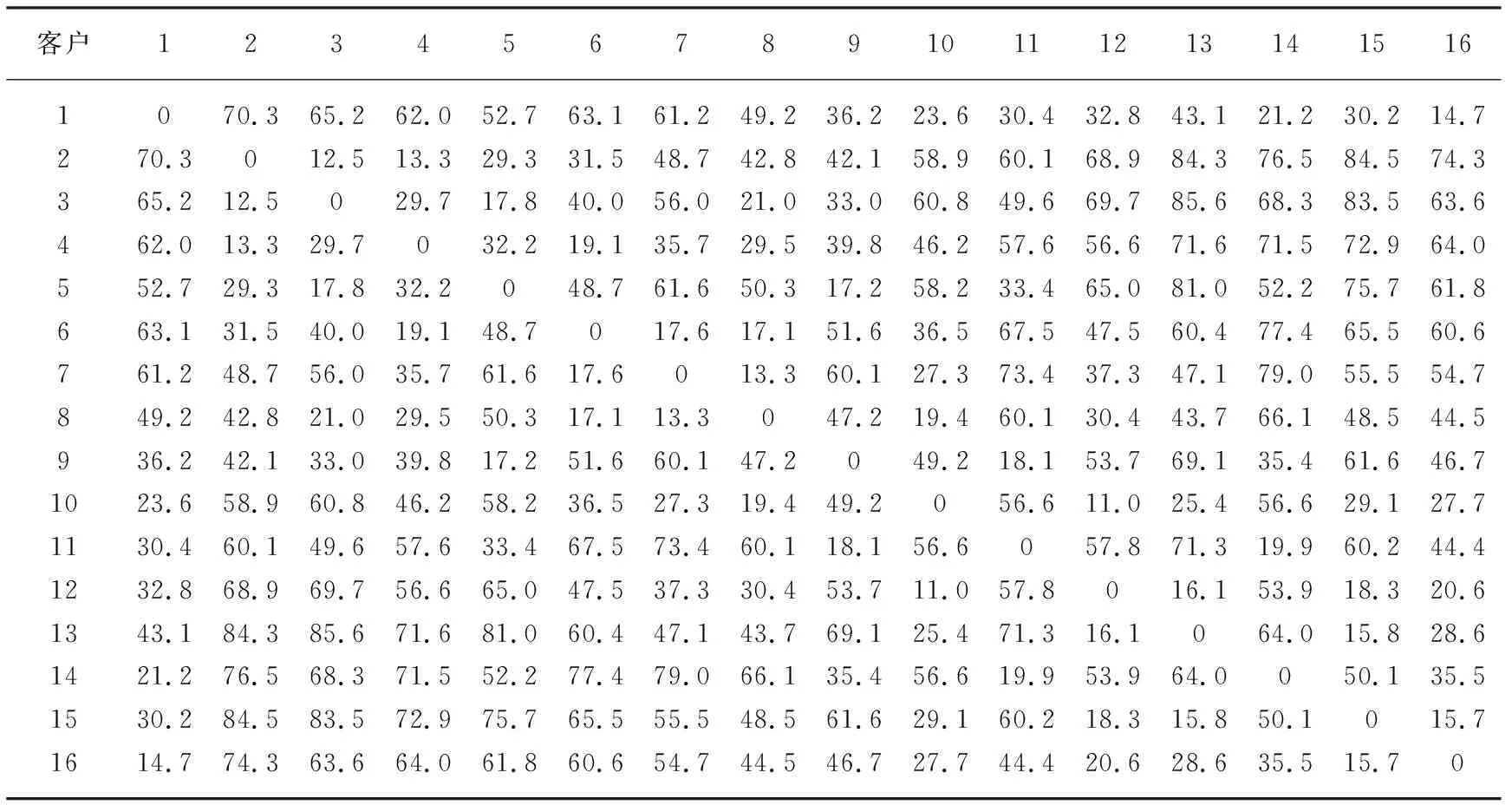
Step4当n

4 实例分析

现利用实例来检验上述模型的可行性，具体描述如下：淮南市有一主要从事电子产品的物流配送中心，共有4辆配送车辆，配送过程中平均速度为50 km/h，每辆车的最大载重量均为2.5 t，百公里油耗为11 L。配送中心编号为1，其地理位置为(10.6 km，40.4 km)，现在需要向15个客户点运送相关货物，配送中心每天自早上7点开始向各客户点配送货物，设单位卸货时间相同，客户点编号依次为2～16。15个客户的地理位置坐标、客户的货物需求量以及时间要求见表1。

表1 客户资料表

为方便算出各条路径的总路程,将表1的配送中心和客户点的距离制成距离矩阵如表2所示(假设各客户点距离均为直线距离且道路情况良好，在行驶过程中不存在耽误时间的意外情况发生)。

表2 配送中心及客户点距离矩阵表

该配送中心在未采用蚁群算法处理数据时，由于配送中心有4辆配送车，所以经常出现无论货物的多少都会使用4辆配送车配送货物的情况，这不仅使得配送成本加大，还会出现当新的货物到达配送中心时可能无法立即分配及无配送车辆可使用的情况，原配送路线、车辆到达时刻、运输量、空载率、总路程如表3所示。

表3 原车辆调度表

由表3可知，该物流配送中心原来在处理配送任务时，分配4辆配送车辆并形成了4条运输路线：第一条路线为：1→16→15→13→12→1，货运量为1.321 t，运输路程为95.1 km；第二条路线为：1→10→7→8→1，货运量为1.114 t，运输距离为113.4 km；第三条路线为：1→6→4→2→3→5→1，货运量为1.841 t，运输距离为178.5 km；第四路线为1→14→11→9→1，货运量为1.640 t，运输距离为95.4 km。4条路线的总运输量为6.01 t，并且四条路线的空载率均较高，其中第一条路线、第二条路线空载率高达47.16%、55.44%，4条路线的总路程为482.4 km，按照现行0号柴油油价6.55元/L，日行驶成本为348元。

表4 现车辆调度情况

由表4可知，该物流配送中心在处理带有时间窗的车辆路径选择时，分配3辆配送车辆来运输货物会使得车辆的运输距离最短，第一条路线为：1→16→15→13→12→10→1，货运量为1.536 t，运输总路程为96.9 km；第二条路线为：1→8→7→6→4→2→3→1，货运量为 2.362 t，运输距离为190.2 km；第三条路线为：1→14→11→9→5→1，货运量为2.112 t，运输距离为129.1 km。三条路线的总运输量为6.01 t，3条路线的总路程为416.2 km，该路线日行驶成本为300元，该距离比表3的总路程少，该结果符合数学模型中的约束条件。

将表3和表4的最终结果做比较(见表5)，可以得出当蚁群算法处理带有时间窗的车辆路径问题时，不仅会降低车辆路径的距离，还会大幅降低车辆的空载率，提高了车辆的利用率，降低了运输成本。

表5 对比表

5 结 论

物流的配送过程是向着低成本、高效率的方向发展的，在配送车辆载重量已知的情况下可以通过一系列算法来优化车辆路径选择问题以达到减少配送距离及配送车辆数的目的[13]。本文利用蚁群算法处理配送中心的现行车辆调度情况，为了解决优化指标过少的问题，在得出配送路径长度减少的情况下，增加了车辆空载率指标，对蚁群算法优化车辆路径问题做了进一步阐述，得出该配送中心现行车辆调度需要改进。

虽然对车辆的路径优化问题研究较早，但仍有许多方面需要改进，例如，如何平衡车辆路径距离、配送成本、空载率等各项指标的重要性问题，车辆行驶过程中的成本变动问题，路况所导致的配送时间变动问题等，因此在配送过程中需要综合考虑各种因素以及各因素间的影响关系，使得物流配送效率得到进一步提高。