河堤决口预测及溃堤洪水的矿井风险评价模型*
胡苏安 何盈利 姜宝元 余子文 高 岳
(中国矿业大学资源与地球科学学院)
我国东部地区许多煤矿毗邻水库、河道等地表水系,开采使得诸如地表塌陷、地裂缝等一系列地质灾害逐渐产生,并成为地表水下渗的良好通道,尤其是处于河道附近的矿区,在暴雨等极端天气下,极易发生淹井、涌水、突泥等事故。近年来,针对河道溃堤及溃堤水流的研究主要采用数值模拟方法,刘丽玲等[1]进行了河道与渐溃堤坝耦联的水力数值模拟;郑国栋等[2]对Abbott六点中心格式的应用进行了研究,确定了其适用性;陆灵威等[3]通过在大型室内水槽中进行物理模型试验,模拟分析了溃堤后洪水在溃口外洪泛区内的演进和落水波在河道内的传播过程;国际上,美国气象局的溃坝洪水预测模型(DAMBREAK)和简化溃坝洪水预测模型(SMPDBK),美国土保局的简化溃坝演进模型(TR66),以及荷兰DELFT大学的洪水系统(DELFTFLS)等相继问世,并在工程实践中得到了广泛应用[4],为河堤决口预测及溃堤洪水演进分析提供了理论依据。在洪水风险评估方面,陈华丽等[5]综合考虑了影响洪水灾害危险性和社会经济易损性的因素,对湖北省的洪水灾害风险进行了评价;Masatoshi[6]对日本109个河流水系的洪水风险性进行了评价,并进行了不同水系的洪水风险分区研究。本研究在上述成果的基础上,以河堤决口处的流量、水位等水力参数建立河堤决口预测模型,再引入矿井井口到河堤各区段路线的阻碍因子总值得到溃堤洪水淹没分区模型,从而对堤坝决口的洪水淹井风险进行安全评价。
1 河堤决口预测模型
1.1 一维单一河道水力模型
1.1.1 一维河道水力模型的基本原理
描述一维水流运动的方程组为Saint-Venant方程组[7],该方程组建立在质量和动量守恒的基础上,以水位和流量为研究对象,表达式为
(1)
式中,Q为流量;h为断面水位;A为过水断面面积;g为重力加速度;q为河流单位旁侧入流量;x为空间坐标;t为时间坐标,C为谢才系数;α为垂向速度分布系数;R为水力半径,m。
1.1.2 方程组离散
选用Abbott六点中心格式[2]进行方程组求解,河道断面按照水位(h)—流量(Q)—水位(h)的顺序交替布置(其中,Q和h不在同一个断面上(图1),Q总是布置于相邻的h之间,距离可以不相同),而后在每个时间段内,利用隐格式的差分法交替计算Q和h[2]。
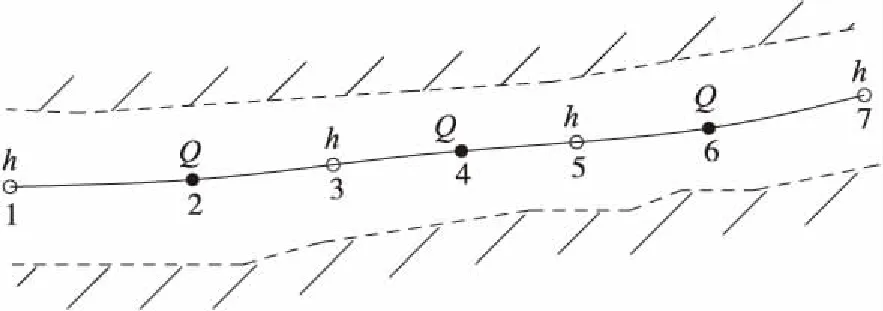
图1 河道断点布置示意
在连续方程中,Q仅对x求偏导,所以方程容易写成以h为中心的形式(图2),动量方程仅以Q为中心(图3)。

图2 连续方程Abbott六点中心格式[2]
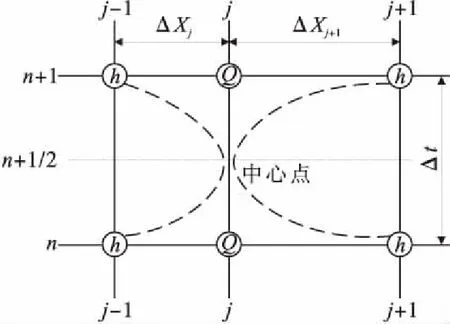
图3 动量方程Abbott六点中心格式[2]
在n+1/2时刻,连续方程的离散形式可以表示为
(2)
动量方程的离散形式可以表示为
(3)
式(2)、式(3)中的α、β、γ及δ为方程的计算系数。
1.1.3 离散方程求解
假设1条河流有n个节点,若河道首、末水位点都是h点,n为奇数,于是n个线性方程有n+2个未知数,多出的2个未知数来源于首、末水位点,Zj-1、Zj+1分别变成河流上下游的水位节点,即:h1=Hus,此时系数α1=-1,β1=1,γ1=0,δ1=0[2]。同理,末断面上hn=Hds,此时系数αn=0,βn=1,γn=-1,δn=0。只要知道上下游水位Hus和Hds,如此n个方程左边有n个未知数,可以使用标准消元法进行求解。此时,任意节点的变量Z(水位或流量)可以表示为上下游水位节点的函数:
(4)
式中,c、a、b分别为计算系数。
1.2 河堤决口过程模拟
DAMBRK模型[8]将河堤决口概化成梯形,本研究建模时对决口演变过程进行了一定程度简化处理,不对泥沙输运进行计算,并且假定决口尺寸按指数形式扩大。决口处的流量采用Freed堰流公式进行计算。对比于其他模型,该模型较简单,求解所需参数较少,易于进行工程应用。
1.2.1 河堤决口模拟
本研究针对所研究的土堤将决口模拟为梯形(图4)[9-13],并按照河堤逐渐溃决进行计算。假设整个溃决过程的总历时为T,河堤从顶部某一点开始溃决,在溃决过程中,溃口形状按照线性比率扩大,到达T时刻时,决口宽度达到最大,决口底部高程为最终高程hbm。
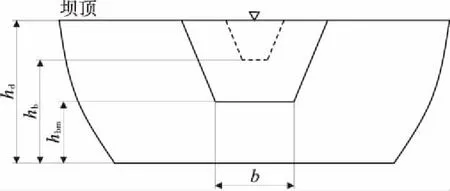
图4 河堤决口示意
溃决模拟过程中,决口的底部高程和底部宽度为时间的函数,随着时间的变化而变化。决口底部高程计算公式为
(5)
式中,hb为瞬时决口的底部高程,m;hd为堤防总高,m;hbm为决口稳定时的底部高程,m;tb为开始发生溃决至计算时刻经历的时间;T为溃决到达稳定的总历时;ρ0为决口处的非线性程度因子,本研究认为河堤决口尺寸按线性变化,故ρ0=1。
决口底部宽度的计算公式为
(6)
式中,bi为瞬时决口的底部宽度,m;b为决口稳定时的底部宽度,m。
1.2.2 河堤决口处流量计算
针对线性梯形决口流量,本研究采用宽顶堰流公式[9-11]进行计算
Qb=cvks[3.1bi(h-hb)1.5]+2.45z(h-hb)2.5,
(7)
式中,cv为流量校正系数;ks为考虑尾水影响出流的淹没校正系数,由于决口下游为干底,故不考虑决口下游尾水影响,取ks=1.0;h为决口上游水位,m;z为决口边坡系数。
2 溃堤洪水淹没分区模型
2.1 层次结构模型构建
首先将整个系统问题进行有条理有层次的分析,从而构建一个具有层次结构的模型,并在层次模型下,将复杂的问题分为系统元素的组成部分。综合分析该类系统元素,按照其性和关系构成若干个层次,上层元素作为支配下层元素的准则,系统元素可以分为3个层次(最高层、中间层、最底层)。对决口洪水行进过程进行4个方面的影响因素指标综合分析以及对各种主要评价因素进行划分,可以构建决口洪水行进过程的影响指标体系,其中最高层为溃堤洪水行进过程影响因素,中间层有地形条件、地表状况、地表状况、地质特征和监督管理4个方面的因素,最底层中地形条件包含有坡向、高度和连通性,地表状况包含有道路覆盖、房屋覆盖、植被覆盖和裸地覆盖,地质特征包含有砂土、黏土和基岩,监督管理包含有管理制度、日常维护运行、紧急备案维护和其他人为因素。决口洪水行进过程影响指标体系构建完毕后,选取一种科学可靠的分析方法来评价决口洪水行进过程影响指标等级是获得切合实际的评价结果的关键所在。本研究选用层次分析法[14]进行评估。
2.2 建立判断矩阵
两两比较判断矩阵构建的目的是衡量各个准则指标之间的相对重要性,衡量方法一般采用Satty提出的1~9 值法(表1),从而得到两两比较重要性标度构成的判断矩阵[15-17]。

表1 判断矩阵标度定义
2.3 判断矩阵一致性检验
层次分析法中需要对判断矩阵的一致性进行检验,本研究引入了检查判断思维的一致性指标CI(Consistency Index):
CI=(λmax-n)/(n-1) ,
(8)
式中,λmax为判断矩阵的最大特征值;n为判断矩阵的阶数。
在上述分析的基础上,查找一次性指标RI(表2)[18],而后计算一致性比率CR(Consistency Ratio):
CR=CI/RI .
(9)
通过层次分析法并进行一致性检验后,当CR<0.10时,认为判断矩阵的一致性检验是可以接受的,否则,应对判断矩阵作适当修正。
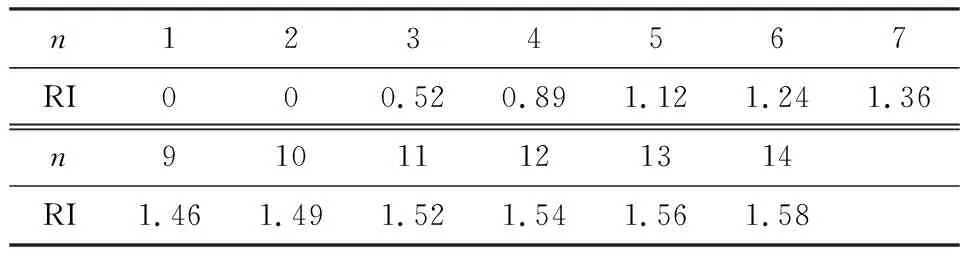
表2 平均随机一致性指标[18]
2.4 最终权重计算结果
经过层次分析法计算,得到了如表3所示的各中间层和最底层的权重。
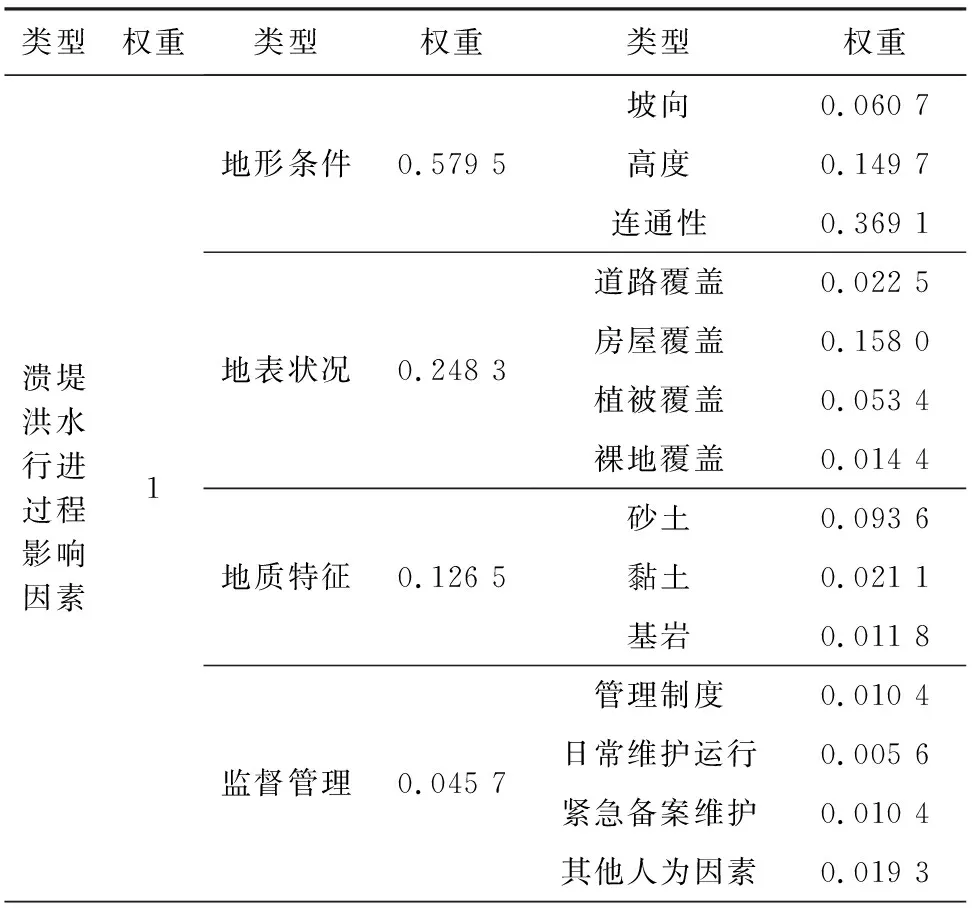
表3 溃堤洪水行进过程影响因素评价体系
3 实例分析
3.1 计算实例
本研究以山东新泰煤矿溃水事故为例进行分析,2007年8月15日夜间开始,山东新汶突降暴雨,山洪暴发,导致柴汶河东都河堤被冲垮,致使河堤发生决口。河堤长度500 m,河堤顶部高程为170 m,计算时间为2007年8月15日0:00:00至2007年8月22日0:00:00,从2007年8月15日20:00:00 开始河堤发生决口。溃决历时35 h,决口边坡系数为1.0,决口变化过程呈线性,流量校正系数取1.0。河道上游水位为169 m,河道底部糙率为0.03,底坡坡降为0.000 5,河道总长116 km,发生溃决时河道上游恒定流量为1 800 m3/s,下游恒定流量为900 m3/s,溃决时从侧向溃。
3.2 计算结果分析
根据一维河道水力模型和DAMBRK模型进行耦合计算,得到了如图5~图7所示的决口流量与决口水位、决口宽度及决口水流流速的过程曲线。
由图5可知:2007年8月15日夜间开始溃决,随着时间的增长流量急剧增大,大约35 h后达到峰值流量900 m3/s,随后流量逐渐减小,大约85 h后流量起伏不大,并与河道中上下游流量相平衡;在此过程中水位变化初期与流量变化趋势相似,在8月15日夜间溃决开始后流量随着时间急剧增大达到最大水位169 m,之后水位随时间降低,且降低速率较快,大约 72 h 后水位达到稳定。
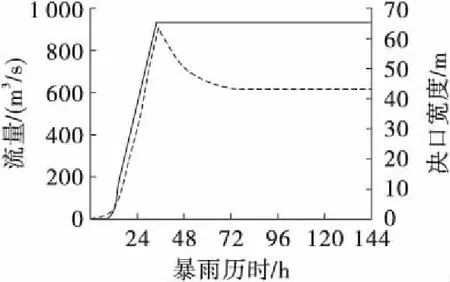
图6 溃决流量-决口宽度过程曲线
河堤溃决期间,本研究假设决口变化呈梯形线性增大。由图6可见:在溃决初期,河堤决口随时间急剧增大,此后决口宽度扩大速度有所减慢,最终达到最大值65 m,之后决口宽度基本固定,变化很小。
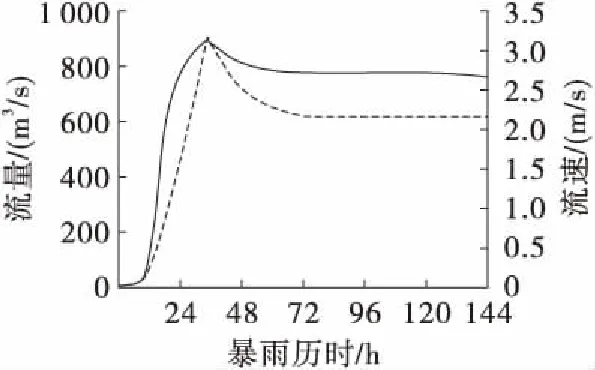
图7 溃决流量-决口流速过程曲线
由图7可知:溃决流量与流速的变化趋势一致,在溃决流量增大的同时决口处水流流速也急剧增大。并且,溃决流量达到最大的同时,决口处水流速度也达到最大值,峰值流速之后有所减小并逐渐趋于稳定。
通过溃决流量与决口水位、决口宽度及决口水流流速的过程曲线可以看出,上述模型模拟的河堤溃决过程符合河堤溃决的实际情况。
4 基于ArcGIS的河堤溃决风险分级
4.1 数据来源
为保证最终计算结果的精确性与真实性,必须尽可能采集研究区内的地形、地貌、土地利用情况等资料。对于地形、地貌情况等一般选用DEM数据来表现,土地利用类型等数据可从区域遥感影像上获取,本研究选用精度为30 m×30 m的DEM数据,DEM数据和遥感影像均来自地理空间数据云。数据在使用前应进行填洼处理等校对处理,剔除“伪地形”等所带来的影响。
4.2 分析原理
传统意义上的自然灾害风险表达式为[19]
风险=危险性×易损性 .
(10)
一般而言,灾害的危险性是研究的前提,承灾体的易损性是灾害的具体表现,风险则是研究结果。洪水灾害所造成的损失和危害在很大程度上取决于承灾体的承受能力,即经济效益的损失程度。受研究区范围限定,承灾体的易损性无法准确估算,且各区段差异基本可忽略,因此该方法的可行性受到了限制。
假设研究区内所有承灾体的易损性相同,转换思维研究洪水行进过程中由于下垫面所产生的水流摩阻损失,将洪水视为“承灾体”来求算洪水的“易损性”,用洪水行进路程及河堤距原承灾体的距离来估计下垫面对洪水的“危险性”,从而得出洪水的流损情况,进而对堤坝进行风险评估及分级。
4.3 ArcGIS区划分析
应用ArcGIS软件强大的空间分析功能,可以对研究区的洪水灾害危险性、易损性以及综合风险进行分析制图,能有效提高分析结果的精确性,减少不必要的人力、物力和时间上的消耗[20]。首先根据卫星图与遥感图进行匹配,选定研究区及附近范围,进行相应调整,再经ArcGIS软件操作得出新泰市土地分类图,如图8所示。由图8可知:人类居住区及植被覆盖区主要分布于河谷地带,建筑群和植被对洪水行进有较大的阻碍作用;裸岩、裸土区主要分布于近山体侧,研究区分布范围较少,且对洪水行进过程阻碍作用小。

图8 新泰市土地分类结果
根据校正处理过后的DEM数据,在ArcGIS软件中构建研究区的基本框架,从而确定区内的基本地形地貌情况,地形越高则表明对洪水行进过程的阻碍作用越大。其中地形标准差主要反映的是地形坡度变化,该值变化越大,对洪水的阻碍能力越弱。
土地分类图中包含有土地利用类型信息及地质信息,按表3中得到的权重对各影响因素进行赋值;根据研究区DEM分布情况,对各个不同区间的DEM进行赋值;由于监督管理因素在本模型中影响较小,故可忽略该因素的影响。为分析不同溃点对矿井的影响,首先假设洪水行进路线呈直线,计算洪水行进过程阻碍因子,则可得到不同溃点到矿井的阻碍因子总值。若阻碍因子总值越大,说明该溃点矿井危险越小;反之,则说明该溃点矿井危险越大。为计算方便,将研究区的堤坝分为7个区间段,根据得到的各影响因子权重、土地分类和DEM数据,通过ArcGIS软件进行计算,得到了如表4所示的各区间段路线阻碍因子总值。

表4 各区间段路线阻碍因子总值 ×10-3
根据各区段路线阻碍因子总值,将堤坝等级分为高风险区、较高风险区、中风险区、较低风险区、低风险区,最终得到研究区(图9)的堤坝风险区划图,如图10所示。

图9 研究区卫星遥感图
5 结 语
根据河堤决口处的流量、水位等水力参数建立了河堤决口预测模型,模拟分析了河堤溃决过程。根据ArcGIS软件建模计算得到了研究区堤坝风险区划分结果,可知第4区段矿井风险最大,而2007年山东新泰煤矿发生的矿井淹井事故堤坝决口点也在第4区段,说明该模型符合实际,对堤坝溃决预防工作有一定的指导意义。本研究的不足在于:①采用的数据精度不高,在结果处理上可能存在一些系统误差,与真实情况存在一定的偏差;②洪水灾害“危险性”评价指标过于单一,就理论而言强度指标应包括淹没水深、洪峰流速、洪峰流量、淹没历时等,但考虑到研究区范围受限等各种因素的影响,洪水准确的流速、持续时间等数据难于获取,本研究仅根据洪水溢流路程进行研究区洪水灾害“危险性”评价;③对洪水溢流过程中摩阻损耗的模拟分析采用的是静态模型,而实际情况可能复杂多样。
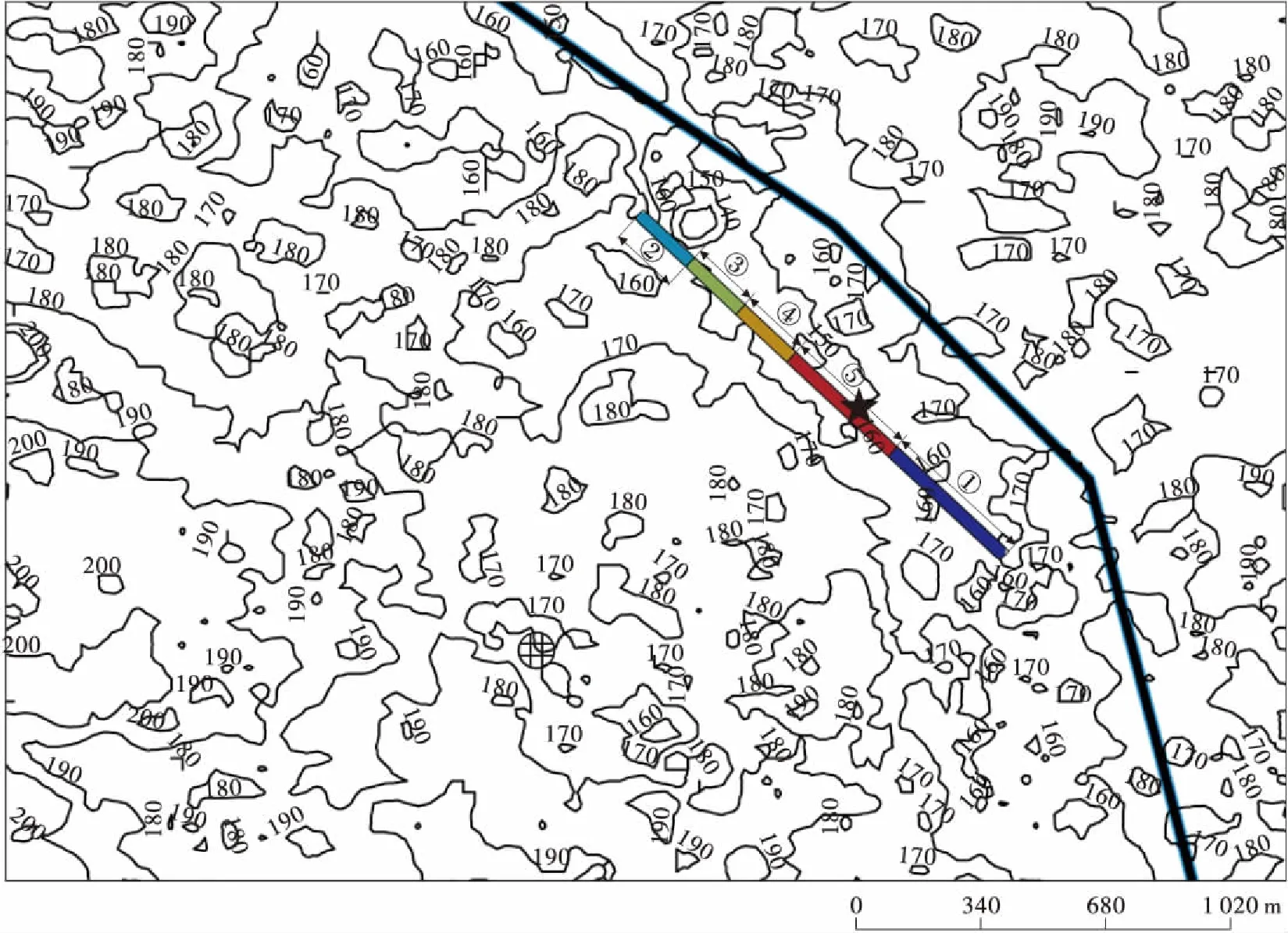
图10 研究区堤坝风险区划分结果(单位:m)

