拉格朗日乘子的解析与应用

(长江工程职业技术学院，武汉 430212)

众所周知，拉格朗日乘数法给出了求解多元函数条件极值的方法。以二元函数为例，函数z=fx,y在φx,y=0约束条件下的可能极值点x0,y0应满足：在该点，

(1)

(2)

(3)

1 乘子λ的意义

上述(1)(2)式中的λ，称为拉格朗日乘数法的乘子，它参与求解极值的运算，如果极值存在(以下不再说明)，则它本身的意义是什么？它的大小说明了什么？教材中一般不作解释。为解答这一问题，我们引入“约束参数”的概念。

在一个约束条件φx,y=0中，通常含有且只有一个反映约束程度的数量，表示为字母(例如A，此时，约束条件φx,y=0可改写为等价的ωx,y-A=0)。显然，函数的条件极值点x,y与函数的条件极值fx,y的取值，都受到这个数量A的制约，所以它们都是A的函数。为说话方便，称A为该约束条件的约束参数。(存在未显示约束参数的约束条件，将在例3中讨论)

例1：将周长为2p的矩形绕它的一边旋转而构成一个圆柱体，矩形的边长为多少时，可使圆柱体体积最大?

解：设矩形长、宽为a,b，则圆柱体体积V=fa,,b=πab2,且a+b=p.这里，p就是反映约束程度的约束参数。p

实际上，不仅约束条件和fx,y的极值是约束参数的函数，而且它们与拉格朗日乘子之间存在如下关系。

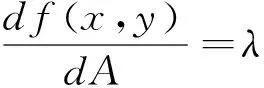
证: 由(1)(2)式，且因φx,y=0⟺ωx,y-A=0，所以φxx,y=ωxx,y,

φyx,y=ωyx,y,

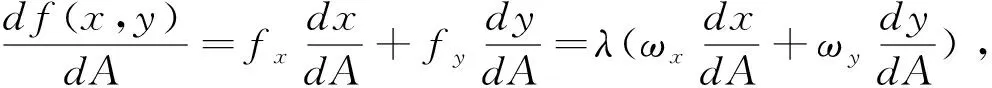
注意Δfx,y≈dfx,y=λdA,所以当dA=1,Δfx,y≈dfx,y=λ,即：当约束参数增加1个单位，条件极值近似地增加λ个单位。

续例1 (例1和下面的例3，其目的为便于说明定理一的应用，而非求条件极值本身。实际上若为后者，则将其化为无条件极值更简便。)

解: .由(1)，(2)，(3)式 ，最大体积矩形的应满足

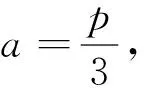
例2 ：设某种产品需要投入两种生产要素，x,y为两种要素的可投入量，其产出为u=fx,y，若资源总量为a，在满足φx,y=a的限制下，求最大的产出。

上式表明：乘子λ正是资源总量a对于最大产出的边际贡献，即此时若资源总量a再增加一个单位，则最大产出将近似地增加λ个单位。在经济学上，称λ为产出最大化时资源的影子价格，它为企业考虑是否增加生产提供了有用的参考。

2 约束条件多于一个的情形

当函数自变量多于两个，约束条件多于一个的情形，都有相应于定理一的定理。以4个自变量2个约束条件的情形为例。根据拉格朗日乘数法，u=fx,y,z,t在φx,y,z,t=0,ψx,y,z,t=0条件下的可能极值点x0,y0,z0,t0应满足：在该点，

(4)

(5)

必须注意这里有两个乘子λ1、λ2，分别称为第一，第二乘子，因为

φx,y,z,t=0⟺ωx,y,z,t-A1=0,

ψx,y,z,t=0⟺μx,y,z,t-A2=0

(6)

存在两个约束参数A1,A2分别称为第一、第二约束参数。由(6)式可得

φx=ωx,φy=ωy,φz=ωz,φt=ωt;ψx=μx,

ψy=μy,ψz=μz,ψt=μt

相应于定理一，有如下

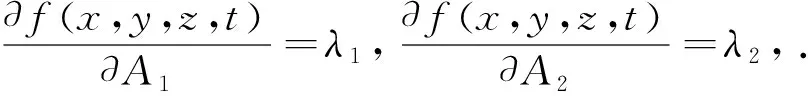
(7)

而由(5)式和(6)式

3 以一个已赋值的约束参数的例题来说明上述定理二

例3 某厂家生产一种产品，同时在两个市场销售，售价分别为p1和p2,销售量分别为q1和q2,需求函数为q1=24-0.2p1;q2=10-0.05p2,总成本函数为C=35+40q1+q2.厂家应如何确定两个市场的售价，使总利润最大，最大总利润为多少？

解:本题是求总利润fp1,p2,q1,q2=p1q1+p2q2-[35+40(q1+q2)]

在约束q1=24-0.2p1;q2=10-0.05p2下最大值的问题。两个约束表明：若价格p1,p2提高，则销售量q1,q2将减少,即后者受到前者的制约， 而24与10这两个数字，则表明了其制约的程度。即：若价格p1接近到24/0.2=120，则销售量q1将接近到0(对于10，情况类似)。由此可知，约束参数在这里被赋予了具体的数值24和10而没有显示，如果令其显示为A1,A2，则约束为q1=A1-0.2p1;q2=A2-0.05p2,

本题是四元函数两个约束条件的情况，由(4)，(6)式,可知: 使总利润最大的售价p1,p2应满足

经计算，得到p1=2.5A1+20,p2=10A2+20 此时，q1=0.5A1-4,q2=0.5A2-1。

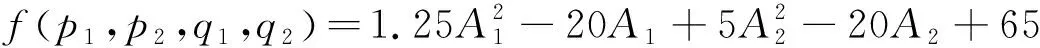
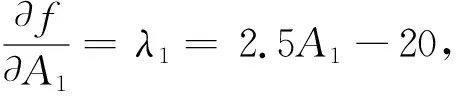
ΔA2=0(ΔA1=0),最大总利润将近似地增加λ1λ2个单位。

返回A1,A2的赋值，令A1=24，;A2=10，则p1=80,p2=120.q1=8;q2=4.

最大总利润f80,120,8,4=605.而λ1=40,表明若将A1增加一个单位，则产品在第一个市场销售量将增加，从而使最大总利润近似地增加40个单位 ，λ2=80的意义是类似的。若将A1，A2分别同时增加一个单位，则最大总利润将近似地增加λ1+λ2=120个单位。