基于多属性权衡空间探索的体系生存性分析
舒佳康 秦肖臻
近年来,军事和商业领域对由多个分散系统组成的空间系统的依赖性不断增加,使得体系(System of System,SoS),这一由众多地域分散,具备自治能力的组件系统集结而成的大型工程系统[1],越来越受到人们的关注.由于体系的组件系统,尤其是军事领域相关的组件系统,总是处于自然的或人为的扰动环境之中,这可能会导致体系总体性能的下降甚至体系崩溃,因此,体系生存能力的研究显得至关重要[2].
文献[3]在讨论空间系统的设计问题时,提出了生存能力的概念,以应对各种不确定性扰动的影响.文献[4]在文献[3]的基础上,对生存能力进行了更加深入的研究,将生存能力概念化为系统属性生存性,并将其纳入系统设计的早期阶段.文献[5]讨论了生存性的4个基本属性:容量、紧急门限、适应性和组件系统的协调程度.文献[6]指出了生存性的3个特点:降低易感性、降低脆弱性、增强恢复性.文献[7]提出了一种定量评估生存性的方法,并给出了生存性评估的指标,但这些指标都是离散的,二进制的,因而存在某些缺陷.文献[4,8]将时间概念引入生存性评估,指出生存性的动态、连续、相互依赖的本质.文献[9−10]在此基础上提出了两个动态连续的生存性指标,并列出了17个生存性设计原则,从多个维度来评估生存性.体系生存性是由组件系统之间以及组件与其所处环境之间的相互作用引起的应急系统属性,现有的大多数生存性分析方法通常基于具体的操作场景和预设的干扰,而不是具有不确定性扰动的一般理论,因此,本文介绍一种新的体系生存性分析方法—多属性权衡空间探索(Multi-attribute tradespace exploration,MATE),来定量评估体系生存性.
1 MATE方法及生存性概念介绍
MATE方法由麻省理工学院(MIT)的Adam Ross和Nathan Diller两位教授共同提出,这是一种将决策理论、建模和仿真相结合的方法[11],并且利用权衡空间探索来进行系统设计和设计方案的选择,因此,它既是一种解决问题的方案,又是一种决策分析的框架.
MATE方法的应用是一个从确定决策者到建立权衡空间的过程[12−13],如图1所示.该过程可以概括为4个阶段:引出属性、提出设计向量、创建权衡空间、评估备选方案.
第1阶段,确定决策者.由决策者的偏好引出系统属性,给出每个属性的效用函数,效用函数有正增益效用函数和负增益效用函数两类,如图2、图3所示,将属性值映射成效用值,并利用多属性效用理论,赋予每个属性一个权值,将它们集成为一个SoS效用函数:
第2阶段,分析属性.定义一系列设计变量及每个变量的范围,变量的范围一般为有限个离散值的集合.所有设计变量构成一个设计向量,设计向量的所有取值构成了设计空间,即备选方案集.
第3阶段,开发系统模型.将设计空间映射成权衡空间,即成本效用二维空间,如图4所示[13].
第4阶段,在权衡空间中每个点代表一个备选方案,可以运用帕累托分析方法来评价各个备选方案,得出非劣解[14].
生存性在物理上被定义为系统避免或承受自然和人为扰动而不会对其完成指定任务的能力产生毁灭性影响的能力.更一般的描述,在工程上生存性是系统将有限持续时间环境干扰的影响降至最低的能力.从过程的角度看,生存性是由系统与环境随着时间的相互作用而产生的,其本质是动态的,连续的,相互依赖的.文献[15−16]验证了体系生存性设计原则的正确性.文献[17]提出了一种生存能力分析框架来分析体系生存性.
2 体系生存性分析
目前,MATE在分析体系架构设计[11,18]、体系安全性[19]、体系韧性[20]等领域有着广泛的应用,有关MATE在体系生存性方面的研究也受到越来越多学者的关注,国内外已经发表了许多相关论文.
2.1 基于MATE的体系生存性分析
在权衡空间中,一个点代表一个具体的备选方案,每个备选方案的成本值在设计之初已经确定,是个定值.而效用值会受到扰动的影响,随着时间变化,如图5所示,即效用值是时间的函数,称为效用轨迹.
在效用轨迹中,有两个重要的门限值:紧急效用阈值和需求效用阈值.紧急效用阈值是组件系统受到扰动之后,决策者对体系效用值的最低可接受程度,通常将其设置为0 utils.需求效用阈值是系统在正常情况下决策者的期望值或者扰动过后系统恢复程度.
基于效用轨迹的两个门限值,可以将生存性分为3类,如图6所示.
扰动前,系统的初始效用值(效用是系统能力的数值化表示)为U0,如果在扰动持续时间内扰动不能使系统的效用U(t)降至需求效用阈值Ur以下,则认为系统的效用始终保持不变,等于初始效用U0,因而系统具有I型生存性;如果扰动使系统效用降至需求效用阈值Ur以下,但始终保持在紧急效用阈值Ue之上,并在扰动结束之后系统效能保持在Ue与Ur之间的某个值,则认为系统具有II型生存性;在II型生存性的基础之上,如果系统效用在扰动结束后的一段时间内恢复到了Ur之上,则认为系统具有III型生存性.在SoS系统中,体系各组件面对不同程度的扰动会表现出不同类型的生存性,因而分析体系整体的生存性往往需考虑3种生存性的综合.
2.2 体系生存性度量指标
通过对3种类型生存性的分析,可知其分别体现了体系在稳定性,抗损失能力,恢复能力等3方面的性能,由此提出生存性的度量指标.
1)稳定性指标其中,AT表示体系效用值在需求效用阈值之上的总时间,Tdl表示运行周期.PS反应了体系在稳定性方面的能力,PS越大,体系的稳定性越强,生存性也就越大.
2)抗损失能力指标
其中,U(t)表示体系效用函数,Ur表示需求效用阈值,Ue表示紧急效用阈值,Tdl表示体系运行周期.若体系效用的平均值小于紧急效用阈值,即则令PL=0;若体系效用的平均值大于需求效用阈值,即则令PL=1.PL反应了体系在抗损失方面的能力,PL越大,体系抗损失能力越强,生存性也就越大.
3)恢复能力指标
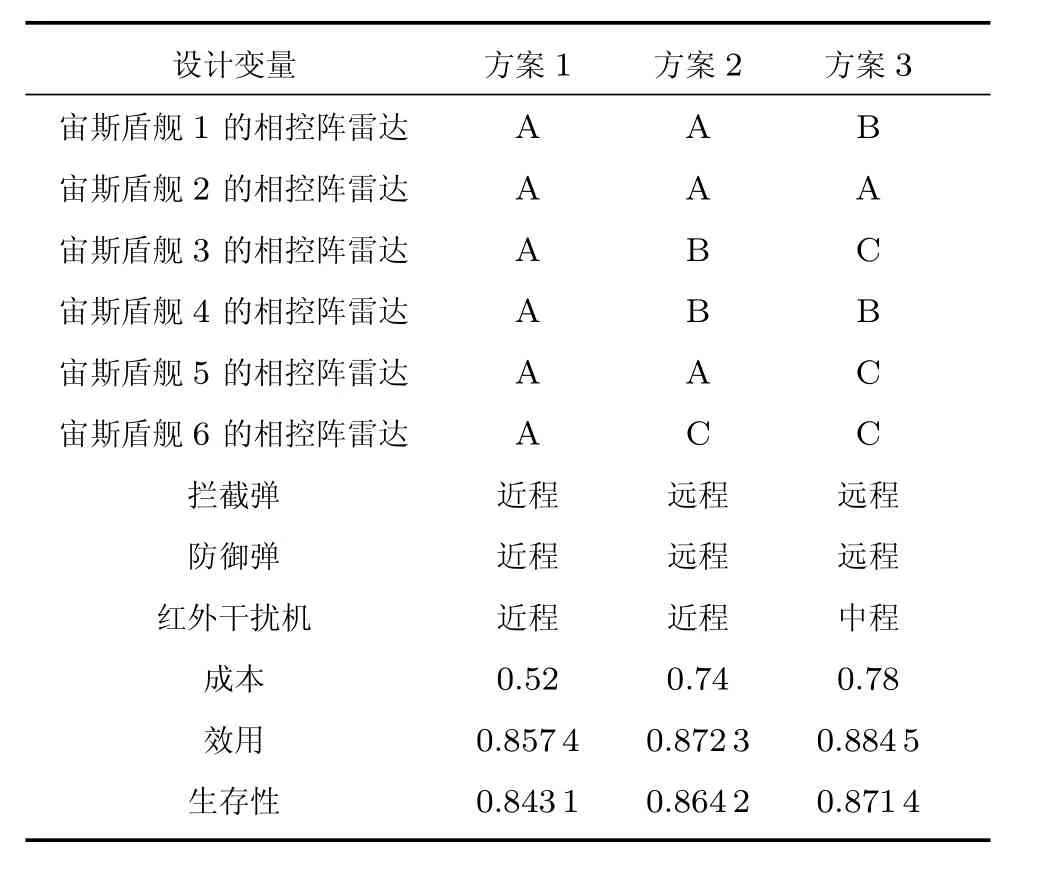
其中,t表示体系开始受到干扰的时间,Tr表示允许恢复时间,Ur表示需求效用阈值,Ue表示紧急效用阈值.若体系在允许恢复时间内没有达到紧急效用阈值,即U(t+Tr) 4)生存率 其中,Ts表示效用轨迹在紧急效用阈值之上的时间,η的值在0∼1之间. 综上所述,生存性的评价指标可定义为:Psur=(w1PS+w2PL+w3PR)•η,且w1+w2+w3=1. 之前介绍了传统MATE方法,但在实际运用过程中需要根据具体情况来改进该方法.在分析体系生存性时,由于要考虑扰动的影响,需要根据扰动来增加必要的生存性变量,因此,需要对MATE方法进行改进,如图7所示.加入了生存性后,权衡空间由二维的效用-成本变成三维的效用-成本-生存性.在三维空间中仍然需要找到帕累托前沿,然后根据决策者需求寻找非劣的备选方案.道进行拦截.根据想定,提出系统的属性.传感器系统有4个属性,分别是目标获取时间、目标跟踪时长、探测范围和探测概率.武器系统有两个属性,分别是目标识别概率和拦截概率.这些属性对应的效用函数如图8所示. 弹道导弹防御系统(Ballistic Missile Defense System,BMDS)是一个典型的SoS,它由传感器系统、武器系统和指挥控制系统等分系统组成.传感器系统主要由预警卫星、多功能雷达等组成,完成发现、搜索、跟踪等功能;武器系统包括宙斯盾舰、SM-3拦截弹等,主要任务是识别目标,并对弹道导弹进行拦截和摧毁;指挥控制系统是整个BMDS的核心,负责各分系统的通信,传递作战信息和发布作战命令.以BMDS为例,运用改进的MATE方法来分析体系的生存性. 根据BMDS的作战任务和作战流程,想定BMDS部署有6艘宙斯盾舰,并对一条特定的弹 根据上述提出的属性,得出对应的设计变量分别是每艘宙斯盾舰的相控阵雷达的类型和拦截弹的类型.如表1所示. 表1 设计变量 BMDS是一个陆海空一体化的防御作战系统,其受到的威胁可能来自各个方面,由于宙斯盾舰在BMDS系统中的重要性,其生存能力必须得到重视,基于此考虑,本文想定的干扰主要来自海上的鱼雷、舰艇和来自空中的红外干扰弹,所以,增加了防御弹和红外干扰机两个设计变量,分别有近程防御,中程防御和远程防御3种类型. 综合前面提出的设计变量,一共有9个设计变量,每个变量有3个取值范围,所以一共有19701种设计方案.开发相应的模型,计算每个设计方案的成本、效用和生存性,构成体系效用评估的权衡空间.由于有些设计方案的效用值会低于紧急效用阈值,故在生成权衡空间时直接将这些方案舍去,如图9所示. 权衡空间中红色的点代表位于帕累托前沿的设计方案,选取位于该区域的3个设计方案进行比较,比较结果如表2所示. 由表2可知,设计方案所有的设计变量均取最小值时,体系效用和生存性最低,不能满足决策者的期望,也不能保证系统安全有效地运行.适当增加系统设计的投入成本,增加系统各组件的能力,以此增加体系的整体效用.此外,对系统抗干扰能力的增强,除了会使体系整体效用得到提升,还会大大增加体系的生存能力. 表2 3个备选方案生存性比较 本文将MATE应用于体系生存性分析,并依据生存性准则,对传统的MATE方法进行改进.在原有基础上,考虑扰动的影响,增加扰动变量的分析,运用该方法更精确地评价体系生存性.根据体系生存性的稳定、抗损、恢复3方面的性能,提出了生存性的综合评价指标,作为体系生存性分析的依据,并将其纳入权衡空间,构成“成本–效用–生存性”三维权衡空间,全面而直观地分析生存性.本文为体系结构设计和体系生存性分析提供了参考,下一步,将会研究如何减少权衡空间中的备选方案的个数,以及如何更方便更全面地在权衡空间中寻找非劣解,以改善MATE方法在方案比较中存在的局限性.2.3 改进的MATE方法
3 示例分析

4 结论

