基于高光谱的干旱区盐渍化土壤盐分含量估算

如则麦麦提·米吉提， 买买提·沙吾提， 麦尔耶姆·亚森， 马春玥

(新疆大学资源与环境科学学院/新疆大学绿洲生态教育部重点实验室，新疆乌鲁木齐 830046)

土壤盐渍化是土地退化的主要表现，灌溉引起的土壤次生盐渍化成为限制干旱区农业经济发展的因素之一，也是影响绿洲生态环境稳定与安全的重要因素[1]。盐渍土是重要的耕地后备资源，及时获取土壤盐渍化信息，对于我国西北部干旱区的可持续发展至关重要[2-3]。遥感技术能宏观、快速地提取地表时空信息，已成为动态监测土壤盐渍化的新方法[4]。盐渍化土壤的光谱反射特征是由土壤理化性质决定的，传统遥感数据并不能完全反映土壤的光谱特征，而高光谱数据能够提供盐渍化土壤细微的光谱特征。光谱分辨率高、波段具有连续性强、光谱信息量大的优点。阐明土壤属性与其高光谱的关系，成为高光谱遥感技术定量监测和提取土壤信息的重要方法，为实现大尺度、实时监测土壤提供了新途径，使定量反演土壤盐渍化状况成为可能[5-12]。目前，国内外己有众多学者对土壤盐渍化的高光谱特征及定量、半定量做了大量的研究工作，Dehaan等观测澳大利亚Murray-Darling盆地的盐壳及重度、中度、轻度盐渍土的光谱，发现这4类土壤在不同光谱波段有明显的吸收作用[13]；Leone等应用实验室光谱进行多元统计分析以评价土壤开发和土壤退化程度并建立预测模型[14-16]。刘庆生等分析了盐分含量与上覆植被光谱的关系[17]。马诺等通过野外调查以及实地测点，利用便携式光谱仪测量研究区域内不同盐渍程度的土壤光谱，分析土壤光谱曲线与土壤盐渍程度之间的关系[18]。刘亚秋等利用热红外光谱仪建立了盐分与盐渍化土壤发射率一阶导数模型[19]。彭杰等对野外高光谱数据与土壤含盐量进行耦合分析并建立多元线性回归建模，决定系数达到0.80[20]。丁建丽等利用高光谱数据建立的监测模型为提取盐渍化土壤信息提供了依据[21]。

基于此，本研究以新疆维吾尔自治区渭干河-库车河三角洲绿洲为研究区，利用57个表层土壤样品的室内高光谱数据，并结合实测土壤含盐量，研究15种数学变换处理在高光谱数据估算荒漠土壤含盐量的可能性，并应用偏最小二乘回归、主成分回归、多元逐步线性回归建立土壤含盐量估算模型，以期为干旱区绿洲土壤盐渍化的高精度遥感监测提供一种更为有效的手段。

1 材料与方法

1.1 研究区概况

胃干河-库车河流域简称胃-库绿洲，是位于我国西北部的典型干旱区绿洲。本地区行政上辖阿克苏地区的库车县、沙雅县、新河县，地理坐标分别为80°37′～83°59′E，41°06′～41°40′N。绿洲北部跟天山南部接壤，南部延伸到塔克拉玛干沙漠北缘。胃-库绿洲是胃干河-库车河长期沉淀形成的山前冲洪积扇平原，是塔里木盆地的主要绿洲及我国重要的产棉区之一。该绿洲位于中纬度地区，远离海洋，气候干燥，风沙频繁，降水稀少，蒸发量大，昼夜温差大，夏季干热，冬季干冷。年均气温10.5～11.4 ℃，年降水50.5～66.5 mm，年均蒸发量2 000.7～2 092.0 mm，年均无霜期 240 d。土壤以轻壤和沙壤为最多，中壤、重壤、黏土有少量分布，土壤构成物颗粒细，透水性差。

1.2 数据采集

本研究于2016年4月中旬，在渭干河-库车河绿洲进行野外调查，采集57个采样点的土壤样品，采样点分布见图1。每个点分3层取样(0～10 cm、10～30 cm、30～50 cm)，共采集171个土样。样品在室内条件下自然风干，磨碎后过2 mm筛子。其中，每个样品分为2份，1份样品用于测定土壤，盐分、溶解性固体(TDS)、pH值等指标，另1份用于土壤光谱的测定。在土水体积比为1 ∶5的土壤悬浊液中，使用便携式多参数分析仪Multi 3420 SETB(wissens chaftlich technische werkstätten，德国)进行指标测定。

测出的土壤参数值统计特征见表1。本研究区含盐量最大值为69.8 g/kg，最小值为0 g/kg，平均值为20.19 g/kg，变异系数为99.15%，属强变异，表明土壤盐分分布很不均匀。土壤样本的pH值变异系数为8.26%，属低变异。根据土壤的分级标准，57个样本中，非盐渍土样本为13个，轻、中、重度盐渍化样本数分别为11、10、23个。非盐渍化土壤样本主要以绿洲内部为主，内部到绿洲与荒漠边界土壤含盐量逐渐增加。中、重度盐渍化土壤分布在研究区的东南部区域。

表1 土壤指标统计特征

注：样本数=171个。

表2 土壤盐渍化程度分级标准[22]

1.3 土壤样本光谱测定

使用FieldSpec3型光谱仪(analytical spectral devices)，波段范围为350～2 500 nm，光谱采样间隔分别为 1.4 nm(波段350～1 000 nm区间)和2 nm(波段1 000～2 500 nm区间)，采样间隔为1 nm，输出波段数为2 151个。土壤样本光谱测定在能控制光照条件的暗室内进行，测试之前都要进行白板校正，仪器光源为50 W卤素灯，天顶角为15°，8°视场角探头垂直土样表面，距离为10 cm。每个土样分别测10次，并取其算术平均值作为该样品的实际光谱反射率。

1.4 数据预处理与变换

将57个采样点的表层土壤含盐量从高到低进行排序，等间隔选取37个作为建模集，20个作为验证集，分别用于模型的建立以及精度验证。将通过显著性检验(P<0.01)的波段作为自变量，利用偏最小二乘回归法(Partial Least-Squares Regression，PLSR)、主成分回归模型(Principle Component Regression model，PCM)和多元逐步回归模型(Multiple Stepwise Regression Model，MSRM)建立土壤含盐量的估算模型，通过对比各模型的决定系数(Determination of Coefficients，R2)、均方根误差(Root Mean Square Error of Prediction，RMSE)、相对分析误差(Relative Prediction Deviation，RPD)筛选出最优模型。R2用于判定模型的稳定程度，取值范围为 0～1，其值越大说明该模型的稳定性越好；RMSE用于表征模型的准确性，其值越小，表明模型的精度越高。另外，当RPD的值小于1.4时，模型基本上可用；当RPD的值在1.4～2.0之间时，模型估算精度一般，RPD值越大于2.0，表明模型的定量预测能力越好[25]。

2 结果与分析

2.1 土壤样本反射光谱曲线特征

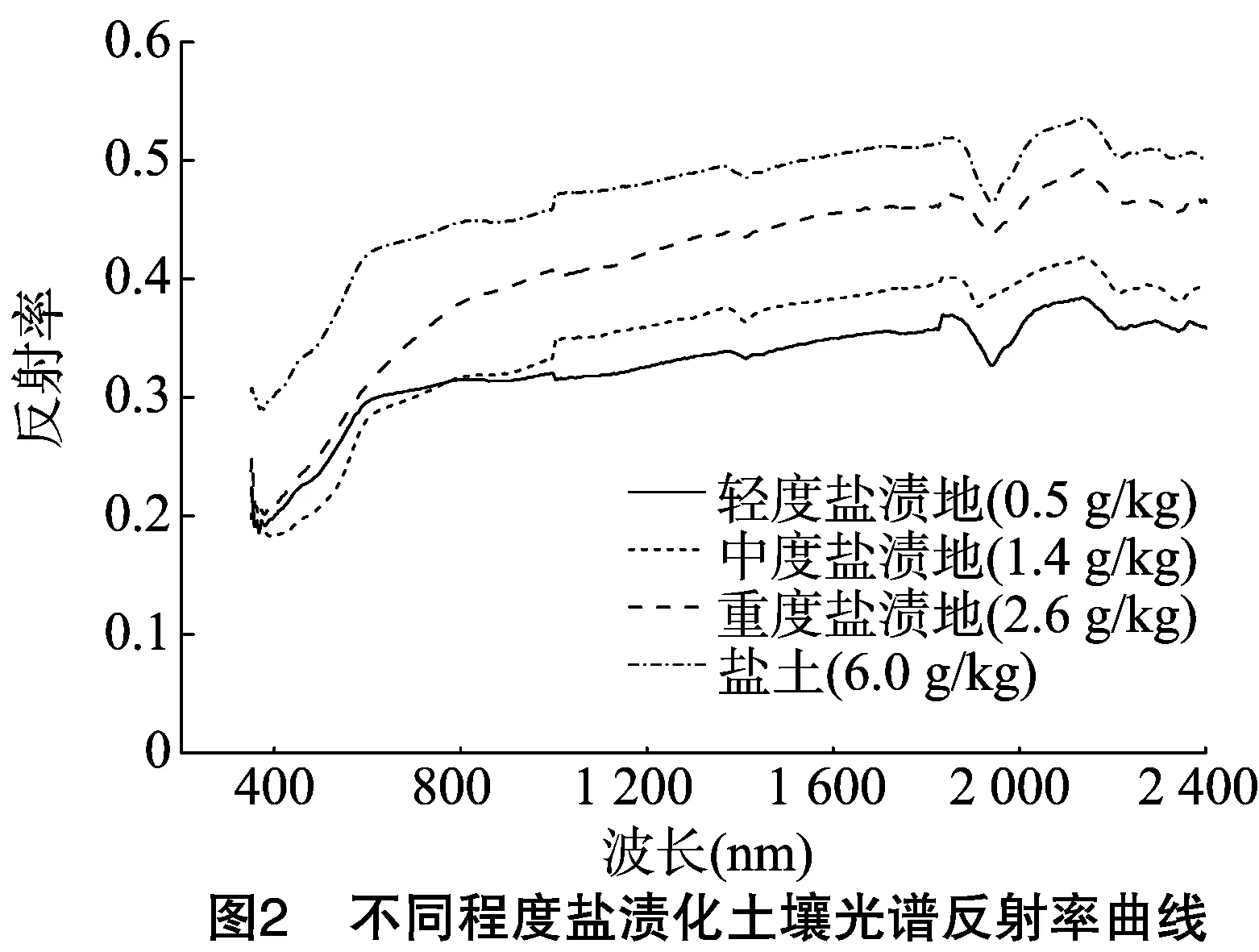
将57个土壤表层样本反射率以土壤盐渍化程度分级标准进行分类再求平均，作为不同程度盐渍化土壤样本的光谱反射率曲线。从图2可以看出，4条曲线变化趋势大致相似，土壤光谱从350～1 300 nm内波段范围持续上升，至 1 400 nm 处出现一个浅水分吸收谷，之后从1 400～1 850 nm波段范围内继续升高，但增加幅度较为平缓，至1 900 nm处再次出现一个深的水分吸收谷。土壤成分含量值在一定程度上决定了土壤光谱曲线反射率值的大小和曲线整体的走势，含盐量越高，反射率也高。

2.2 土壤含盐量与光谱相关性分析

将土壤含盐量与光谱反射率及其15种变换形式做相关系数在0.01水平上的显著性检验及相关性分析。从图3可以看出，从土壤含盐量与光谱的相关性分析来看，反射率一阶微分(图3-b)、反射率二阶微分(图3-c)、对数相反数一阶微分(图3-i)、连续统去除一阶微分(图3-o)、平方根一阶微分(图3-m)、立方根一阶微分(图3-k)与土壤含盐量数据的整体相关系数较好，并通过显著性检验(P<0.01)。土壤含盐量与R、1/R、(1/R)′、lgR、1/lgR、连续统去除法、反射率平方根、立方根的相关性较小，没有通过0.01水平显著性检验的波段。因此，从光谱反射率及其15种变换形式中，遴选出以上5种，只对以上5种光谱反射率变换结果分别与土壤含盐量进行估算模型的建立与验证。

结果表明，单个波段所建立的模型很难预测土壤含盐量，微分变换较好地体现了原始数据中隐晦的光谱信息，相关性得以提升，据此运用光低阶微分处理方法，可以筛选出对土壤含盐量敏感的特征光谱波段[26]。光谱反射率不同变换形式与土壤含盐量特征波段的选取是选择相关系数的峰值所对应的光谱波段。

2.3 土壤含盐量建模

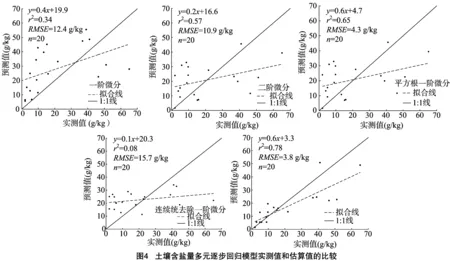
根据以上相关分析结果得到的特征光谱波段，针对本研究的高光谱指数分别建立土壤含盐量的偏最小二乘回归模型，主成分回归模型和多元逐步线性回归模型。DPS数据处理软件将57个土壤样本中随机选取的37个样本用于建立模型，以土壤含盐量作为因变量，以特征波段的光谱反射率作为自变量，分别建立土壤含盐量的偏最小二乘回归模型、主成分回归模型和多元逐步线性回归模型。运用偏最小二乘回归模型见表3，主成分回归模型和多元逐步线性回归方法的敏感光谱波段与土壤含盐量之间的预测模型。从表3可以看出，以原始光谱与土壤含盐量相关性较差，相关性最大的不到 0.2，没有超过0.01显著性检验线，因此建立的模型拟合精度很差。经过微分变换后，土壤含盐量与高光谱的相关性有所提高，最大可达到0.47，为挖掘敏感波段呈现良好的效果，建立的模型估算精度较好。所选择的5种数学变换形式当中，基于连续统去除一阶微分模型的决定系数最差，立方根一阶微分的最好。根据决定系数R2和相对分析误差RPD值最大、均方根误差最小的原则，对于各种变换形式，3种预测模型都是土壤含盐量立方根一阶微分光谱特征波段为自变量时拟合最优，R2值分别为0.68、0.65、0.85。利用多元逐步线性回归方法建立的模型的精度最高，模型的R2、RPD和RMSE分别达到0.85、2.36、1.8。可以使用这种预测模型来定量反演土壤含盐量，提取土壤盐渍化信息。

表3 含盐量回归模型

2.4 模型精度检验

根据模型的精度参数，对建立的模型进行筛选后发现，RPD≥2的模型只有2个，是基于平方根一阶微分和立方根一阶微分的多元逐步线性回归模型建立的模型，其他模型的RPD属于小于或等于1.5。对模型的R2、RMSE、RPD以及波段数量进行综合对比发现，基于平方根一阶微分和立方根一阶微分建立多元逐步回归模型RPD、RMSE、R2最优且参与建模的波段数量较多(19个和16个)。一阶和二阶微分模型对验证样品的含盐量决定系数分别为0.34和 0.57，偏离1 ∶1线，模型估算精度不高。连续统去除一阶微分模型对验证样品的含盐量决定系数最差，只达到0.08。对3种建模方法而言，基于多元逐步线性回归方法的模型精度高于其他2个方法的建模精度；利用主成分回归方法建立的模型精度最低，R2值最高到0.68。对原数据的数学变换后整数阶微分而言，一阶微分处理增强了原数据的敏感性及建模能力。说明原始数据的平方根一阶微分和立方根一阶微分一定程度上可以增强光谱对含盐量的敏感程度，并利用多元逐步线性回归方法对估算土壤盐含量具有较好的定量反演能力，且计算量相对较小，因而确定该模型为最优模型(图4)。

3 结论

在本研究中，通过对土壤含盐量与高光谱指数之间的相关性分析、3种预测模型的建立以及模型精度验证，可以得出以下结论。

在不同盐渍化水平下，土壤的光谱特征在形态上趋于一致；在整个波谱区间，土壤的光谱反射率随盐渍化程度的加重呈现增加趋势。

对原始高光谱数据的15种数学变换中，利用微分处理是体现光谱数据敏感波段效率好，经微分变换后的高光谱指数与土壤含盐量进行相关性分析，筛选出对土壤含盐量变化响应的敏感波段，构建基于偏最小二乘回归、主成分回归和多元逐步线性回归的土壤盐分监测模型。结果表明，立方根一阶微分变换形式为构建预测模型的最佳光谱指标。

对土壤含盐量的3种回归模型预测效果进行检验，比较实测值与预测值的相关关系。结果表明，多元逐步线性回归模型的稳定性和预测精度高于其他2种回归模型，证明了该方法的普适性。

本研究运用偏最小二乘回归、主成分回归和多元逐步线性回归模型在实验室内对干旱区土壤盐分含量的测定，对比3种回归方法所建立模型的精度，发现多元逐步线性回归模型的预测精度最高。但影响土壤光谱反射率是土壤的粒径、粗糙度和水分含量等多种因素的综合反映。在今后的研究中要考虑这些因素的影响。