基于幂指数法的通信系统基础能力模型研究
罗颖光,邹自力,袁荣召
(国防科技大学信息通信学院,武汉 430010)
0 引言
为进一步提升训练水平和训练效果,全军部队和院校广泛开展了模拟化、网络化指挥对抗训练。通信系统作为联合作战通信保障力量的核心,是网络信息体系对抗作战中不可或缺的重要因素[1]。在作战阶段,如何科学量化通信兵力和通信装备效能,对于合成指挥员实时掌握通信系统的整体情况起着至关重要的作用。作为合成指挥员,并不需要实时掌握每一套通信装备和每一员通信兵力的具体情况,只需要从整体上掌握通信力量的整体效能即可。本文基于指挥对抗模拟训练,着眼合成指挥员对通信系统的“特殊”需求,利用“幂指数法”构建通信系统基础能力模型,可为合成指挥员从整体上掌握通信力量效能提供手段支撑。
1 基础能力结构
1.1 基础能力
实际作战中,通信兵力和通信装备是通信力量的主体,决定着战场中的通信保障效能,故本文从通信装备能力和通信兵力能力两个方面对基础能力进行建模。
1.2 通信装备能力
通信装备是保障信息通信任务的基础和载体,是通信保障能力比较重要的因素,通信装备能力体系是通信装备能力模型具体构建的依据,因此,如何科学合理建立通信装备能力体系尤为重要。通信力量包括的通信装备种类繁多、型号各异、功能不一。例如:从通信装备的功能上可以区分为传输设备、终端设备、交换设备和用户设备,从通信装备的信息传输手段上可以区分为无线电通信设备、有线电通信设备。通信装备能力重点描述参与通信保障任务的通信装备的基本性能,考虑到通信装备能力模型性能需要和研究实际,可将通信装备分为无线电设备和有线电设备来进行研究[2]。
在装备性能参数的选取上,通信装备的性能参数较多,如无线电通信装备常见的性能参数有:接收和发送的频率范围、业务类型、通信距离、通信容量、连续工作时间、功率、尺寸、重量等。为进一步增强通信装备能力模型的实用性和快捷计算的能力,在对通信装备的性能参数分析上遵循以下几个要求:
1)便于具体对通信装备性能参数有足够的敏感性(能够真实反映装备性能且具有足够的灵敏度);
2)能够反映通信装备完成保障任务真实程度;
3)物理意义明显,便于数据采集。
根据上述3项装备参数选取要求,通过聚类分析通信装备性能参数,分别选取无线电和有线电通信设备的6个性能参数参与模型的计算。其中,无线电通信设备主要的性能参数是通信距离、通信容量、业务类型、传输速率、信道数及信道利用率;有线电通信设备的性能参数是传输距离、传输容量、工作种类、波道数及波道利用率,如图1所示。
1.3 通信兵力能力
通信兵力能力一般情况下从通信人员的编配情况、训练水平和科学文化水平3个方面考虑。但是考虑到在指挥对抗模拟训练系统中,通常情况下都是人机结合使用,因此,本文只将通信兵力能力作为影响因子使用,不再单独分析。
2 基础能力建模
由于通信兵力能力可以能力因子的形式对基础能力施加影响,因此,计算通信装备能力是通信系统基础能力模型计算的重点。计算通信装备能力,可以先计算单装通信能力,再计算各类型的通信装备能力,最后聚合为通信装备能力。然后通信装备能力和通信兵力能力因子再有机结合,构成通信装备的基础能力。
2.1 通信装备能力模型
由通信装备能力体系结构可知,通信装备可分为无线电通信装备和有线电通信装备两大类,共12项性能参数,均可以通过直接读取或测量获得。根据幂指数法原理[3],将各项性能参数规范化处理后,即可得出单个无线电通信设备和有线电通信设备的能力指数。
2.1.1 单个无线电通信设备能力指数
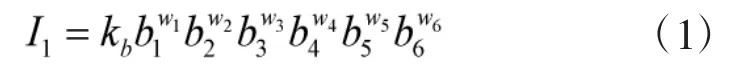
式中,I1为无线电通信设备能力指数;bi为第i种无线设备性能参数(经规范化处理);wi为第i种性能参数对于无线电设备的权重,wi满足下面的关系:

2.1.2 单个有线电通信设备能力指数
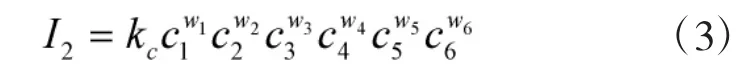
式中:I2为有线电通信设备能力指数;ci为第i种有线设备性能参数(经规范化处理);wi为第i种性能参数对于有线电设备的权重,wi满足下面的关系:

具体计算过程中,通信装备性能参数规范化处理主要包括无量纲处理和归一化处理。单装能力指数计算后,对于同类的通信装备,只进行数量叠加即可,而对异类通信装备进行数量处理时,不能简单地相加,这样容易造成大量劣势通信装备的能力指数超过少数优势通信装备的能力指数。参考兰彻斯特方程线性律和平方律思想,为客观描述每一种通信装备能力在整体通信装备性能中的所占比例,引入折合幂因子进行数量处理[4]。
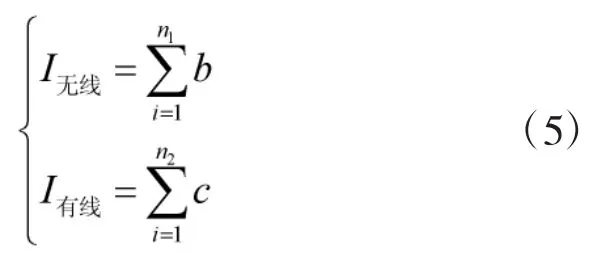
式中,I无线,I有线分别表示所有无线电、有线电通信设备的能力指数,n1,n2分别表示无线电、有线电通信设备的数量,b,c分别表示无线电、有线电通信设备的单装能力指数。
引入折合幂因子后,通信装备能力指数模型为:
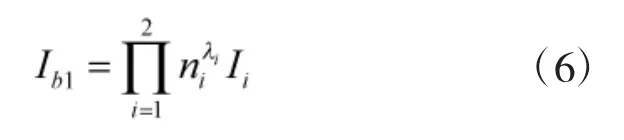
式中,Ib1为总的通信装备能力指数,ni为i类通信装备的数量,i为i类通信装备的折合幂因子,Ii为第i个类型通信装备能力指数。
2.2 通信兵力能力调整因子
指挥对抗模拟训练中,仿真运行时通常认为人装一体,对于通信力量的考虑重点集中在通信装备的数量、性能等方面。但通信装备效能发挥的关键作用还是人的因素。因此,通信保障基础能力模型中需要引入通信兵力能力因子 η,η∈[0,1],为切实描述指挥对抗模拟训练中人装一体的能力,具体训练中可根据需要进行设置取不同值来体现差异性。
2.3 基础能力聚合模型
通信装备能力模型建立和通信兵力影响因子确定后,为更加逼真模拟实战中的通信装备损伤和通信兵力损伤情况,引入通信装备损伤系数α和通信兵力损伤系数β引入到基础能力模型中。
据此,可得通信系统基础能力指数
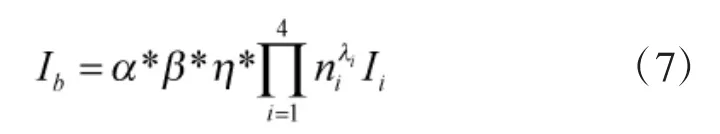
式中,Ib为通信保障基础能力指数,α为通信装备损伤系数,β为通信兵力损伤系数,η为通信兵力能力因子,ni为i类通信装备的数量,i为i类通信装备的折合幂因子,Ii为第i类单装通信装备能力指数。
由此,可知基础能力模型的计算流程,如图2所示。
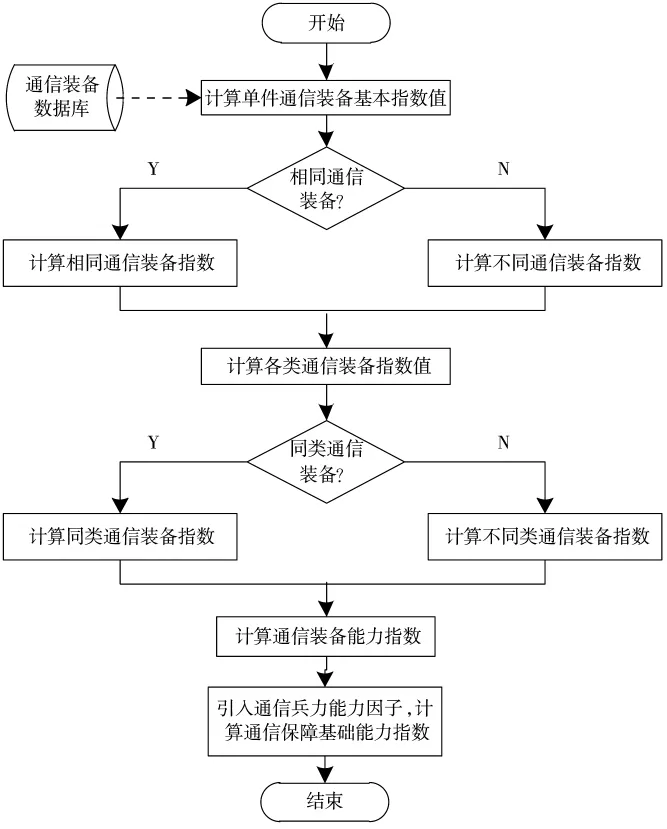
图2 基础能力指数计算流程
由图2可知,基础能力指数的计算流程为:读取通信装备数据库,计算单个通信装备能力指数,计算各类通信装备能力指数,最后两类通信装备聚合后引入通信兵力能力因子,计算基础能力指数。
3 算例与分析
从基础能力模型可以看出,通信装备的12项性能参数可以通过直接从通信保障方案或者实际装备性能参数得到,实际需要计算的是各性能参数的权重,这里使用层次分析法[5]可以获得各性能参数的权重。
3.1 权重计算
在能力体系中,各项能力相对于上层能力的重要程度是不同的,当权衡各项能力对其上层能力的贡献时,应赋予不同的权重。基本步骤为:
1)构造两两判断矩阵,首先进行专家咨询,然后利用层次分析法造两两比较判断矩阵。
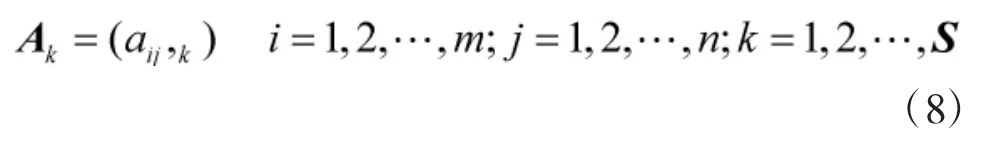
将S个判决矩阵,用加权几何平均的方法获得一个综合判决矩阵。
式(8)中的aij通过下式计算得到:
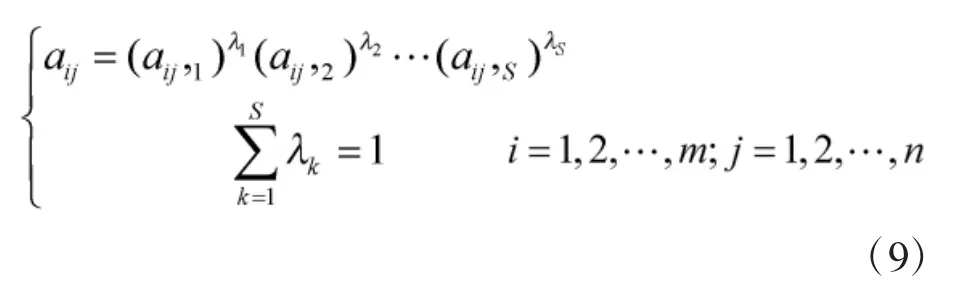
2)确定各层能力的权重。
采用乘积方根法计算权重,公式如下:
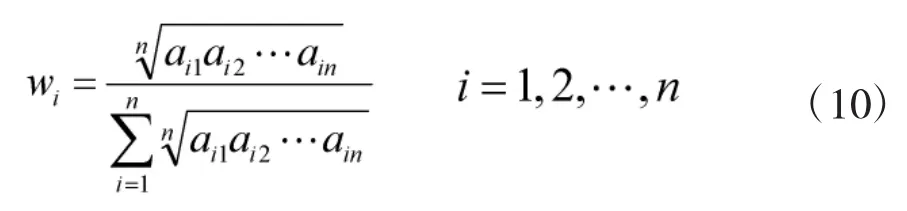
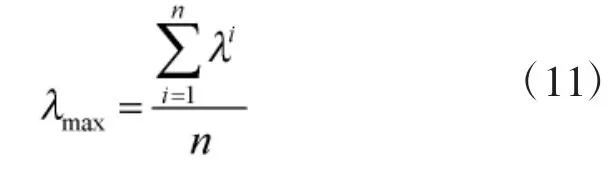
其中:
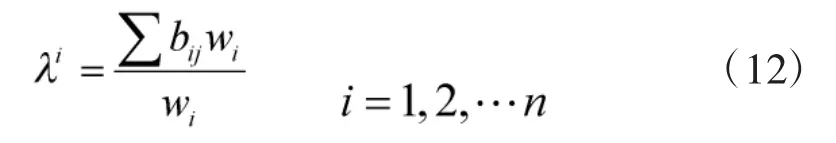
4)判决矩阵一致性检验。
若CR<0.1,认为判决矩阵的一致性是可以接受的;否则,应对判决矩阵进行适当修改。
以下是6名专家参与评估的通信装备能力的权判断矩阵。
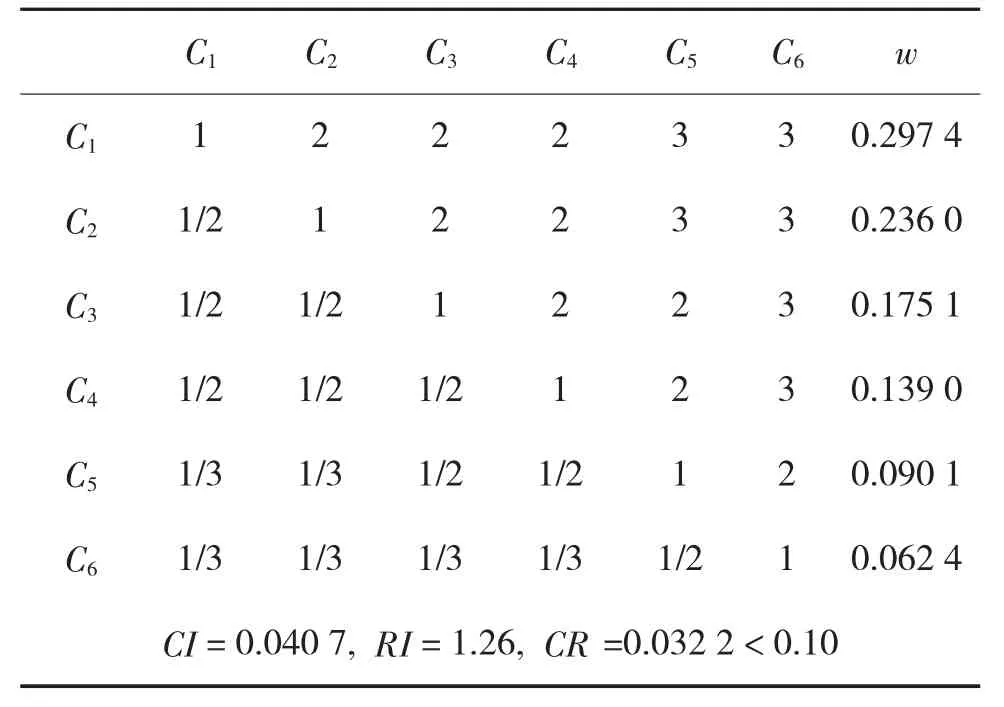
表1 通信装备能力因素判断矩阵
3.2 仿真实现
各能力因素权重确定后,经过读取通信保障方案中通信力量的编制、通信装备的种类数量和性能参数,便可以对通信基础能力进行计算。为简化计算,通信装备的折合幂因子均设置为1,通信兵力能力因子设置为0.9。由此,可以计算得出通信系统基础能力指数初始值为550。随着指挥对抗模拟训练时间推进至4 h,通信系统基础能力指数下降至200。
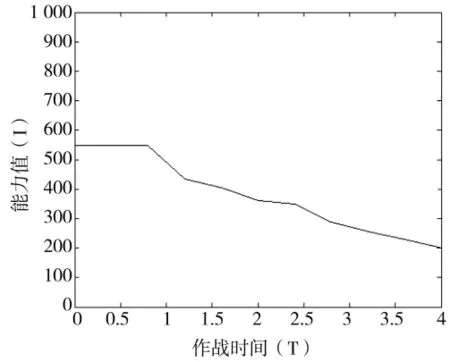
图3 基础能力变化曲线图
由图3可以看出,基础能力指数随着作战时间向前推进呈下降趋势,一方面是由于随着作战时间向前推进,我方通信装备受到敌方的硬摧毁和软打击,通信装备一定程度上受损;另一方面是随着作战时间推进,我方和敌方使用了较多的用频装备,致使战场电磁频谱环境变得较复杂,导致我方部分通信装备的通信性能下降。
4 结论
科学准确地掌握通信系统的整体情况对于合成指挥员及时处置战场情况至关重要。本文围绕指挥对抗模拟训练中合成指挥员对于通信系统基础能力的需求,根据通信系统的构成要素,从通信兵力和通信装备两个方面详细设计了模型的体系结构,为全面构建通信系统基础通信能力模型奠定了基础;采用聚合思路,基于幂指数法构建了通信系统基础通信能力模型,利用层次分析法计算了模型中性能参数权重,通过算例进行了模型验证,收到较好的效果,对促进指挥对抗模拟训练具有一定指导意义。

