基于扰动补偿自适应的Hexapod微激励系统低频振动控制
沈靖豪,黄 海,张 泽
(1.北京航空航天大学 宇航学院,北京 100191; 2.贵州大学 机械工程学院,贵阳 550025)
0 引言
空间飞行器在轨运行期间会产生难以避免的微振动,虽然该振动幅值很小,对精密设备的影响却是极其显著的。为了研究微振动对航天器上有效载荷的影响以及验证相应隔振系统的有效性和可靠性,需要设计微激励设备来模拟空间环境中的微振动。Hexapod平台是一种六自由度并联机构[1],能够同时产生六自由度的振动激励,具有定位精度高、刚度大、结构稳定、承载能力强、自身惯量小、动态特性好等特点,可以模拟复杂振动环境,被广泛应用于各类振动试验设备设计中,如美国空军实验室的高频振动台[2]及MTS公司的Model 353[3]振动台。
如何有效控制Hexapod平台产生期望的振动信号一直是研究的重点。文献[4]提到的三参量(位移、速度和加速度)控制是多自由度振动台控制器中最常见的控制算法,但在应用时需要对其中的6个参数反复手动调节,致使控制效率低下;文献[5]指出在基于动力学的控制方法中,六自由度运动平台的动力学模型精度很重要,而实际系统往往难以精确建模,由此引入的模型误差降低了控制精度;文献[6]针对Hexapod平台中非线性特性引起的谐波失真提出的自适应谐波消除算法,必须根据实验结果中所有的谐波频率来对应设计每一个频率的谐波消除器,故当谐波频率繁杂时难以取得理想效果。
为有效解决以上问题,本文基于自适应控制,针对其稳定条件,提出了一种扰动补偿自适应控制器。该控制器将系统的相位滞后特性看作内部扰动,将其和系统的外扰一同作为系统总扰动加以补偿,既不需要被控对象和扰动的精确数学模型,也不需要反复手动调节参数,通过自适应算法即可使系统输出信号与参考信号保持一致。
1 控制器设计
1.1 基于LMS滤波器的自适应控制
自适应滤波器由系数可调的数字滤波器和自适应控制算法2部分组成,通过某种自适应算法对滤波器系数进行调整,以获得期望响应。本文选用的自适应算法为最小均方(least mean square,LMS)算法。该算法的系数迭代更新公式[7]为
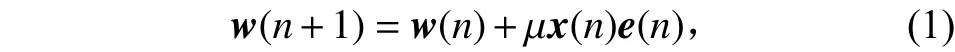
其中:w(n)为权系数,w(n)=[w1(n),w2(n)]T;µ为收敛系数;x(n)为参考信号,x(n)=[x1(n),x2(n)]T=[cos(2πf0n),sin(2πf0n)]T;e(n)为误差信号。
相应地,应用该算法进行权系数更新的线性自适应滤波器称为LMS自适应滤波器(LMS滤波器)。图1所示为利用LMS滤波器在单输入单输出(SISO)系统中进行定频正弦振动激励的控制框图。

图1 基于LMS滤波器的自适应控制Fig.1 Adaptive control based on LMS filter
图1中,u(n)和y(n)分别为对象的输入和输出信号,u(n)=wT(n)x(n);振动激励系统期望产生的振动信号为任一正弦信号

其中:D为振幅;f0为频率;γ为初始相角。
假设控制对象在频率f0处的幅频特性值为A、相频特性值为φ,若误差信号e(n)=d(n)-y(n)=0,则输出信号y(n)=d(n)=Dsin(2πf0n+γ),那么控制信号u(n)应该满足:
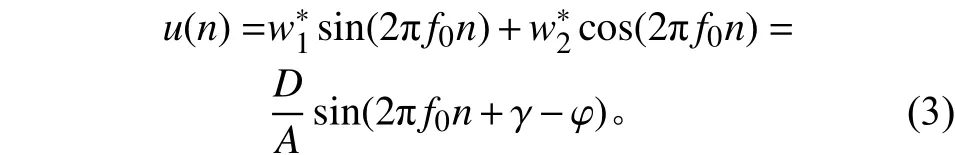

然而,实际控制对象的幅频和相频特性难以精确获知,无法通过式(4)直接求得,故由式(1)迭代求解,将它们分别与相应参考信号相乘并相加后输入系统,便可获得期望的输出信号。
但该算法的缺点是对控制对象的相频特性要求很高,式(1)迭代收敛的条件为考虑到µ>0,A>0,相频特性φ的绝对值应为(0,90°),且当φ的绝对值越接近90°,µ的收敛域越小,因而控制频带宽度受限;并且从式(3)可以看出,参考信号频率单一,无法应对由系统非线性特性产生的谐波失真以及系统外部干扰等造成的复杂情况。因此,需要从改变对象本身频率特性出发,辅以补偿系统扰动,引入线性自抗扰技术。
1.2 线性自抗扰技术
文献[8]以线性化形式设计自抗扰控制器,提出线性自抗扰控制(linear active disturbance rejection control,LADRC)。对于SISO系统,典型二阶线性自抗扰控制器结构如图2所示。

图2 二阶线性自抗扰控制器结构Fig.2 Two-order linear active disturbance rejection control
二阶线性自抗扰控制器各参数为

其中:z1、z2和z3分别为输出的观测项、输出变化的观测项和观测扰动项;β1、β2和β3为各状态观测器系数;b为补偿因子;kp、kd分别为PD调节器的比例系数和微分系数。
线性自抗扰技术本身也可应用于正弦振动控制中,但其在某个频点为获得高精度而设定好的参数应用于其他频点时往往效果不理想,需要重新调节参数;而本文提出的控制算法将其与自适应算法结合,无须调节参数即可在宽频带实现高精度的正弦信号追踪,具体对比见本文第2章。
1.3 扰动补偿自适应控制算法
本文针对基于LMS滤波器的自适应控制的收敛要求,从改变对象本身频率特性的角度出发,提出扰动补偿自适应控制算法(active disturbance rejection with adaptive control,ADRAC)来实现更宽频带的SISO系统的高精度输出,算法结构如图3所示。算法包括线性自抗扰和自适应控制2个部分:线性自抗扰作为内环,将被控对象相位滞后特性看作对象内部扰动,通过主动观测补偿,改善对象的相频特性,进而提高自适应控制时对象的可控频带宽度,以实现期望的频带宽度;除此以外,状态观测器(LESO)的引入还能有效观测系统外部扰动并进行补偿,增强系统抗外界扰动的能力,从而提高自适应控制应对复杂情况的能力,提高控制的精度。基于LMS滤波器的自适应控制作为外环控制,其输出并不直接作用于对象,而是作用到调节相频特性后的系统上,最终实现对期望信号的跟踪控制。

图3 扰动补偿自适应控制Fig.3 Active disturbance rejection with adaptive control
下面以具体对象为例,详细说明新设计的扰动补偿自适应控制器如何实现改变对象频率特性以拓宽自适应可控频带,及其在抗扰能力上的优势。
1.3.1 拓宽可控频带
以传递函数

所示的二阶系统为对象,其幅频和相频响应曲线(即波特图)如图4实线所示。
由图4可知,该对象在3 Hz左右相位滞后便大于90°,因此自适应稳定频率上限小于3 Hz,不满足实际需求。通过调整扰动补偿参数[b,ω0,kp,kd],可以实现对对象频率特性的调节,其中补偿因子b反 映了对象系统的固有特性,是决定补偿强弱的因子。对理想二阶系统,b是系统传递函数分子上的常系数[9],因此这里的b=400。文献[10]给出了用带宽概念确定观测器系数的简便方法:观测器的特征多项式为
为了更好地估计对象的状态和总扰动,观测器系数的选取应当使得特征多项式稳定,而稳定且有较好过渡特性的特征多项式形式[10]为
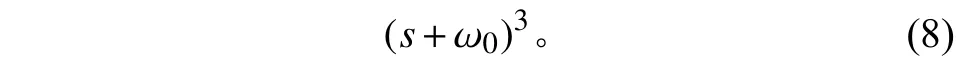
因此,为获得稳定的状态观测器,观测器系数应选取为
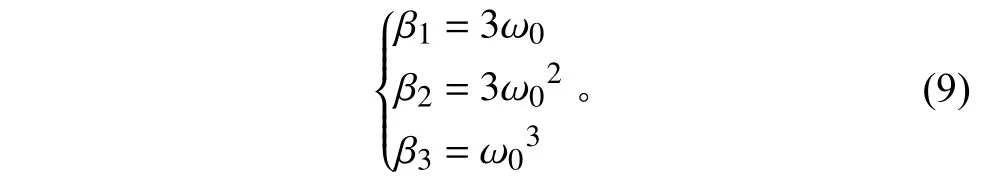
通过选取不同的ω0可以使得观测器的频率特性发生改变。一般情况下ω0的适应范围很广,这里主要针对对象相频特性的调节结果来选取。
根据图4所示的系统相频特性,调节扰动补偿参数,使得系统相频曲线在(-90°,90°)区间的频带满足实际需求,且尽量远离边界,以满足自适应控制收敛的必要条件。最终参数设置为[b,ω0,kp,kd]=[400,100,20,0.2]。调整后系统的幅频特性曲线如图4虚线所示,系统相位滞后达到90°的频点约在40 Hz,远大于之前的3 Hz,实现了针对该对象拓宽自适应可控频带范围的目的。
扰动补偿参数[b,ω0,kp,kd]的取值不是唯一的,例如对于补偿因子b, 假设b的 理想值为b∗,实际运用中当b∈[0.1b∗,10b∗]或更大的范围都能满足稳定[9]。图5是在参数成倍变化时对象的波特图,可见针对系统的相频要求,扰动补偿参数有很宽的适应范围。这说明按相频特性要求寻找到合适的扰动补偿参数并不困难,且这种对参数的不敏感体现了算法的鲁棒性。
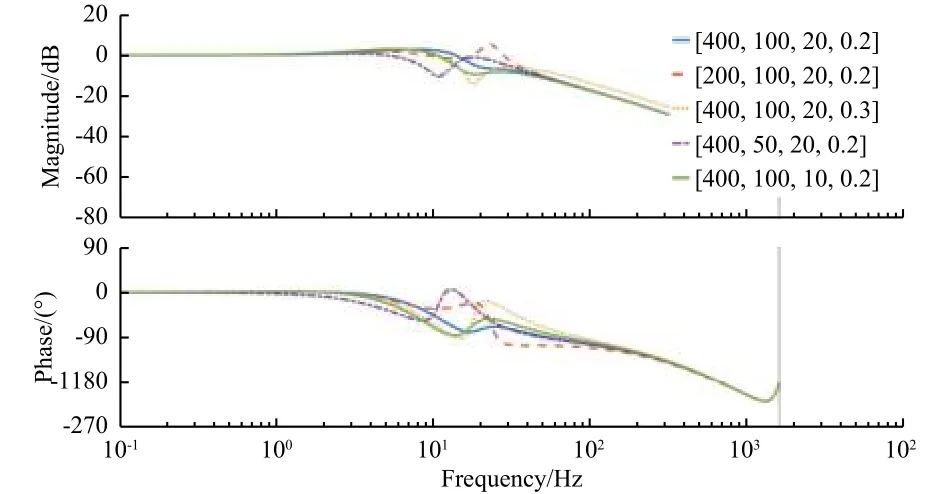
图5 不同参数设置下系统波特图Fig.5 Bode plots for different parameters
1.3.2 抗扰性
仍以传递函数式(6)为仿真对象,仿真程序通过MatLab/SimuLink软件编写。线性自抗扰控制中同名参数设置均与1.3.1节的扰动补偿参数设置一致,自适应收敛系数设置为0.001,采样频率3200 Hz。期望信号为幅值为1 mm的1 Hz正弦信号。
1)对象无干扰,即扰动D(t)=0,稳定后3种控制仿真结果的误差如图6所示。可以看到,自适应与扰动补偿自适应中由于控制器中具有“自我求解”能力的自适应算法的存在,误差基本为0;而同扰动补偿参数的线性自抗扰控制器还存在着幅值约为0.02 mm的误差。
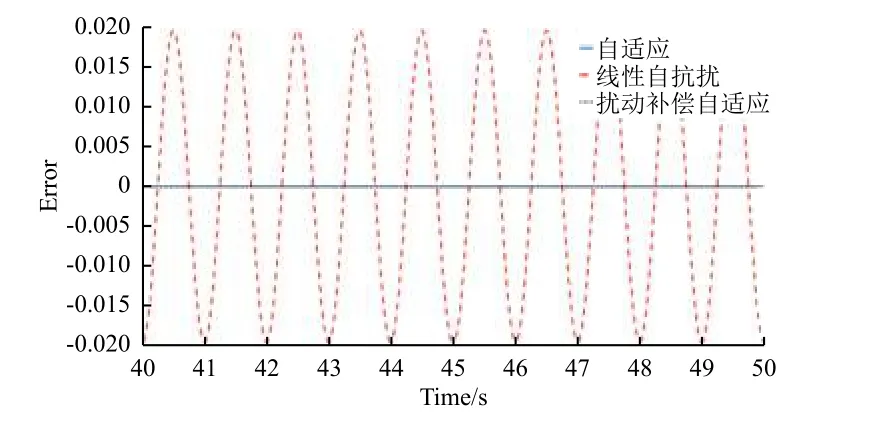
图6 3种控制仿真的误差对比(无干扰)Fig.6 Errors in three different simulations
2)对象有干扰
然而实际微激励系统受到外界干扰,如摩擦等影响,输出中存在着谐波(参见图7),同时系统的不完全卸载造成位移上存在一定量的偏置。

图7 实际微激励系统1 Hz、z向0.4 mm平动自适应控制位移响应(频域)Fig.7 Actual displacement error of adaptive control in frequency domain
从图7分析可知,外界干扰可以表示为
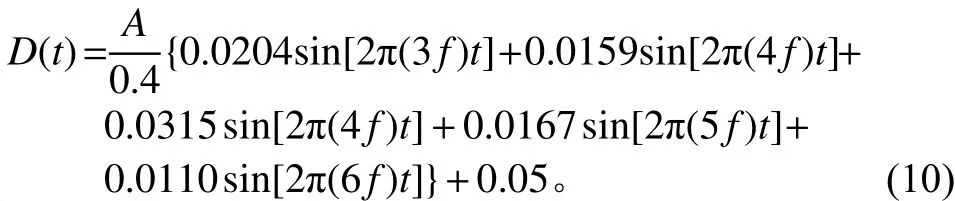
其中:A为期望正弦信号幅值;f为期望正弦信号频率。
在对象输出端加入如式(10)的扰动,稳定后3种控制仿真结果的误差如图8所示。可以看到,基于LMS的线性自适应控制器对控制对象输入信号单一,对于扰动无补偿能力,误差峰-峰值高达0.18并且存在着0.05的偏置;线性自抗扰控制与扰动补偿自适应控制中存在对扰动具有观测能力的线性状态观测器(LESO)以及相应补偿措施,其误差结果无常量偏置,线性自抗扰的误差峰-峰值略大于0.03,扰动补偿自适应的误差峰-峰值略小于0.03。

图8 3种控制仿真的误差对比(有干扰)Fig.8 Errors in three different simulations
综合1.3.1节中对于扰动补偿自适应控制器中算法对控制对象频率特性调节能力的说明,扰动补偿自适应算法在有效改变控制对象频率特性的同时,还能够实现对输出端扰动的观测和补偿,提高控制精度。
2 Hexapod微激励系统振动控制联合仿真
Hexapod多自由度微激励系统属于多输入多输出(MIMO)系统。图9为Hexapod平台多自由度微激励系统及针对其于Adams软件中搭建的相应仿真模型。
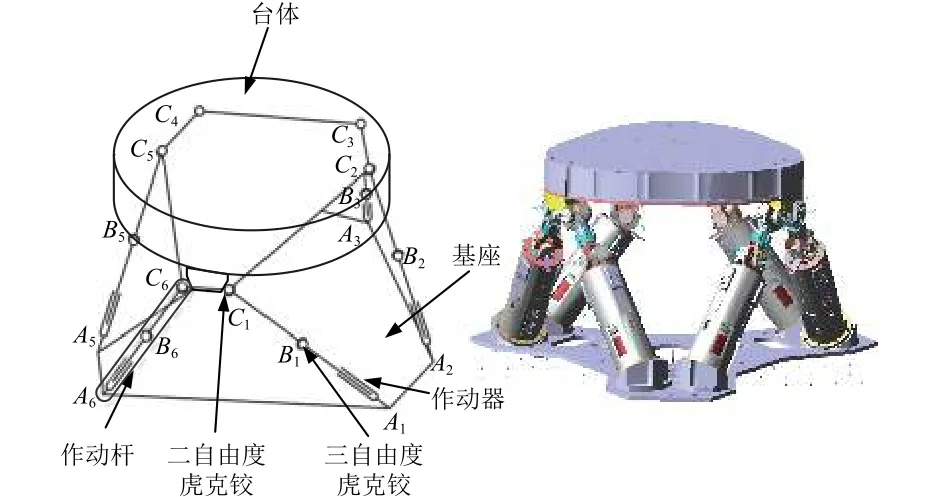
图9 Hexapod平台多自由度微激励系统及其仿真模型Fig.9 Diagram and Adams model of Hexapod platform
微激励系统在低频段时,加速度传感器的响应很小,控制中主要采用位移反馈,其控制框图如图10所示:以上平台各自由度的位移为期望信号,通过运动学反解得到各作动杆的位移期望信号,从而将多输入多输出控制问题转化为多个单输入单输出控制问题;各杆位移期望信号与该杆实际位移的误差输入扰动补偿自适应,同时实际位移信号作为扰动补偿自适应中状态观测器的输入,并将与所期望产生的振动同频率的单位正弦和余弦信号作为扰动补偿自适应的参考信号输入,即可得到各作动杆的控制输入。
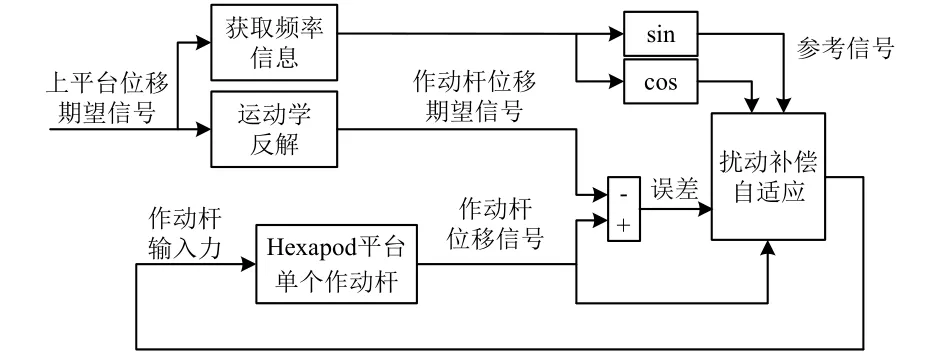
图10 扰动补偿自适应低频控制框图Fig.10 Low-frequency control using ADRAC
仿真设定:激励系统台体沿z向平动,期望信号为幅值0.4 mm正弦信号,前10 s为0.5 Hz定频仿真,10 s后扫频仿真,扫频频率0.5~20 Hz、速率0.5 Hz/s,自适应收敛系数0.005,线性自抗扰参数及扰动补偿自适应中扰动补偿参数设置均为[b,ω0,kp,kd]=[400,100,2.5,0.1]。联合仿真结果如图11和图12所示。
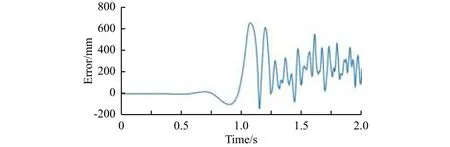
图11 自适应仿真z向位移响应误差Fig.11 z-direction displacement error in adaptive control simulation
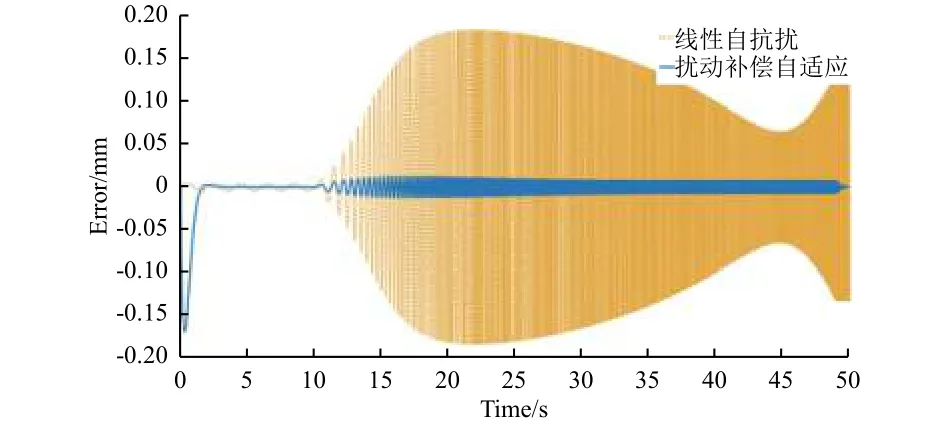
图12 线性自抗扰和扰动补偿自适应仿真z向位移响应误差Fig.12 z-direction displacement error in LADRC and ADRAC simulation
由图11可以看到,自适应控制很快发散,台体z向运动量远超模型设计值,模型解构。这表明基于LMS滤波器的自适应控制应用于Hexapod多自由度微激励系统低频控制可控频带非常窄,上限小于0.5 Hz。
由图12可见,扰动补偿自适应扫频时由于自适应算法迭代需要一定的时间,所以误差(峰值0.008 mm)相对于定频时大一些;在49 s扫频结束后,算法很快恢复定频时的更高精度(误差峰值0.001 mm)。图13显示,对于仿真模型的力输入符合运动学规律,证明仿真无误。
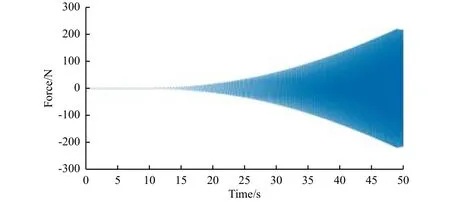
图13 扰动补偿自适应仿真中的模型输入量Fig.13 Input in ADRAC simulation
图11 与图12实线对象的差异,验证了扰动补偿自适应应用于Hexapod多自由度微激励系统以拓宽控制频带的有效性。图12虚线对象验证了在1.2节所提的线性自抗扰对于正弦振动控制,在不调节扰动补偿参数的情况下,难以在宽频带实现高精度的正弦信号追踪的缺陷;其与图12实线对象的对比,验证了扰动补偿自适应无须反复调节参数的优越性。
联合仿真的结果证明了扰动补偿自适应控制算法用于Hexapod多自由度微激励系统的可行性与高效性。对比3种控制算法的联合仿真结果,扰动补偿自适应控制算法在改变控制对象频率特性、拓宽自适应控制频带的同时,实现了对Hexapod多自由度微激励系统的高精度控制。
3 实验验证
实验于如图14所示的Hexapod平台多自由度微激励系统上进行。

图14 Hexapod平台多自由度微激励系统实物Fig.14 Picture of the Hexapod platform
自适应算法因稳定条件中对被控对象相位延迟的要求而限制了其在工程上的应用,经典的超前校正环节[11]与扰动补偿自适应中的线性自抗扰环节一样具有调节被控对象频率特性的作用,可以尽量减小校正环节与被控对象构成的广义控制对象的相位延迟,从而使得基于LMS滤波器的自适应控制能够应用于Hexapod多自由度微激励系统低频控制中。图15为引入超前校正的自适应控制框图。

图15 引入超前校正的自适应低频控制框图Fig.15 Low-frequency control diagram using adaptive control with lead correction
利用已有的Hexapod多自由度微激励系统,应用上文所述的扰动补偿自适应及引入超前校正环节的自适应搭建实时控制系统进行实验,验证控制策略的有效性。实验中自适应收敛系数为0.005,扰动补偿参数设置为[b,ω0,kp,kd]=[400,100,8,0.5]。台体沿z向平动,期望信号为幅值0.4 mm的1 Hz正弦信号。扰动补偿自适应控制的实验结果见图16。可以看出,仿真中所添加的干扰近似地模拟了实际工况中的干扰,实验在控制上取得了与仿真相近的结果,为探究Hexapod多自由度微激励系统干扰模型的建立提供了一定经验。
扰动补偿自适应控制与引入超前校正环节的自适应控制的对比(图17)证明,两者均能有效调节被控对象频率特性,使得自适应控制得以应用于Hexapod多自由度微激励系统低频控制中;但前者在调节被控对象频率特性的同时,可以有效补偿系统所受外部扰动,获得更高的控制精度,误差峰-峰值仅为0.035 mm,而后者的自适应控制的误差峰-峰值为0.15 mm;并且前者消除了常量偏置。同时,由图18可以看到,扰动补偿自适应控制取得所需的工作频带(实验做到25 Hz),未发散。
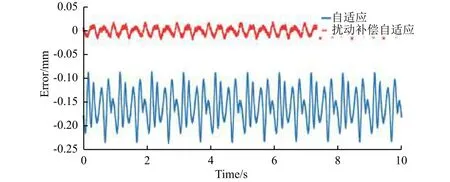
图17 引入超前校正的自适应和扰动补偿自适应z向位移响应误差对比Fig.17 z-direction displacement error in experiments of adaptive control with lead correction and ADRAC
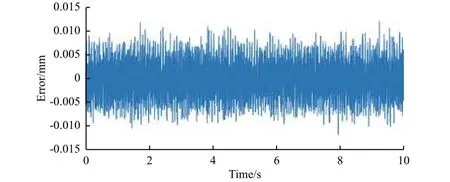
图18 扰动补偿自适应25 Hz定频z向位移响应误差Fig.18 z-direnction displacement error in the ADRAC experiment
4 结束语
本文以二阶系统为对象,详细介绍了扰动补偿自适应控制如何针对对象相频特性,调节算法中的扰动补偿参数,拓宽自适应可控频带,以获得期望的控制频带。通过有无干扰的仿真对比,体现了扰动补偿自适应算法相比于改进前的自适应算法在抗扰性上的优势。
以Hexapod多自由度微激励系统为对象的仿真和实验结果表明,扰动补偿自适应控制算法相比于单独使用线性自抗扰算法,以及引入超前校正环节的自适应算法,在低频控制时能够更有效地实现所需频带高精度正弦微振动信号复现,显示出该控制算法的实际工程应用价值。

