瑞雷波多模式频散曲线的能量计算研究

许崇彩 王国富 闫伟

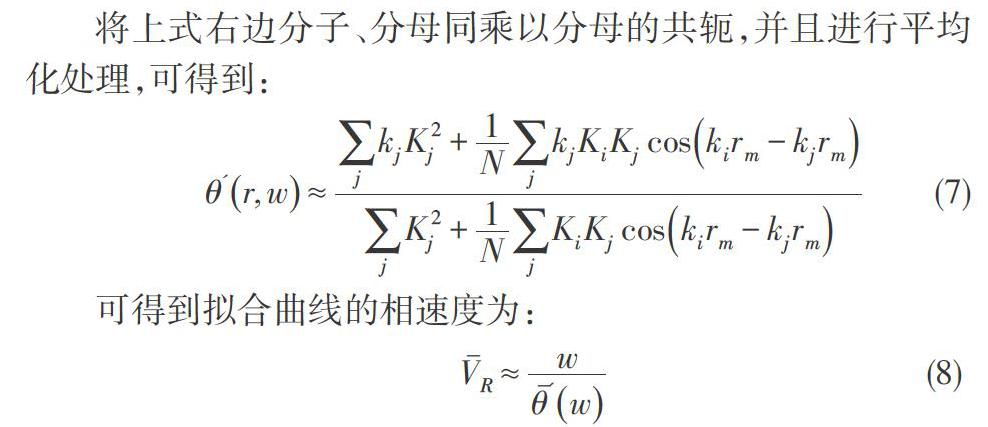
摘要：瑞雷波勘探技术具有快速、无损、衰减小、抗干扰能力强等优点，广泛应用于实际的工程勘探。在实际的工程勘探中提取的瑞雷波频散曲线只有一条，是正演中多个模式频散曲线的拟合，但是在正演中无法直接拟合成一条曲线。因此通过计算研究瑞雷波的能量分布，能够直接计算出各个模式频散曲线的能量相对值。通过与有限差分模拟法对比，实验表明：该算法能够实现不同模式频散曲线的能量相对值的计算，为频散曲线拟合提供了直接的数据基础。

关键词：瑞雷波；频散曲线；能量；数据

中图分类号：TP631 文献标识码：A 文章编号：1009-3044（2018）26-0236-04

Abstract： Rayleigh wave exploration technology has the advantages of fast， lossless， low attenuation， strong anti-interference ability， and is widely used in practical engineering exploration. There is only one dispersion curve of Rayleigh wave in the actual engineering exploration， which is the fitting of the multiple modes dispersion curve in the forward process. But it can not be directly fitted into a curve in forward modeling. Therefore， by studying the calculation of Rayleigh waves energy distribution， we can directly calculate the energys relative value of each mode dispersion curve. Compared with the finite difference method， the experimental results show that the algorithm can calculate the different modes relative value of dispersion curve ， which provides a direct data foundation for the dispersion curve fitting.

Key words： rayleigh wave； dspersion curve； energy； data

瑞雷波勘探技术有快速、无损、衰减小、等优点[1-4]近年来被广泛应用于工程勘探等方面[5-6]。Xu等人的有限差分法的正演算法能够模拟不同地层的瑞雷波频散曲线[7-8]。瑞雷波的能量研究全部集中在有限差分法的模拟和多模式瑞雷波的直接叠加[9-10]。本文结合实际勘探将针对不同的地层，对多模式瑞雷波的能量进行相对值计算，为实际的工程勘探提供直接的理论依据。

1 能量相对计算原理

瑞雷波法应用在实际的工程勘探中的震源是地表竖向激振型震源，且作用力的范围是在半径为[r0]的半圆内。

它的实质是瑞雷波的各个模式相对幅值平方（各个模式的相对能量）为权值对波数进行加权叠加。因此计算各个模式的相对位移，就能够得知各个模式所占的能量大小，就能解释实际应用中频散曲线的分布，并且为“之”字形的出现提供理论依据。

2 实际勘探能量应用

本项目野外勘探区为陕西省府谷县西北部的三道沟井田。该区属于典型的黄土丘陵沟壑地貌，全区地形支离破碎，沟壑纵横，区内植被稀少，梁顶、谷坡、沙丘屡见不鲜。区内地势中西部高、四周低，地面陡峭。该区浅层部分广泛分布第四系浅黄色粘土、亚粘土、细砂层。

2.1 第一测点

通过鉆井探勘，测得第一个测点的频散图和视横波速度[+∞]。结合勘探资料和第一测点的视横波速度分布，经过反复的调试，最后得到该地层的分布如表1所示。

诺波夫算法得到的正演频散曲线和横波分布图和实际提取的曲线如下所示。

第一测点的能量相对分布如表2：由相对幅值分布表可以看出，在3Hz之间，只有基阶模式，3-7Hz出现高阶模式，基阶依旧占据主要能量，在7.5-10Hz，基阶模式的能量降低，高阶占据主要能量。由半波长可知高阶模式在第一层地质内出现。高阶模式出现后，相应的拟合因子[θ'w]变大，由曲线拟合计算可知，高模模式阶段的相速度会相应的减小，但是减小的幅度很小。

模式识别反演算法对该实际频散曲线进行反演，除了横波速度，初始模型的其他参数使用该地层中的参数，反演出的横波速度值为[1360，2052，2704]，反演频散曲线、正演基阶频散和实际频散拟合如图3所示。

结合钻井探测可知该测点的地层分为三层，分别为：粘土层、煤层、岩石层。结合反演数据，反演频散曲线能够符合实测曲线。从该图可以看出反演的频散曲线不仅能够和实际的频散曲线拟合，而且和正演模型计算的频散曲线几乎完全重合，其中得到的横波速度差值矩阵为[-9，30，4]。这说明，利用能量计算能够直接的判断实际采集频散曲线阶数，在测点中，基阶占主要能量，因此测点的频散曲线能够和基阶拟合。但在频率为0-0.2Hz之间曲线相差比较大，是由于实际频散曲线提取中，频率无法达到超低频，导致误差较大，但在合理范围内。实际钻井探测结果相吻合。

2.2 第二测点

第二个测点的频散图和视横波速度[+∞]。结合勘探资料和第二测点的视横波速度分布，经过反复的调试，最后得到该地层的分布如下所示：

诺波夫算法得到正演的频散曲线和横波分布图和实际提取的曲线如下所示：

第二测点的能量相对分布如表4所示：由该表格可以看出：0-4Hz，只有基阶模式，4.5-6Hz出现高阶模式，但基阶依旧占据主要能量，在6.5-10Hz，各模式交替占主要能量；由半波长可知，高阶模式在第一层地质内出现。高阶模式出现后，相应的拟合因子[θ'w]变大，由曲线拟合计算公式[VR≈w/θ'w]可知，高频段的相速度会相应的减小，因此该地层产生的频散曲线的拟合曲线能够与实际频散能够拟合。

与第一测点的反演过程一样，反演出的横波速度值为[1302，2719，2064]，反演频散曲线、正演基阶频散和实际频散拟合如下所示：

结合钻井探测可知该测点的地层分为三层，分别为：粘土层、岩石层、煤层。从该图可以看出反演的频散曲线不仅能够和实际的频散曲线拟合，而且和正演频散曲线相差不大，得到的横波速度差值矩阵为[-51，-19，18]。该测点的频散曲线在6Hz之前，基阶为主，6Hz之后是多模式交替，因此该测点的频散曲线和理论频散曲线有轻微差别，但是能够拟合。但是在频0.2-0.5Hz、1-1.3Hz之间的频散曲线相差比较大，由半波长原理可得其对应深度为600m-1800m、290m-337m，说明在该区域存在岩体破裂、缝隙、陷落柱等情况，与实际钻井探测深度相差约为10m。其中与煤层相接处存在岩体破裂、缝隙、陷落柱等情况。

3 结束语

在研究瑞雷波在多层的传递的函数计算基础上，采用理论计算与现场实际测试相结合的方式进行验证分析，得出以下结论：递增地层中，多模式瑞雷波能量分布在低频段以基阶为主，高频阶段，多模式并存；非递增地层中，能量分布表现多模式混合，频散曲线可能出现回折；实际提取的频散曲线中，通过能量计算分布可以对实际频散曲线进行合理预测。

参考文献：

[1] Socco L V， Foti S， Boiero D. Surface-wave analysis for building near-surface velocity models—Established approaches and new perspectives[J]. Geophysics， 2010， 75（5）：75A83-75A102.

[2] Zhang S， Li X， Jeong H， et al. Modeling nonlinear Rayleigh wave fields generated by angle beam wedge transducers—A theoretical study[J]. Wave Motion， 2016， 67： 141-159.

[3] Bao X， Dalton C A， Ritsema J. Effects of elastic focusing on global models of Rayleigh wave attenuation[J]. Geophysical Journal International， 2016， 207（2）：1062-1079.

[4] Ma S， Audet P. Seismic velocity model of the crust in the northern Canadian Cordillera from Rayleigh wave dispersion data[J]. Canadian Journal of Earth Sciences， 2017， 54（2）：163-172.

[5] Maranò S， Hobiger M， F?h D. Retrieval of Rayleigh wave ellipticity from ambient vibration recordings[J]. Geophysical Journal International， 2017， 209（1）：334-352.

[6] Palomeras I， Villase?or A， Thurner S， et al. Lithospheric structure of Iberia and Morocco using finite-frequency Rayleigh wave tomography from earthquakes and seismic ambient noise[J]. Geochemistry， Geophysics， Geosystems， 2017， 18（5）：1824-1840.

[7] Beilina L. Domain decomposition finite element/finite difference method for the conductivity reconstruction in a hyperbolic equation[J].Communications in Nonlinear Science and Numerical Simulation， 2016， 37： 222-237.

[8] Xu Y， Xia J， Miller R D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach[J].Geophysics，2007，72（5）：SM147-SM153.

[9] 辛维， 闫子超， 梁文全， 等. 用于弹性波方程数值模拟的有限差分系數确定方法[J]. 地球物理学报， 2015， 58（7）：2486-2495.

[10] Pal J， Ghorai A P. Comparison and Analysis of Surface Waves Propagation in Initially Stressed Dry Sandy Layer Using Conventional and Time Dependent Finite Difference Scheme[J]. International Journal of Applied Engineering Research， 2016， 11（10）：7119-7124.

[11] 刘建宙. 有限差分法在瑞雷波波场正演模拟中的应用[D]. 中国地质大学 （北京）， 2014.

[通联编辑：代影]