基于灰色补偿BP神经网络优化组合模型的车辆装备冷却系腐蚀预测

徐安桃，李锡栋，周慧，乔渊博，吴正日

（陆军军事交通学院 a. 投送装备保障系；b. 学员5大队研究生队，天津 300161）

车辆装备发动机冷却系长期服役于常温与高温 交替环境下，金属零部件工作环境复杂、恶劣，极易发生化学或电化学腐蚀，破坏冷却系，从而影响车辆装备保持良好的性能状态，缩短装备的使用寿命[1-2]。因此，为维持车辆装备的良好性能，延长车辆装备的服役年限，对冷却系腐蚀进行准确预测就显得尤为重要了。

冷却系金属材料的腐蚀是一个极为复杂的物理化学过程，受到诸多因素影响，如冷却液、缓蚀剂类型、酸碱度、工作温度等。这些腐蚀、抗腐蚀因子相互影响，共同作用构成了一个复杂恶劣的冷却系环境[3-5]。由于这些因子之间的关系具有很大的不确定性与模糊性，可视之为随时间而变化的灰色量，则冷却系金属的腐蚀就可视为一个信息不完全、不确定的灰色系统。因而，可采用灰色系统理论对其腐蚀问题进行研究。GM(1,1)模型作为一种最为常用的灰色预测模型，能克服“贫信息、少数据”等问题，使不确定的灰色量化，现已广泛运用于工业控制领域[6-7]。但该模型仍存在一些问题：1）GM(1,1)模型适用范围受限，仅限于完全等时距序列；2）传统 GM(1,1)模型建立后，灰色参数是固定不变的，忽略了灰色系统随时间推移所发生的变化，因而不适用中长期预测；3）不具有自学习、自组织及自适应性能力，处理非线性信息能力偏弱。神经网络模型具有强大的非线性处理能力、自组织适应性能力及学习能力等特点，可与灰色预测模型形成优势互补，建立起一个性能更优的灰色神经网络组合模型[8-9]。

针对传统 GM(1,1)模型的缺陷，文中拟在传统GM(1,1)模型基础上，结合新陈代谢思想，建立一种新陈代谢加权不等时距模型MUGM(1,1,λ)。此外，引入遗传算法优化BP神经网络模型对MUGM(1,1,λ)模型进行残差修正，进一步提高模型精度，以实现对车辆冷却系腐蚀的精准预测。

1 模型基本理论

1.1 MUGM（1,1,λ）模型

设 不 等 时 序 原 始 数 列 为 { x(0)(ti)} ={ x(0)(t1),x(0)(t ),… ,x(0)(t )}，以时距作为乘子，对其进行一次

2

n累 加 生 成 1-AGO序 列 { x(1)(ti)}， 有 x（1）(ti)=。以1-AGO序列 { x(1)(ti)}建立UGM(1,1)模型，其白化形式的微分方程为：

式中：参数a为发展系数；u为灰色作用量。将微分方程离散化，可得到：

对于背景值序列 { y(1)(t )}的构建，这里抛弃了

i+1传统的紧邻均值法，引入加权因子λ进行优化，建立相应的加权灰色预测模型（简称UGM(1,1,λ)），即有：

其中λ的值可通过满足实测值与预测值之间的平均相对误差最小来确定的，平均相对误差的计算公式为：

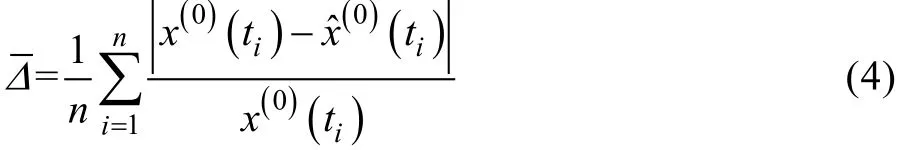
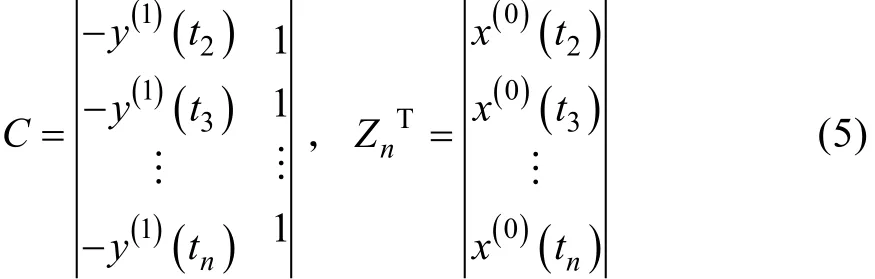
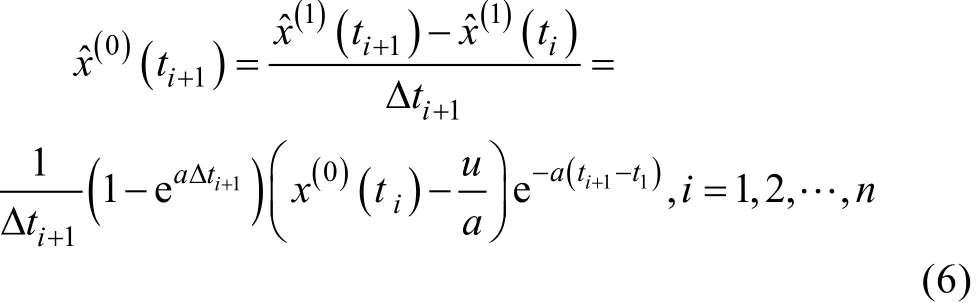
在任何一个灰色系统的发展过程中，时间的推移都会使得旧数据的挖掘开发价值逐渐降低。为更好地反映系统的动态发展，应该及时引入新数据，同时替换老旧数据，实现对建模数据进行更新换代[10]。因而，考虑在上述基础上结合新陈代谢思想对UGM(1,1,λ)模型进行优化，构建新陈代谢加权不等时距 GM(1,1)模型（简称 MUGM(1,1,λ)模型）。具体实现步骤如下[11]：

步骤1，选取原始数据序列作为出初始建模序列，即：

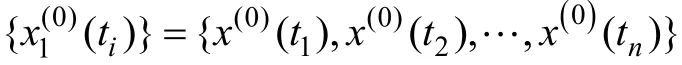
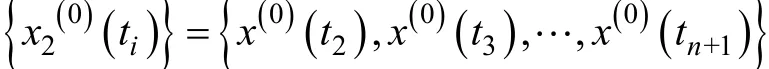
1.2 遗传算法优化BP神经网络

BP算法是一种有监督式的学习算法，它通过反向传播算法可对各个神经元的权值进行不断调整，直到使得输出值与期望值的误差满足要求为止。BP神经网络具有很强的非线性映射能力，理论上可以逼近于任何连续函数。然而，由于该算法本质上是梯度下降法，是一种局部搜索的优化方法，因而存在这样一些问题，如算法的收敛速度慢，且易陷入局部极值点等[12-13]。因此，针对该算法的缺陷，下面引入遗传算法对BP神经网络进行优化。

遗传算法优化BP神经网络算法的流程如图1所示。它共包括三部分：一是BP神经网络的确定，在该部分，首先依据拟合函数输入输出个数来确定网络结构，进而确定遗传算法的长度；二是遗传算法优化，依据遗传算法中种群的选择、交叉及变异等操作确定最优个体，即确定了神经网络各单元的权值；三是BP神经网络的预测，根据经遗传算法优化得到的初始权值、阈值代入神经网络，网络训练后进行预测。

1.3 灰色补偿BP神经网络优化组合模型

1.3.1 算法实现

所谓灰色神经网络组合预测模型，是指将灰色系统理论与人工神经网络通过串联、并联、嵌入、补偿等方式有机结合在一起，取长补短，形成一个二者优势兼具的灰色神经网络组合预测模型[14-16]。文中采用的是基于灰色补偿BP神经网络优化组合模型，其具体流程如图2所示。首先对给定的原始数据序列进行建模，得到MUGM(1,1,λ)模型。运用该模型进行预测，将预测值与原始值进行比较，得到残差序列。然后利用遗传算法优化 BP神经网络模型对此进行适当修正，尔后补偿预测值，得到最终预测结果。

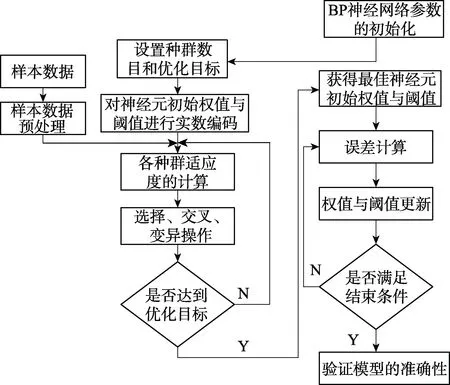
图1 遗传算法优化BP神经网络算法的流程

图2 灰色补偿BP神经网络算法的流程

1.3.2 精度检验

利用小误差概率 P、后验差比值 Q两个参数分级，来判定灰色补偿BP神经网络优化组合模型的精度。参数P、Q的计算公式为：

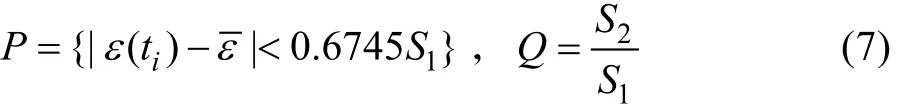
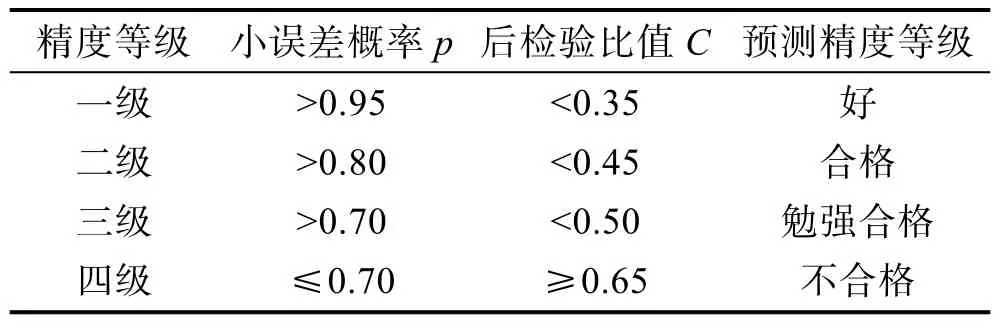
表1 模型精度等级

2 实例分析

选取某型车辆装备冷却系用铸铁在冷却液中测得极化曲线所拟合的自腐蚀电流密度J0，具体见表2。为提高建模的速度与准确，对数据进行负对数处理。对表2中前6组实测数据进行数学建模，对后3组实测数据用于精度检验。按前面所叙述的建模方法，对原始数据进行处理，建立起改进的不等时距灰色动态模型 MUGM(1,1,λ)。

2.1 MUGM(1,1,λ)模型建立

表2 铸铁在冷却液中测得极化曲线拟合的自腐蚀电流密度

模型建立的原始数据序列为:

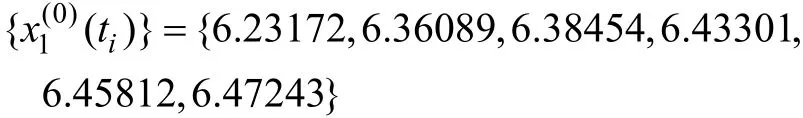
经处理后得到1-AGO序列：

计算得： λ1= 0.757，a1= - 0.00094，u1=6.37577，= 6.56462。添加）并删除），可得到新的原始序列：

计算得：λ2=0.502，a2= - 0.00085，u2=6.39928，）= 6.73446。

继续按步骤操作，可得：λ3=0.481，a3= - 0.00082，

对两个模型进行精度检验，结果见表3。对比两个模型，还可发现MUGM(1,1,λ)模型的平均相对误差较传统 UGM(1,1)低，预测精度更高，特别是对于后3组测试数据的预测，误差明显低于传统UGM模型。这表明通过优化背景值构造与结合新陈代谢思想两种手段，可以有效地提高模型的预测精度。这两种模型的平均误差很小，分别为 2.26%、1.71%。尽管如此，两个模型的后验差比值分别为3.2695、2.4439，小误差概率均为0.1111。对照表1的模型精度表，可判定两种模型精度为四级，预测精度均为不合格。为提高模型精度，以准确反映冷却系金属腐蚀实际，下面采用遗传算法优化BP神经网络对MUGM(1,1,λ)的预测值进行补偿修正。

2.2 神经网络程序实现及结果分析

记残差序列 {e(0)(i)}为 MUGM（1,1,λ）的预测值序列 { xˆ(0)(ti)}与原始序列 {x(0)(ti)}之差，S为预测阶数，则输入样本为 e（0）（i- 1）,e（0）（i- 2 ）,… , e（0）（i- S ），对应输出样本为 e（0）（i）。以Matlab2015b为平台建立遗传算法优化BP神经网络算法，主要的操作步骤为：

1）输入由残差序列 {e(0)(i)}所构成的训练样本（这里预测阶数S取2）。

2）调用函数[inputn,inputps]=mapminmax(input_train)对训练样本数据进行归一化处理。

3）构建神经网络。调用net=newff(inputn,outputn,hiddennum)函数，创建一个2×5×1的BP网络结构。

4）参数初始化。利用遗传算法对网络结构进行初始化，确定最优权值、阈值。

5）训练神经网络。调用函数[net,per2]=train(net,inputn,outputn)对神经网络进行训练。

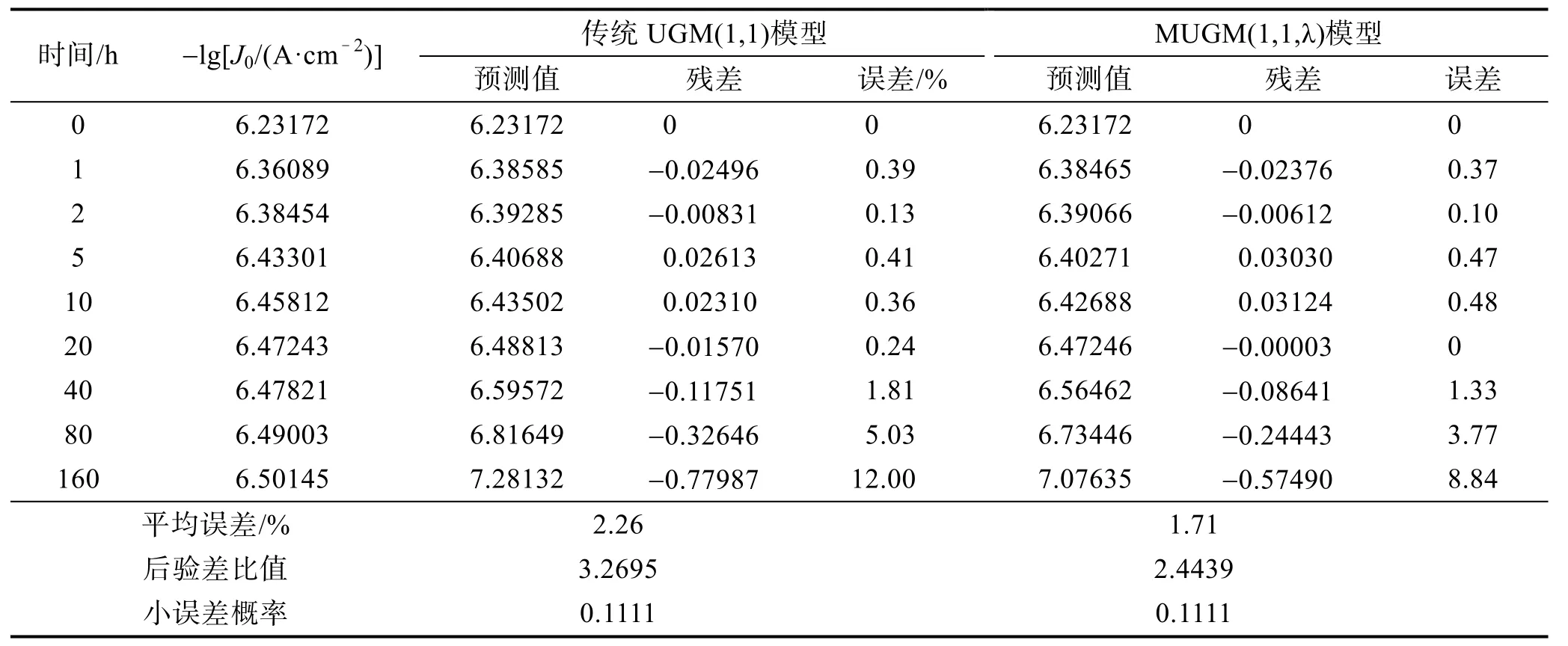
表3 模型预测值及精度检验结果

6）BP网络预测。输入归一化的数据，调用函数an=sim(net,inputn_test)得到预测值。

7）数据还原。调用函数 test_simu=mapminmax('reverse',an,outputps)还原归一化数据，得到最终值。

利用上述的灰色补偿BP神经网络优化组合模型算法程序，预测得到残差序列，并在此基础上对预测值进行补偿修正，即这里只对后3组预测数据进行修正，其结果见表4。

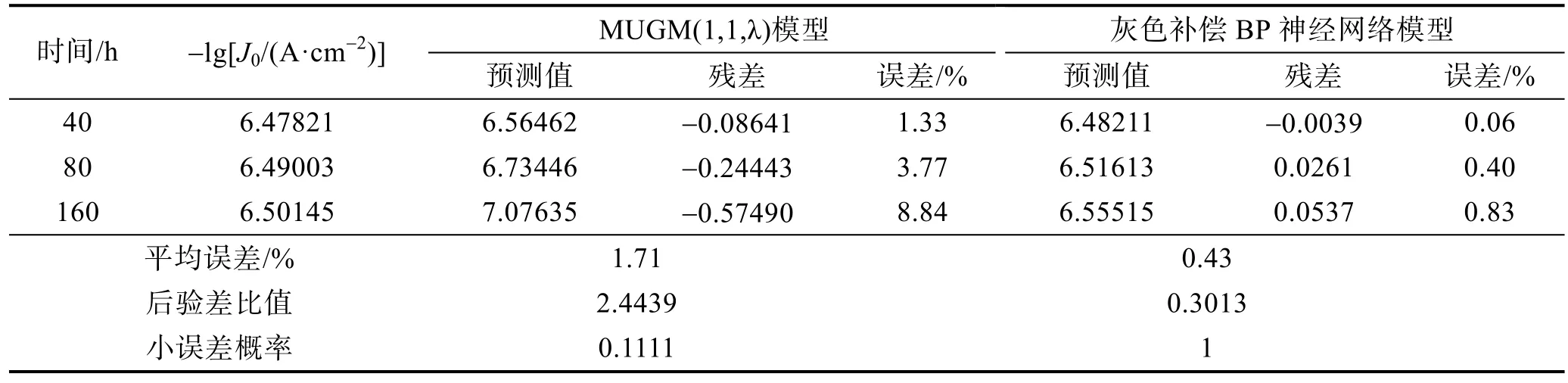
表4 模型预测值及精度检验结果

从表4可以看出，优化组合模型后3组数据的相对平均误差为0.43%，后验差比值为0.3013，小误差概率为1，对照模型精度表，可知该组合模型的精度等级为一级（好）。这表明，利用遗传算法优化 BP神经网络进行残差修正可以大大地提高模型精度。为作更好地比较，现将三种模型的预测结果与误差展示如图3、4所示。

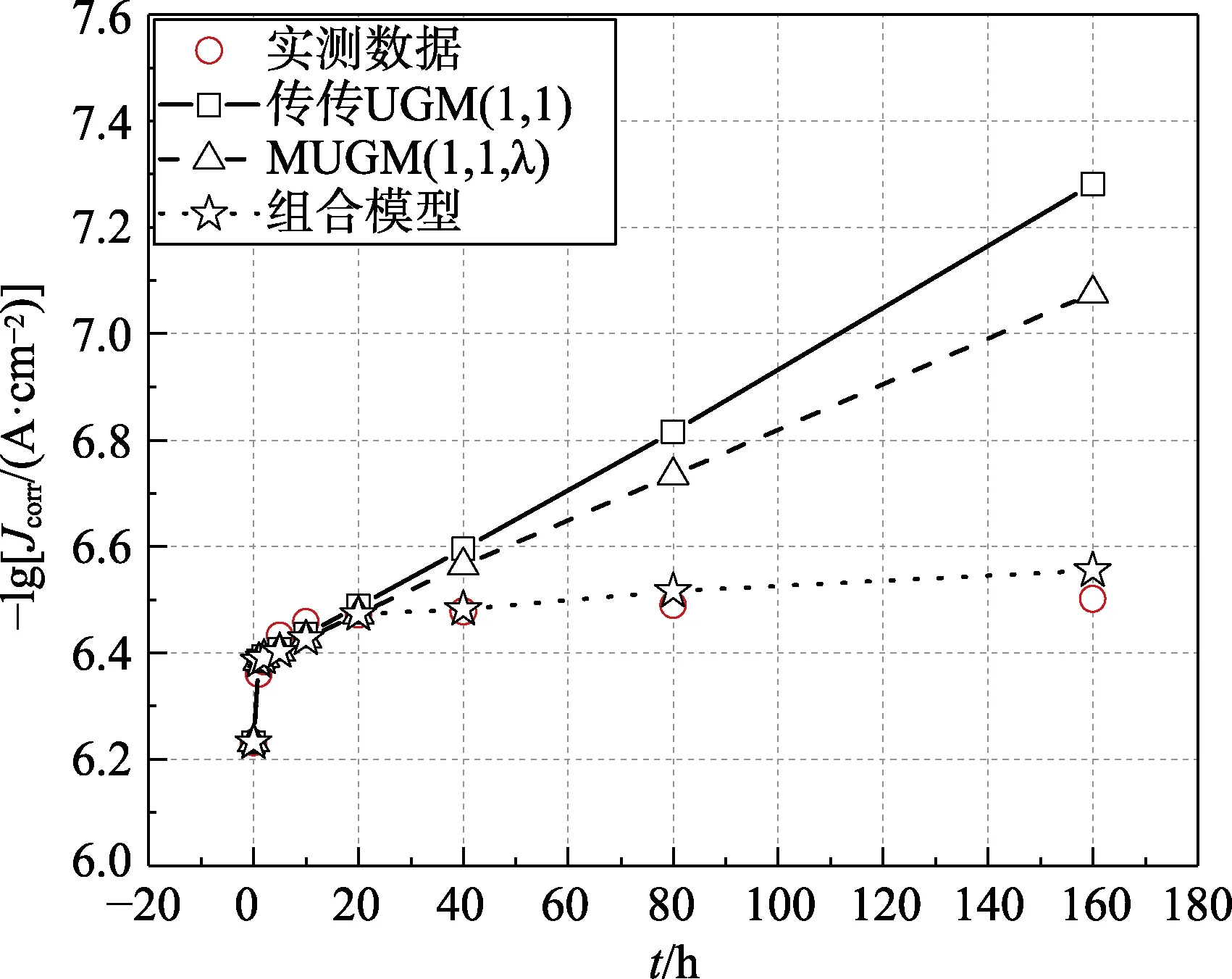
图3 模型预测曲线

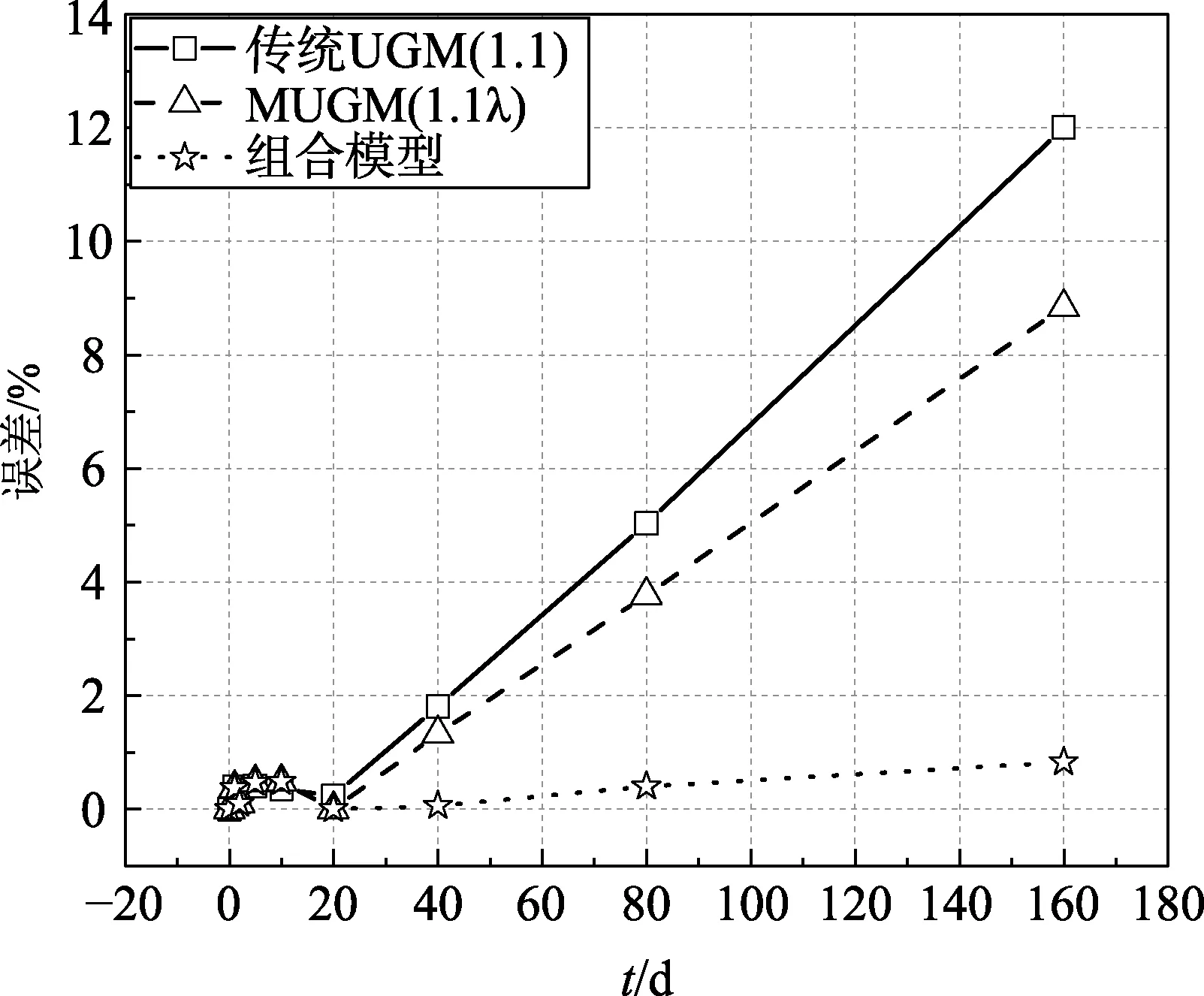
图4 模型相对误差

从图3、4可以看出，传统UGM(1,1)预测值与原始值偏离较大，特别是对于后三组数据的预测误差极大。MUGM(1,1,λ)模型采用了背景值优化与新陈代谢思想两种手段，其精度较 UGM(1,1)有所改善，但是效果也不尽如人意。基于灰色补偿BP神经网络优化组合模型得到的预测值与实测值相差无几，能够较好地反映车辆装备冷却系铸铁材料的腐蚀状态。因此，所建立的灰色补偿BP神经网络优化组合模型能较为准确地实现对车辆装备冷却系金属腐蚀速率的预测，为车辆装备冷却系定期维护保养提供理论支撑。

3 结论

1）车辆装备冷却系金属材料腐蚀原因错综复杂，可被视为一个信息不完全、不确定的灰色系统，因而采用灰色预测模型进行预测具有一定的可行性。

2）对比 UGM(1,1)与 MUGM(1,1,λ)，后者针对UGM(1,1)模型背景值构造的缺陷，以平均相对误差最小的原则引入最佳加权因子加以优化，此外还将新陈代谢思想融入其中。结果表明，MUGM(1,1,λ)较好地改良了传统 UGM(1,1)模型的缺陷，减小了平均误差，但是模型精度均为四级，预测精度不合格。

3）灰色补偿 BP神经网络优化组合模型是在MUGM(1,1,λ)基础上，采用遗传算法优化的 BP神经网络对残差进行修正，以补偿预测值，进而达到提高精度的目的。结果表明，该模型的精度达到一级，能够更准确地预测金属腐蚀速率，为车辆装备冷却系定期维护保养提供理论支撑。