关注素材整合 聚焦核心素养——以《分数的基本性质》为例

（宿迁市湖滨新区晓店中心小学 江苏宿迁 223809）

传统《分数的基本性质》一课，往往落点在规律的探究上，着力点往拄是在探究中发现规律、运用规律，熟练掌握分数的基本性质，为以后分数的约分和通分打好基础。而笔者近日听了一节《分数的基本性质》，有别于传统的教法，立意更高、落点更准、思考更深。教学中紧紧抓住数学知识之间的内在联系，把握学生的认知规律和思维特征，对相关素材进行创造性整合，使教与学的关注点更集中地聚焦在核心素养上。

一、整合原有素材，从熟悉的切入，丰富数感

[片段1]

生：二分之一。（语气轻松，神情愉悦而放松。）

师：能说出一个比它大的分数和一个比它小的分数吗？

师：有没有一个分数与

我们在三年级认识分数之初，无论是认识一个物体的几分之一还是认识多个物体组成的一个整体的几分之一，都是以为切入点认识分数的，可以说就是他们在数学课上真正认识的第一个分数，老师在黑板上写出时，孩子们读数的语气中都透着轻松和亲切。

在本节课的教学中，教者关注到了这一点，对两部分素材进行合理整合，以孩子的知识经验和生活经验同时指向的为切入点进行新知的学习，并在随后的活动中围绕一步步研究，“还是熟悉的配方，却有不一样的味道”，让孩子在逐层推进的活动中不断丰富对的认识，进而丰富对分数的意义、性质以及大小、运算等的感悟。

二、整合操作素材，在具体的活动中，感受几何直观

[片段2]

师质疑：无论是平均分的份数还是涂色表示的份数都不一样，为什么就与相等了呢?

短暂的沉默之后，学生通过画图加以说明：

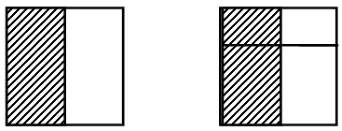
这其实是两个完全一样的正方形，只是一个平均分成2份，一个平均分成4分，第1个涂出了2份当中的1份，第2个涂出了4份当中的2份，因为大正方形是一样大的，所以涂色部分也是一样大的……

在具体的图形操作中认识分数，这是教学中经常用到的方法，而教者加以简单的整合，结合有效的提问，就使孩子们的数学思考更深入，对几何直观的感受更深刻。

三、整合内在联系，在“变”与“不变”中，渗透思辨精神

[片段3]

孩子们在自主探究活动中理解了分数的基本性质之后，思考还在深入：

师：分数的分子和分母同时乘或除以一个不是0的数，分数的大小不变这段话有没有一种很熟悉的感觉？

生：与商不变的规律很相似。

学生通过讨论得出：不能这么说，它们只是大小相等，但意义不同，分数单位也不同……

传统课堂也有沟通分数基本性质与商不变规律之间联系的环节，分数的分子和分母相当于除法中的被除数与除数，分数值就相当于商，所以它们有相同的规律，这是它们“不变”之处，一般也就止于此处。而教者关注的是“不变”背后的“变”，大小不变，但意义变了，这样沟通出的内在联系更完整，这样的思考更深入。

四、整合主问题，在板块式的学习流程中，发展数学思维

[片段4]

师生共同总结进一步理解分数的基本性质。

本课在整体立意和流程设计上开放大气，不纠结于某些知识点的具体教学、某几个数学思想怎样渗透，一改传统线性的序列化的教学流程，以一个主问题贯穿学习过程，在板块式的学习流程中学生自然的主动的学习知识，发展思维。

基于教材的传统教学流程是先用分数表示相同圆中的涂色部分，观察比较它们的大小，找出大小相等的分数，再来从开始研究分子分母的变化规律，在举例观察中归纳出分数的基本性质。这节课则不然，重点研究“与相等的分数”这一主问题，教师只提供举例猜测、自主探究、比较总结、应用规律这一学习线索，具体的探究策略、问题分析解决等孩子需要独立完成，它最大的特点就是开放，开放的学习空间，开放的思维活动，学生的学习自然发生，真正发生。在“与相等的分数”这一大板块学习中，孩子独立思考、分析，利用画图、计算等多种策略解决其中一个问题，再利用空间想象、推理、抽象、模型等思维方式解决一类问题。“与相等的分数”这一小板块的学习，则完全可以通过方法的同化进行自主学习研究，此时不只有知识的生长，更有思维力的提升。