小概率事件原理及其应用

（江西省宜春市奉新县第一中学 江西宜春 330700）

以数据为基础，研究生活中随机事件及其科学规律的一门学科称为概率论，其广泛运用于保险精算，彩票及风险评估等领域.概率论起初研究“赌博问题”，它的创立者费马，惠更斯，帕斯卡，对排列组合方法的应用，成功解决了赌徒的“赌注划分问题”，概率论就此应运而生。

概率是衡量事物发生大小的尺度，一般用数学符号p表示。p属于[0.1]区间之中，一般把概率为1的事件称为必然事件，概率为0的事件称为不可能事件，他们相互对立。

我们将p接近于0的事件称为小概率事件。小概率事件的数学标准为：p＜0.05或p＜0.01。

小概率事件，通俗的讲就是发生的可能性小的事件，虽发生然可能性小，但是不代表不会发生。在概率学中我们定义为：概率很接近于0（即在大量重复试验中出现的频率非常低）的事件称为小概率事件。然而在生活中，小概率事件的发生却不是少有的事情。比如，四川九寨沟县发生7.0级地震，北京地区出现日全食，飞机失事，某人买彩票中了头等奖，等等，都是小概率事件。在某些重要场合，当事件的发生会带来严重后果（飞机失事）时，概率值应选的更小一些比如0.001。当事件的产生后果严重时，小概率事件的阈值更小一些，视情况而定。另一方面，在大量重复独立试验中小概率事件必然会发生，也从数学角度解释了“水滴石穿”，“常在河边走，哪有不湿鞋”。

定理二：（伯努利大数定律）在n次独立重复试验中，记事件A发生的次数是nA，p是A发生的概率，则对于任意ε>0，有由“定律”可知，当独立重复试验一直进行很多次时，事件发生的频率收敛于其概率。独立重复试验次数n足够大，事件发生的频率和概率没有多大的差别，因此发生概率很小的事件在大量重复试验中发生的频率也就很高。

在平常生活中，人们常常用“只要功夫深铁杵磨成针”来形容有志者事竟成。但是也有人认为这是不可能的，如果从概率的角度来说，就会发现很有道理，这是为什么？

这个问题就等价于：假设H“小概率事件一定会发生”

证明过程如下：

设在一次随机事件中事件A发生的概率为ε（ε>0），当ε趋近于无穷小，在n次独立重复试验下，A迟早出现的概率为多少？

解：设A迟早出现为事件B

第一次试验中A不出现的概率为1-ε

p（B）这说明小概率事件迟早会发生的概率为1

假设检验的原理是小概率事件在一次试验中几乎不可能发生，它的基本思想实质上是带有某种概率性质的的反证法。在总体分布未知的情况下，提出关于总体的假设，为了推断总体的未知特性，我们需要根据样本所提供的信息，运用适当的统计量，面对所提出的假设进行判定，假设检验是确定假设正确与否的过程。

例：为了检验某厂生产的产品质量，采取随机抽取的方法，从生产的一批产品中的200件，检查结果发现有5件质量不合格，请问是否符合合格率为99.5%的标准？

解：合格率为99.5%，说明不合格率小于或等于0.5%

在检测的200件产品中，5件不合格产品的概率

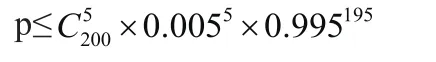
例：在医学界，医疗方法多样，同样一个病症可以用中医也可以用西医治疗，但是疗效却不一样。过去治疗肿瘤，如果采用化学疗法，治愈率是2%，如果采用外科手术法，治愈率是3%，某医生治疗对200名患者采取外科手术进行治疗方法，治愈了6人，那么可以根据治愈率判断治疗方法的效果吗?

解：假设H0∶治愈率P=0.02H1∶治愈率P＞0.02

设X表示治愈患者得数，则X=0.1.2.3….200.由于每个患者的治疗是均等的，随机的，治疗的结果为成功或失败，因此x～B（200.p），当H0成立，p=0.02，λ=np=4 ，可用泊松分布来近似二项分布。

H0成立，治愈人不能过大，设临界值C，给定的显著性水平a=0.05，有p[拒 绝成立]=p[成 立]由泊松分布表可知所以当C=8时，拒绝域（X>8），样本x=6，所以不能拒绝假设，不能断定外科疗法比化学法好。

对小概率事件的研究和分析，可以给我们的统计和决策提供严格的数学依据。分析它，是为了更好的利用它，控制发生条件，让人们更好的认识清楚小概率事件，使其朝着我们期望的方向发展，减少其破坏性。我们应该对其保持正确的态度，怀着贡献福利事业的心去购买彩票，当你购买一份意外保险时，等于买了一份心理保障，拒绝参加街头博彩的骗局。所以说小概率事件的研究无论是生活上，还是工作中都是十分有意义的。