构造问题 分析问题 解决问题——例谈构造法解题的探究

☉山东省肥城市第六高级中学 桑圣一

在解决数学问题的过程中，构造跟原问题有关的数学模型并通过模型的研究而获得解题的方法即为数学构造法，借助某一类我们熟知的问题性质进行未知问题性质的探究是数学构造法的基本原理.

一、几种常见的构造法

1.构造图形法

数学问题的本质往往可以通过数量关系中所隐藏的形的信息得以形象而直观地反映，数与形往往会在图形构造的过程中得以关联到一起并因此将问题表达得更加明朗而清晰.

解法1（一般方法）：根据题意，有

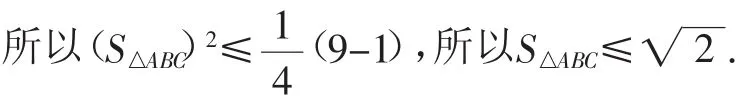
解法2（构造法）：根据题意可知，△ABC的底边是定值，高是变化的，由三角形的面积公式可以推断要求△ABC面积的最大值，只要对点A进行研究即可.如图1，构造平面直角坐标系，令B（-1，0），C（1，0），设A（x，y），则=（-1-x，-y），=（1-x，-y），

即x2+y2=2，

由余弦定理，得4=b2+c2-2，即b2+c2=6，

所以6=b2+c2≥2bc，即bc≤3，

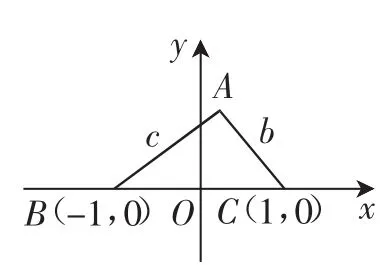
图1

△ABC

根据圆的特点，hmax=r=，所以S△ABC≤.

2.构造函数法

构造函数并利用函数的性质解题的方法即为函数构造法.

例2 对于任意x∈R，不等式2x2-a+3＞0恒成立，求实数a的取值范围.

分析：直接研究不等式左边的条件往往会令学生感觉困难，因此，对不等式进行等价处理才是解题首先应该处理的环节.

令（fu）=2u2-au+1（u≥1），

所以a＜3.

因为f（t）在［1，+∞）上为单调增函数，

所以f（t）≥f（1）=3，即f（t）min=3，所以a＜3.

过程不同的两个方法实质上都是构造函数并在研究函数性质的过程中令问题顺利得解的.

3.构造向量法

包含坐标运算与图形运算的向量知识在高中数学的解题过程中是一个相当重要的工具.因此，很多高中数学问题都会因为向量知识而得到更加快捷的解答.

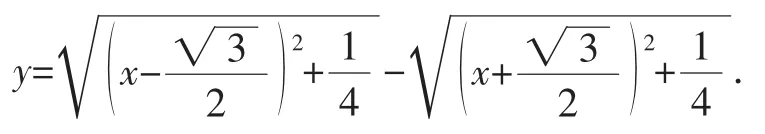
令，m，n两向量不共线，则有|y|=||m|-|n||≤|m-n|=，即|y|≤，所以y∈［-，］.

4.构造方程法

如果能在解题过程中找出已知和未知之间的等式关系，并且观察出其具备方程的某些特性，具体解题时就可以考虑构造方程来解决这一数学问题.

例4 已知a，b，c满足a+b+c=9，ab+bc+ca=24，得

a（9-a-b）+（9-a-b）b+ab=24，整理得a2+（b-9）a+b2-9b+24=0.

将上述方程视为关于a的二次方程，此问题即变成了二次方程有实数解，则有（b-9）2-4（b2-9b+24）≥0，解之，得b∈［1，5］.

5.构造等价命题法

一些直接论证相对困难的数学命题往往可以在构造命题的否命题中来解决.

例5 已知命题“∃x∈［1，2］，使x2+2x+a≥0”为假命题，则a的取值范围如何？

解：根据题意可知，该命题的否定形式“∀x∈［1，2］，使x2+2x+a＜0”是真命题.这与x2+2x+a＜0对x∈［1，2］恒成立是等价的，也就是与a＜-（x2+2x）对x∈［1，2］恒成立是等价的.

设f（x）=-（x2+2x）=-（x+1）2+1，

所以f（x）min=f（1）=-3.所以a＜3.

二、教学感悟

1.培养学生的阅读能力

构造法的顺利构建、实施与学生的创造性思维是紧密相关的，学生必须具备较强的“读题”能力才会对题目本身形成更加独到的领悟与想法.因此，教师在构造法解题教学的过程中首先要重视学生阅读能力的培养，有意识地指导学生进行正确的数学阅读并使其在数学阅读中提升理解能力，把一部分“机械读题”的习惯进行修正并使学生尽快实现“意义读题”，只有这样，学生才能在题目意义的理解中挖掘出解题所需要的隐蔽条件并获得解题的第一步突破.

2.培养学生综合知识的能力

构造法解题不仅对学生的阅读能力提出了较高的要求，对学生综合知识的能力一样如此，学生只有在理解题目意图并顺利建构知识点之间关联的基础上才能顺利解题.因此，教师在复习教学中一定要重视知识点之间的关联并将其纵向、横向之间的联系进行梳理与体现，使学生能够明了知识点间的外在与内在联系并获得解题的第二步突破.例如，贯穿高中整个数学学习过程的函数知识是很多知识点都能与之关联的，教师在具体教学中就应将其经常与其他知识点进行关联性的训练，学生在这种有意义的训练下往往能够更好地对知识点进行重组与概括，知识点的延伸功能也会因此得以更好地彰显，这对于构造法解题来说是极有意义且关键的.

3.培养学生的发散思维

构造法解题还需要学生能够对问题展开多角度的思考，学生的发散性思维在构造法解题过程中的重要性也就非常明显了，因此，教师应从多方面入手对学生的发散思维进行训练.比如，教师应该对数学命题的发散性多加关注，可以对命题的条件、结论进行改变并引导学生在不断的变化中展开积极的思考、归纳与概括，使学生从不同角度对数学本质形成更加深刻而综合的认识.我们数学教师都极为重视的变式训练实质上就是对学生解题方法发散的训练，多角度的研究与解决是培养学生发散思维的重要途径，也是构造法解题训练必不可少的重要手段.

总之，构造法解题对于学生分析问题、解决问题、构造新问题的能力均提出了较高的要求，从其本质讲，这是一种探究与创新思维的体现，学生的学习能力与热情都会因为构造法解题的掌握而获得更好的发展.W