培养学生转化能力的案例探析
☉江苏省扬中高级中学 丁 建
方法、途径众多的数学思想在培养学生数学技能与思维品质上均能发挥重要的作用,着眼于学生最近发展区,巧设认知阶梯,并引导学生进行数学知识转化方法的探究,能使学生在类比、数形、表征、辩证等过程中理解转化的核心、精髓与价值,并在此基础上掌握与运用转化的策略以提升数学能力.
一、类比转化
鲁班因齿形物割伤自己而类比联想锯子的发明,既包含了属性相近的内容,又囊括了本质上的差异.教师应从此类事例中掌握类比转化的教学本质并精心设计问题情境,引导学生在知识生长点上进行观察、分析、比较并最终掌握类比对象本质的方法,使学生最终在思维碰撞的观察、联想与类比中获得新的突破.
案例1 几何概型的计算公式.
问题:如图1,线段AB长3m,P1,P2,P3,P4,P5五点将其分成了六等份,则这五个点中取任意一点到线段AB的两个端点的距离都不小于1m的概率是多少?

图1
(1)本题中的基本事件与总数分别是什么?(取点,总数为5)
(2)假如将“取任意一点到线段AB的两个端点的距离都不小于1m”记作事件A,那么满足事件A的点共有几个?(3个,分别为P2,P3,P4)
(4)这属于哪种概率模型?有何特点?(古典概型,事件中每个基本事件发生的可能性相等及所有基本事件的数量有限是古典模型的两个特点)

图2
(5)将问题进行变化:如图2,线段AB长3m,则在线段AB上任取一点到线段AB的两个端点的距离都不小于1m的概率是多少?
①此处的基本事件与总数又分别如何呢?(取点;线段AB上所有的点)
②各基本事件发生的可能性相等吗?(相等)
③这属于古典概型吗?和古典概型相比可有异同呢?(不属于;各基本事件发生的可能性相等是两者的共同点;不同点是所有基本事件的数量无限)
④假如将“任取一点到AB两个端点的距离都不小于1m”记作事件B,那么满足事件B的点有多少呢?(无数)
⑤在知道基本事件与满足事件B的总数的情况下仍然可以采取古典概型公式进行计算吗?结果应该是多少呢?
⑥“基本事件的总数”和“事件B的个数”分别与线段AB上哪部分的点对应呢?(如图3,将线段AB分成三等份并将中间两点记作C、D,则基本事件的总数为线段AB上的点;满足事件B的总数为线段CD上的点)
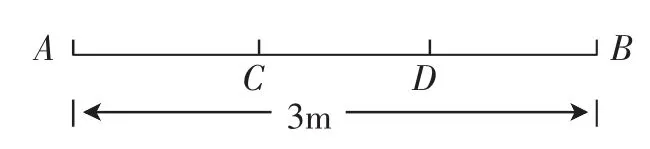
图3
⑦由“无数”转化成“有限”又该怎样变化呢?(假设一份“无数个点”组成每一等份的线段,则基本事件的总数为3份“无数个点”;满足事件B的总数为1份“无数个点”,则
⑧对于此处的1份“无数个点”和3份“无数个点”又该怎样进行抽象概括呢?(1份“无数个点”构成1份“线段的长度”;3份“无数个点”构成3份“线段的长度”)
⑨此处的“线段”是什么量呢?(几何量)
(6)概括(定义、计算公式等略).
引导学生在观察、联想、类比中体验转化的核心环节、转化的方法,以及在何处转化是本案例中的关键.
二、数形转化
突破思维定式并结合形象思维与逻辑思维能使学习者在研究对象的观察与挖掘中进行数与形的联想与转化,因此,教师应善于引导学生进行数形转化并因此锻炼学生观察的敏锐性与思维的灵活性.
案例2已知a>0且a≠1,(fx)=x2-ax,当x∈(-1,1)时均有(fx)<,求实数a的取值范围.
引导学生探究以下问题:
(1)将(fx)=x2-ax代入条件“(fx)<”可以得到什么?(不 等 式x2-ax<)
(2)直接解该不等式可行吗?(有难度)
(3)直接解不等式属于“数”的范畴,那么,从“形”的角度可否解决呢?(很难找到和它对应的图形)
(4)能不能将这一“组合式”拆分成我们熟悉的模型呢?
(5)能否从函数的角度对“f1(x)<f2(x)”进行表征?
生:根据函数图像和不等式的关系可得:在区间I上,f(x)<g(x)⇔函数f(x)的图像在函数g(x)的下方,则问题转化成:a为何值时,在区间(-1,1)上的图像均在f2(x)=ax的图像下方?具体如图4.

图4
引导学生在逐个问题的思考中领略数形转化的方法与精髓,不仅激发了学生的积极态度,也使学生在转化的依据、条件、缘由上进行了更多的思考.
三、表征转化
对于同一个数学对象进行不同的数学表征直至寻得有用的信息往往能够帮助学生有效解题,学会运用不同的数学知识与方法解决同一问题往往也会在不同的表征中实现,因此,教师应善于引导学生在重构问题的表征中获得等价的问题以提升学生思维的灵活性.
案例3 不等式ax2+bx-10<0的解集是{x|-2<x<5},求a、b的值.
分析:学生往往比较习惯于正向思维,因此对于这种需要讨论参数a、b的二次不等式ax2+bx-10<0的求解往往会感觉烦琐,但学生如果能够联想方程、函数、不等式之间的内在联系并从方程的角度对这一问题进行新的表征,该问题很快也就转化成了“方程ax2+bx-10=0的解分别为-2,5”,结合方程的定义或根与系数的关系求得a、b的值也就不难了.
解:由不等式解集的几何含义可知,不等式ax2+bx-10<0的解集为{x|-2<x<5}与方程ax2+bx-10=0的解为-2,5是等价的.由方程根的定义或根与系数的关系可得解得a=1,b=-3.
引导学生运用“方程的根”对“不等式的解集”进行表征是此题化难为简的关键,学生感悟到视觉变化的同时也实现了解题的优化.
四、辩证转化
教师在学生顺向思维受阻之时应及时引导学生转换思维方式并勇于打破常规,引导学生在问题的对立面进行思考并获得解题的简化.
案例4 已知三条抛物线y1=x2+2ax+a2-a+3,y2=2x2-(4a-2)x+2a2-a,y3=x2-(2a+1)x+a2+2中至少有一条和x轴相交,求实数a的取值范围.
分析:与x轴相交的抛物线不止一条这一条件包含了7种不同的情况,如果从问题的正面着手考虑,这7种不同情况的分类讨论就是相当繁杂的,但是如果从反面考虑三条抛物线不与x轴相交,问题则会变得简单许多.
解:设三条抛物线与x轴不相交,则相应判别式均小
引导学生在问题的对立面进行分析与思考能使学生感受到辩证思维答题的巧妙,解题过程变得别开生面的同时也将解题变得更加简单.
数学中的转化思想是一种特别有价值的意识与创新,教师应精心设计启发性的情境并使学生在积极的探索中展开观察、分析、联想与思考,使学生在很多繁难问题的探究中学会类比、数形结合、多元表征与辩证并因此逐渐养成善于运用数学思想的意识与习惯,长此以往,学生的思维与能力必然会获得长足的发展.H

