深度神经网络在船舶自动舵中的应用
李少伟 王胜正

关键词: 自动舵; 深度置信网络; 对比散度算法; 受限波尔兹曼机; 深度神经网络; 反向传播算法
中图分类号: TN830.1?34; U665 文献标识码: A 文章编号: 1004?373X(2018)24?0039?04
Application of deep neural networks in ship autopilot rudder
LI Shaowei1, WANG Shengzheng2
(1. School of Mathematics and Computer Science, Jianghan University, Wuhan 430056, China;
2. Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China)
Abstract: An autopilot rudder control algorithm based on deep belief networks (DBNs) is proposed to improve the control accuracy and self?adaptability of the existing ship autopilot rudder. Each layer of the restricted Boltzmann machine (RBM) model that constitutes the DBN is pre?trained by using the comparative divergence algorithm and combining with the data recorded in the advanced crew examination system of Shanghai Maritime University. The results are taken as initial weight values of deep neural networks. On this basis, the back propagation algorithm is used to conduct fine?tuning training of the multi?layer depth structure. The results of the simulation experiment show that the error between the proposed method and the ship operation simulation of a senior captain is only 5.2%.
Keywords: autopilot rudder; deep belief network; comparative divergence algorithm; restricted Boltzmann machine; deep neural network; back propagation algorithm
0 引 言
随着人工智能的发展,神经网络、模糊算法等方法也在不断地应用于自动舵控制系统中。乔富强利用DSP强大的数字信号处理能力,提出一种基于传统PID算法的自动舵控制方法[1]。由于作者在算法中加入了滤波函数,因此与传统方法相比,其控制精度有了一定的提高。文献[2]建立完整的船舶航向保持控制模型,并引入神经网络方法获取模型参数,以应对船舶在不同风、流条件下的运动。文献[3?4]为了改进传统PID算法中参数调整的难题,提出基于BP神经网络和PID控制算法的自动舵控制方法。该方法根据船舶当前水域的风、流、浪等情况,利用神经网络实时计算得到PID控制参数,提高了自动舵的环境适应能力。为了克服BP神经网络在应用中的缺陷,文献[5?6]提出采用RBF神经网络来代替BP神经网络,进行PID参数的计算。与传统BP神经网络相比,这种控制方法具有更快的训练和学习速度,同时可以对并行数据进行高速处理;为了进一步提高自动舵的智能化程度,文献[7?8]均提出了基于模糊神经网络的船舶自动舵控制算法。这种算法可以利用人类的知识和经验,将自动舵控制算法中的参数以模糊算法进行表示,同时具有在线学习以及自动调整参数等优势,进一步提高了自动舵的实用性;除此以外,科研人员还针对船舶运动模型进行过自动舵的研究,但由于船舶运动受到环境因素影响较大,因此其实用性大大受限[9]。
综上可知,采用人工神經网络来实现自动舵控制算法已经成为此领域的发展趋势与研究热点。但是由于传统的神经网络并不能很好地模仿人脑的工作原理,同时存在梯度扩散、收敛于局部最小值以及不适合无标签数据的处理等问题,使得基于神经网络的自动舵算法存在着控制精度不高、环境适应性不强等问题。DNN模型是对于神经网络模型的一种很好的改进与取代。这种模型可以更为精确地模拟人脑的工作过程,并且更适用于处理类似船舶自动舵控制这样的无标签大数据。文献[10]提出一种训练DNN的方法,称为逐层贪婪算法,开启了学术界和工业界对DNN研究新热潮;文献[11]对深度学习进行了较为全面的综述,提出了贪婪逐层预训练学习过程用于初始化深度学习模型的参数,从底层开始训练每层神经网络形成输入的表示。在此之后,堆栈各层神经网络转换为深度监督前馈神经网络,用梯度下降进行微调。由于深度学习在我国发展较晚,国内相关学者在引进相关算法的同时,对算法进行了更详细的分析与解释。当前,DNN方法已经成功应用于图像识别、语音识别、语种识别等领域,并且已经取得了良好的效果。
至此,将DNN应用于自动舵控制算法的研究已经有了较为坚实的理论基础,但至今为止,在国内外相关文献中尚未发现基于DNN的船舶自动舵控制研究。本文选取DBN作为自动舵控制算法,希望能用此方法改进现有自动舵控制算法中存在的控制精度不高、环境适应性以及稳定性差等问题,是一种创新也可以说是一种挑战。
1 DBN神经网络结构
DBN由若干结构单元堆栈组成,如图1所示,其结构单元通常为RBM[12]。
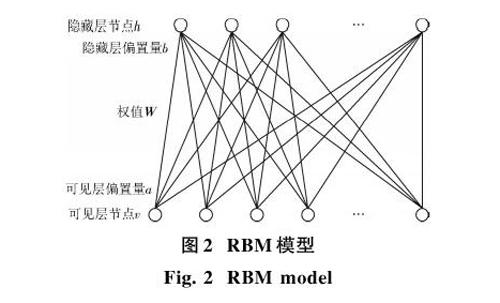
对于图1中的任何一个RBM,其结构均是一个两层结构模型,底层是由可见节点[v=v1,v2,…,vi]组成的可见层,顶层是由隐藏节点[h=h1,h2,…,hj]组成的隐藏层,两层之间的节点全连接,每一个连接都有一个权值[wij],但处于同一层的节点之间互不连接。同时,可见层与隐藏层均有自己的偏置量,记为a,b。每个神经元的输出有两种,分别为0或者1。图2为RBM模型示意图。
DBN模型由多层无监督的RBM和一层有监督的BP网络组成,结合了无监督学习和有监督学习各自的优点。DBN的训练过程分為预训练和微调两个阶段[13]。
为了方便后述实验部分的进行,在此列出基于对比散度算法的RBM模型训练过程。对于模型训练的详细理论基础及推导,可详见文献[13]。
1) 给定训练周期J,学习率η、对比散度算法中的参数K(K=1)以及样本数量[ns]。
2) 初始化权值向量[W]以及偏置量[a,b],初始化ΔW=Δa=Δb。
3) 采用对比散度算法,通过对样本进行循环,更新ΔW,Δa,Δb。
① 利用式(1)计算隐藏层第k个神经元为1的条件概率,即:
[P(hk=1|v)=sigmoidbk+i=1nvi*wik] (1)
[sigmoidbk+i=1nvi*wik]将式(1)中的计算结果与[0,1]之间的随机数r进行比较,若[r<P(hk=1|v)],则[hk]=1,否则取0。最终得到更新后的隐藏层[h0]。
② 利用式(2)计算可视层第k个神经元为1的条件概率,即:
[P(vk=1|h)=sigmoidak+i=1nhi*wik] (2)
将式(2)中的计算结果与[0,1]之间的随机数[r]进行比较,若[r<Pvk=1|h],则[vk]=1,否则取0。最终得到更新后的可视层[v1]。
③ 利用式(3)~式(5)更新[ΔW,Δa,Δb]。
[Δwij=Δwij+[P(hj=1v0)v0i-P(hjv1)v1i]] (3)
[Δai=Δai+(v0i-v1i)] (4)
[Δbj=Δbj+[P(hj=1v0)-P(hjv1)]] (5)
④ 利用算法第①~③步完成对RBM模型的逐层训练。
4) 利用式(6)~式(8)更新网络参数W,a,b。
[W=η1nsΔW] (6)
[a=η1nsΔa] (7)
[b=η1nsΔb] (8)
5) 进入算法步骤2),直到满足训练周期的要求,则算法停止。
按以上方法训练出的参数需要进行反向微调才能达到DBN整体最优效果。反向微调时,DBN利用BP网络有监督地训练最顶层的BP网络,对RBM网络学习到的特征进行分类,将DBN的实际输出与预期输出之间的误差逐层反向传递至所有RBM网络,微调RBM网络层间的参数,得到最优的DBN。



2 建模关键技术
2.1 网络输入参数
影响船舶运动状态的因素很多,在此,根据航海操舵模拟器的设计原理,选取具有较大权重的影响因子,使其作为神经网络的训练输入,例如风向、风力、流向、流速等。由于DBN模型仅能识别0,1两种数据,因此,影响船舶运动的因素全部转换为二进制数值化的形式。
2.2 网络输出参数
DBN的功能和作用就是实现舵角的改变,使船舶尽可能稳定地航行在目标航线上,因此,神经网络的输出参数仅有一个,就是目标舵角。对于普通商船而言,舵角的取值一般在-35°~35°之间,因此,网络的输出取值定位0~71,采用7位二进制表示。
3 模型验证与分析
3.1 模型结构
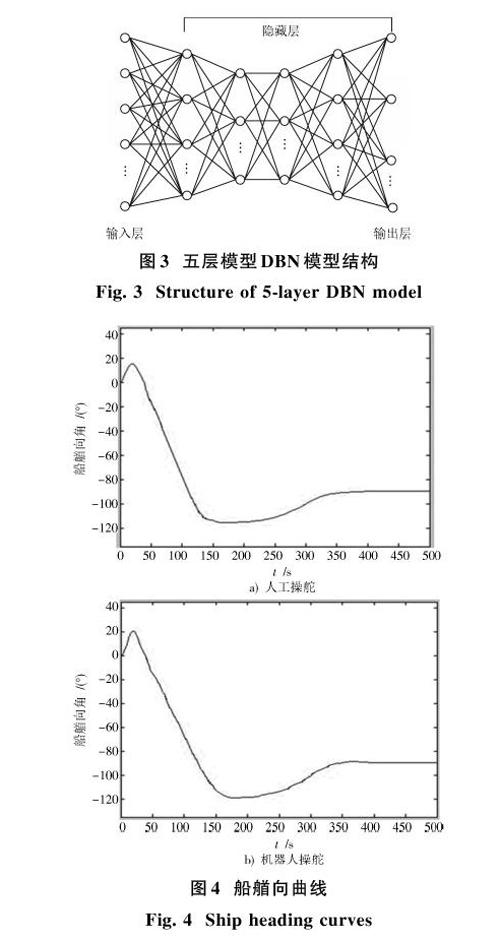
图3展示了使用最为广泛的5层DBN模型。将图3所示的DBN模型为核心,在此基础上,引入DeepLearnToolbox[14]作为开发工具,适当微调隐藏层神经元的数量,以验证不同数量的神经元对DBN模型的影响。
3.2 仿真数据分析与比较
仿真实验中的船舶编号为3号,长度179.7 m,船宽27.6 m,最大吃水9.5 m,船型为集装箱船。操船场景为长江口外锚地进港,数据记录时间为500 s,船艏向初值为0,不涉及避碰与超船。其中人工操舵与自动舵操舵已经分别予以记录,如图4、图5所示。



由圖4及图5可知,机器操船与人工操船在精度上已经非常接近。为了进一步对误差进行分析,选择每秒进行一次误差记录,记为ei,单位为m,并采用式(9)、式(10)得到误差指标。
[E=i=0nein] (9)
[D=i=0n(ei-E)2n] (10)
式中:E表示误差均值;D表示误差的方差。经过计算可知,人工操船的误差为22.5,方差为4.6;机器操船的误差为23.7,方差为5.3。以上数据也进一步说明基于DBN模型的自动舵具有较高的精度。
反观现有的相关控制算法,大部分文章的作者仅仅提出了相关的理论,并没有针对相关理论进行验证或仿真验证,例如参考文献[3?4]所涉及的内容;有的文章虽然进行了仿真实验,但实验环境采用固定参数的形式,并且没有相关船舶运动模型作为支撑,例如参考文献[5?8]中的内容,因此其结果并不具备一定的实用价值。
通过仿真实验可知,本算法在自动舵中的控制精度与人工操舵精度差距已经非常微小,平均误差仅为5.2%,已具备了实船测验的基本条件。本算法同时也存在一定的不足之处,例如对于图6所示的会遇场景,本算法暂无法处理,留待后续研究。
本文针对船舶自动舵控制系统,提出一种基于DBN的船舶自动舵控制模型。该模型隐藏层确定为5层,同时以上海海事大学高级船员培训系统所记录的考试培训数据作为训练样本,结合对比散度算法,对组成DBN模型的每一层RBM依次进行训练,以获得DBN的初值;然后提取出训练样本中实操精度较高的数据作为有标签的数据,采用BP算法实现对DBN的微调。为提高开发效率,将DeepLearnToolbox工具引入本文,实现对DBN模型的快速训练。
参考文献
[1] 乔富强.基于DSP的舰船PID自动舵监控系统的研究[J].舰船科学技术,2017,39(14):127?129.
QIAO Fuqiang. Research on PID automatic rudder monitoring system based on DSP technology [J]. Ship science and technology, 2017, 39(14): 127?129.
[2] KULA K S. Model?based controller for ship track?keeping using neural network [C]// Proceedings of 2nd International Conference on Cybernetics. Gdynia: IEEE, 2015: 178?183.
[3] HUO Xingxing, HU Jiangqiang, YU Ting. Fuzzy PID autopilot for ship steering based on stratification and sub fuzzy controller [J]. Journal of Dalian Maritime University, 2013, 39(4): 71?74.
[4] 常静.基于BP神经网络的PID在船舶自动舵中的应用与研究[J].舰船科学技术,2017,39(6):105?107.
CHANG Jing. Application and research of the fuzzy PID autopilot based on BP neural network [J]. Ship science and technology, 2017, 39(6): 105?107.
[5] WANG Renqiang, ZHAO Yuelin, SUN Jianming. Application of optimized RBF neural network in ship′s autopilot design [C]// Proceedings of IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference. Xian: IEEE, 2017: 1642?1646.
[6] WANG Y Y, NGUYEN H D, CHAI S, et al. Radial basis function neural network based rudder roll stabilization for ship sailing in waves [C]// Proceedings of 5th Australian Control Conference. Gold Coast: IEEE, 2015: 158?163.
[7] WANG M H, YU Y Q, ZENG B. Study of intelligent control system for ship autopilot design [C]// Proceedings of 8th IEEE/ACIS International Conference on Computer and Information Science. Shanghai: IEEE, 2009: 701?705.
[8] WU Y X, XUE M J, WU P J. Study on fuzzy neural network?based ship autopilot [C] // Proceedings of 6th International Conference on Natural Computation. Yantai: IEEE, 2010: 1393?1396.
[9] KAPITANYUK Y A, PROSKURNIKOV A V, CAO M. Optimal controllers for rudder roll damping with an autopilot in the loop [J]. IFAC?papersonline, 2016, 49(23): 562?567.
[10] HINTON G E,OSINDERO S,TEH Y W. A fast learning algorithm for deep belief nets [J]. Neural computation, 2006, 18(7): 1527?1554.
[11] BENGIO Y. Learning deep architectures for AI [J]. Foundations & trends in machine learning, 2009, 2(1): 1?127.
[12] 刘建伟,刘媛,罗雄麟.深度学习研究进展[J].计算机应用研究,2014,31(7):1921?1930.
LIU Jianwei, LIU Yuan, LUO Xionglin. Research and development on deep learning [J]. Application research of computers, 2014, 31(7): 1921?1930.
[13] LAROCHELLE H, BENGIO Y, LOURADOUR J, et al. Exploring strategies for training deep neural networks [J]. Journal of machine learning research, 2009, 10: 1?40.
[14] PALM R B. Deep learn toolbox [EB/OL]. [2018?01?04]. http://www.pudn.com/Download/item/id/3341483.html.

