基于GARCH模型族的中国股市波动率检测
谭 璇
(伦敦玛丽皇后大学 经济与金融学院,英国 伦敦 E1 4NS)
在现代金融理论中,波动率是金融时间序列最重要的特征之一,常被用于度量风险的大小,在金融市场的风险测定和金融衍生品定价方面发挥着巨大的作用。在股票市场中,波动不断变化且具有群聚性。为了更好地模拟和预测股市的波动性,广义自回归条件异方差(GARCH)模型过去30年里在计量经济学中得到了充分发展与广泛应用。其原因在于GARCH模型能更好地解释金融时间序列的尖峰厚尾(leptokurtosis)和波动丛聚性(clustering)的特征。
Engle在1982年提出自回归条件异方差(ARCH)模型,核心思想是残差项的条件方差依赖于它的前期值的大小[1],Bollerslev对ARCH模型进行了延伸,提出广义自回归条件异方差模型GARCH模型[2],但是ARCH和GARCH不能反映非对称性(asymmetry)。为了克服这一弱点,Nelson提出了指数 GARCH(EGARCH)模型[3],Zakoian 加入了解释可能存在的非对称性的附加项,推广了门限自回归条件异方差(TGARCH)模型[4],指出负的冲击往往比相同程度的正的冲击引起的波动更大,这种非对称性是受杠杆效应影响产生的。Engle等人引入了GARCH-M(GARCH-in-mean)模型[5],也即ARCH均值模型,他们把残差项的条件方差特征作为影响序列本身的附加回归因子之一,描述风险溢价随时间变化而变化的特征,以反映预期风险波动的影响程度。
目前国内的股市收益率分析主要集中于对沪深两大交易市场大盘波动率的实证分析。其中,刘璐、张倩运用GARCH模型证明了亚洲地区股票收益率波动存在聚集性和持续性[6]。王博研究了上证指数的收盘价序列,比较了其误差服从正态分布、t分布、GED分布条件下的拟合和预测效果[7]。武倩雯对上证指数的研究,证明了股价指数收益率序列具有时变波动、厚尾和波动性集群等特征[8]。林宇采用误差函数对预测波动状态进行了检验[9]。曹栋应用GARCH-M模型研究了沪深300股票的日收益率,分析了股票市场受外部冲击时的正反馈效应,以及冲击对条件方差和未来股票走势的作用[10]。
笔者在上述研究的基础上,以上证综指和深证成指的收益率为研究对象,分析两个市场的收益率,以GARCH模型族检验国内股票市场的拟合效果,以期为中国股市提供较为准确的波动性预测指导。
一、证券市场收益率波动性的理论分析框架
GARCH模型是专为金融类数据分析设计的模型,是金融学研究中最常用和可行的异方差序列拟合模型,是在ARCH模型的基础上,对误差的方差的进一步建模,在研究股市的波动性方面发挥着巨大作用。GARCH模型假定方差为滞后残差平方的函数,一般由一个条件均值方程和条件方差方程组成。一般认为GARCH(1,1)模型就足以应对日常金融领域的时间序列问题。记扰动项的条件方差为,下标t表示条件方差可以随时间而变。α是ARCH项的阶数,假设依赖于前期扰动项的平方,β是GARCH项的阶数,假设受其自回归阶数的影响。其条件方差表达式为:

门限自回归条件异方差(TARCH)模型,可用来分析数列的剧烈波动性。而条件方差与两个因素有关,一个是前期残差的平方,一个是条件方差。其条件方差表达式为:
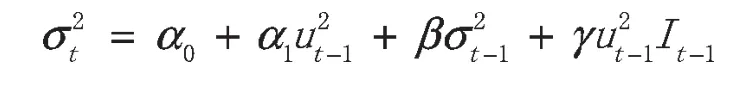
在指数GARCH(EGARCH)模型中,只要等式右侧的γ值不为0,就说明冲击的影响存在非对称性。其中条件方差的表达式为:

GARCH均值模型(GARCH-in-mean)是由Robert等1987年提出,条件方差表示预期风险。如果其条件方差同时满足GARCH(1,1)过程,记收益率为 rt,则一个 GARCH(1,1)-M 模型的均值方程表达式为:

二、中国股市波动的实证分析
(一)样本数据的选取与统计性描述
笔者选取了2013年7月1日到2018年7月1日的上证综合指数(SSEC)和深证成份股指数(SZSE)的收盘价,共有1 221个日数据组成一个时间序列,应用EViews9.0等工具检验股票价格指数的波动。为了减小舍入误差,笔者将上证综指和深证成指的日收盘价进行对数处理,得出的日收益率的表达式为:
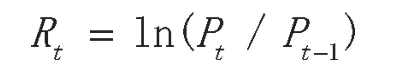
其中Rt代表日收益率,Pt代表当日收盘价,Pt-1代表前日收盘价。上证综指和深证成指的对数收盘价格和收益率走势如图1所示。

图1 上证综指和深证成指的对数日收盘价格和收益率
从图1可以看出,上证综指和深证成指的日收盘价序列在2013年下跌后,2014年持续上升,2015年达到最大值,其后在2015—2016年间波动下跌,2016年后基本保持平稳缓慢上升的态势。上证综指和深证成指的收益率都在0附近频繁上下波动,且在2015—2016年间存在较大的波动,波动的聚集效应明显,即较大的波动后紧跟一个较大的波动。由此可以初步判断二者的收益率存在异方差性,即过去的收益率波动对未来的波动产生影响。
笔者利用EViews工具生成上证综指和深证成指的收益率描述性统计结果,如表1所示。上证综指和深圳成指都有正的平均收益率,且上证综指的平均收益率高于深圳成指,但平均收益率均不显著异于零;两个收益率序列的偏度为-1.26和-0.97,均为负值,存在左偏现象;峰度值为10.52和7.62都远大于3(峰度值为3则为正态分布),可知其收益率序列的分布有明显的“尖峰厚尾”特征。从J-B统计量为3 203.92和1 279.37以及均为0的P值来看,拒绝了收益率序列服从正态分布的原假设。为了建模的正确性,笔者在建模中尝试使用了Student's t分布和Generalized Error分布(GED)来描述它们的尖峰厚尾特征。

?
(二)邹(Chow)突变点检验
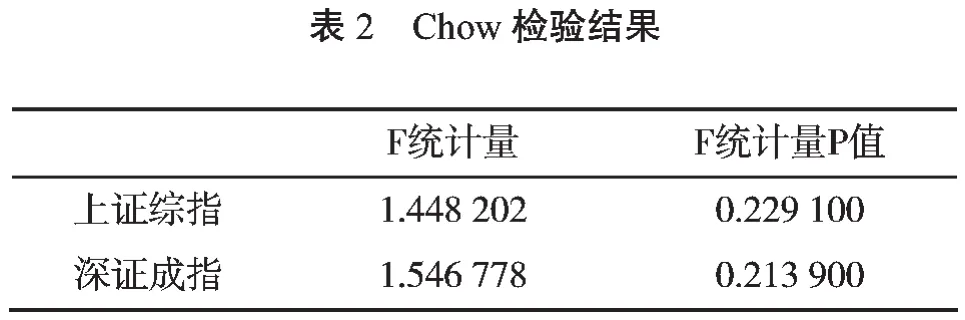
为了使GARCH的建模准确,必须检验收益率序列中是否存在断点和突变,笔者利用EViews工具对收益率序列进行邹(Chow)突变点检验,结果如表2所示。该结果显示突变点检验不能显著拒绝不存在结构变化的原假设,即上证综指和深证成指的收益率序列均不存在结构性突变。
?
(三)平稳性检验
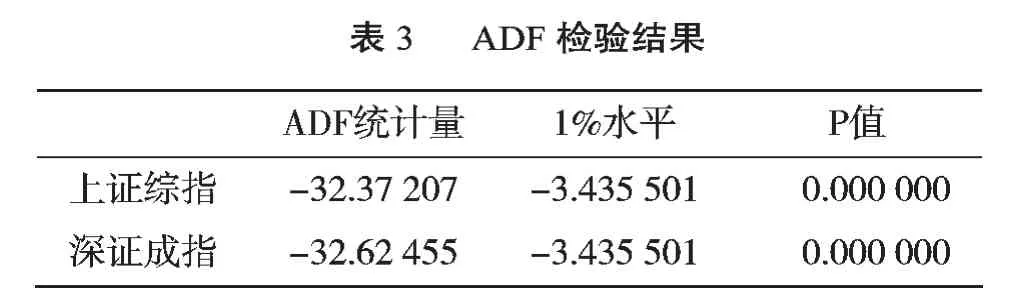
GARCH模型适用于平稳的序列,为了建模的有效性,在建模之前必须进行时间序列的平稳性检验。本文采用金融实证分析中最常用的单位根检验(ADF检验法)对上证综指和深圳成指进行检验,检验结果如表3所示。
?
从表3可知,即使是在1%的置信水平上,ADF检测值都远小于相应的临界值,明确拒绝了原序列存在单位根的原假设。上证综指和深证成指的收益率序列不存在单位根,都是平稳的。
(四)ARCH效应检验
数据是否存在ARCH效应,是建立GARCH模型的前提条件。笔者对上证综指和深证成指的自回归方程的残差进行拉格朗日乘子(ARCH-LM)检测,结果如表4所示。

?
由表4可知,上证综指和深证成指自回归方程的残差F统计量和R方统计量的伴随概率P值均为0,显著拒绝不存在ARCH效应的原假设,用GARCH模型来拟合两个指数的收益率波动是合理的。
(五)模型估计
从笔者对样本数据的描述性统计可知,收益率序列显著拒绝正态分布的假设,因此用Eviews工具尝试对上证综指和深证成指分别建立Student's t分布和 Generalized Error(GED)分布下的GARCH、EGARCH和TARCH模型,生成系数估计结果见表5和表7。

注:*、**和***是指在显著性水平分别为0.1、0.05和0.01时统计显著,()内为正态分布检验值
根据AIC和SC值越小越好,调整R方绝对值和对数似然距离越大越好的原则,以及GARCH模型的系数均为正数且显著进行综合考虑,认为建立GED分布下的GARCH模型对上证综指较为合适,为此,笔者尝试建立 GARCH(1,1)-M 模型,发现其系数在置信度为0.1的情况下没有显著性,因而没有必要建立GARCH(1,1)-M模型。为此,我们对上证综指建立GED分布下的GARCH模型,并由此建立其均值模型和方差模型分别为:


从表5输出的结果看,ARCH项的系数α=0.066 858且显著,表明收益率序列外部冲击对内部有影响,但影响较小,尤其是在短期内不会产生较剧烈的影响。从GARCH项的系数β=0.930 796且显著来看,上一期的方差也会对下一期的方差产生较为显著的影响,但长期内冲击会慢慢减弱,最后趋近于零,即再无影响。从ARCH项与GARCH项的和α+β=0.066 858+0.930 796=0.997 654,非常接近1来看,模型整体趋于平稳,过去的波动率对上证综指有持续性影响。
再对GARCH模型进行ARCH-LM检验,其结果如表6所示。F统计量和R方统计量的伴随概率P值均大于0.05,残差序列已经成功消除ARCH 效应。因此。可以认为 GED-GARCH(1,1)模型较为准确地拟合上证综指的收益率序列。

?
对深证成指收益率序列进行GARCH,EGARCH和TARCH建模分析,结果如表7所示。综合考虑AIC,SC值,调整R方,对数似然距离可以得出结论:对深证成指建立t分布下的GARCH模型较为合适。笔者尝试建立t分布下的GARCH(1,1)-M模型,结果如表8所示,其系数 P值均不超过0.05,所以各项系数均显著。因此,我们对深证成指建立t分布下的GARCH(1,1)-M 模型如下:

注:*、**和***是指在显著性水平分别为0.1、0.05和0.01时统计显著,()内为正态分布检验值


?
由此可见,ARCH项的系数与GARCH项的系数 α+β=0.075 988+0.918 111=0.994 099<1,说明其收益率波动衰减系数小于1但接近1,外部冲击对深证成指股价波动有一定的影响,而且会持续较长时间。从GARCH(1,1)-M的模型检测结果来看,方程中的风险溢价系数为0.161 655,且伴随概率P值为0.032,小于0.05,通过检验,说明预期风险每增加一个百分点,其收益率增加0.161 655个百分点。表明在深圳股票市场,风险和收益率之间存在较为显著的正相关性,这个结论与风险溢出理论相吻合。
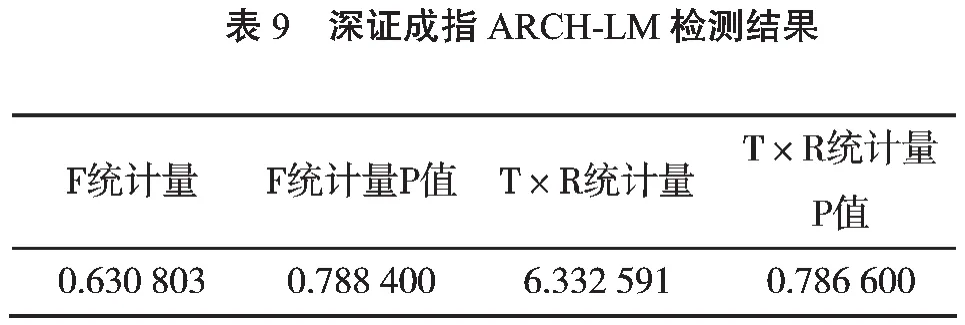
对GARCH(1,1)-M模型进行ARCH-LM检测,其结果如表9所示。F统计量和R方统计量的P值均显著大于0.05,故而在GARCH-M模型中,残差序列已经成功消除ARCH效应,因此t分布下的GARCH(1,1)-M模型可以较为准确地拟合深证成指的收益率序列。
?

图2 上证综指和深证成指的模型预测的条件方差图
(六)模型条件方差图和预测效果检测
笔者对上证综指和深证成指建立GARCH和GARCH-M模型,由Eviews工具生成预测条件方差图,如图2所示。上证综指和深证成指的最大方差均出现在2015—2016年间,超过0.06,并且在2014—2016年出现了三次大幅波动。
根据收益率序列预测的条件方差图可知,上证综指和深证成指的条件方差图具有三个特征:其一,时变性。随时间变化,条件方差的波动也会产生变化。其二,波动聚集性。条件方差的波动具有明显的聚集效应,大的波动之后出现大的波动,小的波动之后出现小的波动。其三,共同运动性。上证综指和深圳成指的各时段波动幅度有很大的相似性,最值出现的时段几乎一致,深圳成指的最值比上证综指稍大,但区别并不明显。上海和深圳股市日收益率序列各时段的条件方差总体来看没有太大区别。
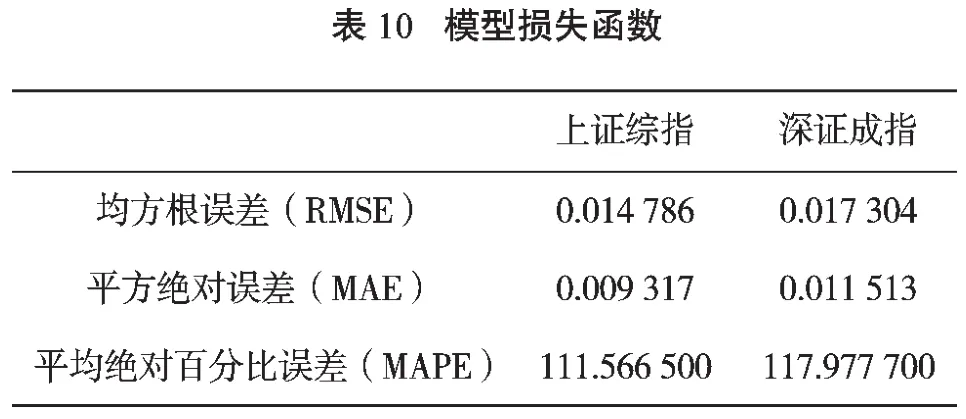
从条件方差图中我们无法准确地判断哪个模型能更好地测量收益率序列的波动性,因此我们采用三种损失函数指标来描述模型对收益率序列的拟合程度。它们分别是均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE),其结果如表10所示。
?
由表10可见,上证综指和深证成指的三种误差值都相对较小,可以说GARCH模型能较好地拟合中国股市的收益率序列的波动性变化。由于上证综指的三个指标数值RMSE、MAE、MAPE都小于深证成指的数值,预测误差较小,可见GARCH模型对上海股票市场有较好的拟合效果。
结 论
笔者将GARCH、TARCH、EGARCH和GARCH-M模型分别应用于上证综指和深证成指进行拟合度测试,建立的模型有效地消除了残差序列的ARCH效应,表明GARCH族模型适用于分析中国股市的波动性。经过简单的描述性统计分析,可以得出中国股市的波动具有聚集特征的结论。这意味着过去的股市波动能影响它的未来走势;上证综指和深证成指的收益率序列平稳且不符合正态分布,呈“尖峰厚尾”特征。
中国股票市场指数的波动具有持续性和收敛性的特征。在对上证综指和深证成指建立TARCH和EGARCH模型分析时,其相应的估计参数如表5和表7所示,它们的不对称信息系数均不显著,表明沪深股市在统计上不存在杠杆效应。国外学者对成熟股票市场的分析表明,成熟股票市场普遍存在波动性不对称、股票价格波动的影响负面冲击比正面冲击更大的现象。而沪深股市的不对称系数不显著,与世界上大多成熟的股票市场存在杠杆效应的实际情况不一致。
上海和深圳证券交易所的股票缺乏杠杆效应,可能与没有卖空机制有关。当有利空消息时,尽管投资者预计股价会进一步下跌,但只有持有股票的投资者能对利空做出反应,其余投资者不能进行卖空操作。此外,中国股市作为一个新兴市场,其信息发布、信息处理和信息传输渠道存在诸多不足,导致股市波动幅度大于成熟股票市场;市场交易者的行为也存在许多不合理性,大量的噪声交易使得股票市场价格波动剧烈,从而使不对称信息对股市的影响不太显著。
与成熟的股票市场相比,中国股市的确还存在一些问题,因此需要各方共同努力,促进其健康成长。一方面,完善证券立法、严格证券执法,加强监管,提高信息披露透明度,减少人为因素造成的暴力波动。另一方面,尽早引入卖空机制,为投资者提供多元化投资和避险工具,促进证券市场健康发展,使其在优化资源配置方面发挥更大作用,助力中国经济转型发展。

