含双馈式风机的电力系统分岔研究

郭镇齐，李汝男,谢 征，郭 峰

(国网鞍山供电公司，辽宁 鞍山 114001)

目前，随着清洁能源的大规模利用，风力发电已经成为能源并网的主力。但是，随机波动所造成的不确定性也给风力发电的利用带来一定困扰[1-2]。而双馈式风机作为风机的主要机型之一，研究其并网运行时给系统带来的影响也成为一项重要课题[3]。

双馈式风机在并网运行时所造成的影响与其他类型的风机相比有很大区别，这也引发一些学者的关注[4-6]。一直以来，静态模型都是分析电力系统变化的主要模型。但是，由于双馈式风机的数学模型为非线性动态方程，用静态方法研究其特征时，计算结果会与实际运行结论有所不同。因此，为了更精确地描述其动态特性，一些学者利用分岔理论来更精确地描述双馈式风机并网的影响[7]。在文献[8-9]中，作者分别利用负荷侧的无功功率和系统的有功功率2个参数进行分岔分析，并计算出几种分岔点。本文通过设定负荷侧的无功功率变化来分析系统电压的稳定性。

1 双馈式风机的数学模型

电力系统动态电压数学模型一般为

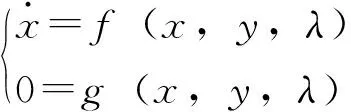
(1)

式中：x∈Rn和y∈Rn分别为系统的微分变量和代数变量；式(1)包含电压变化的潮流过程和动态过程。

1.1 风机的两质块轴系模型

本文采用风力发电机的两质块轴系模型来研究风机的动态变化[10-13]。发电机转子、定子控制变量约束如下：

(2)

式中：θt为扭转角位移；ωt为发电机旋转角速度；ωr为风力机轴的旋转角速度；Tsh为轴系的扭转转矩；Te为发电机的输出电磁转矩；Tm为风力机的机械转矩；Ht为风机的惯性常数；Hg为发电机的惯性常数；B为发电机转子阻尼系数。

(3)

式中：Ksh为轴系的刚度系数；Dsh为风机的阻尼系数；PDFIG为风机传输到系统的有功功率；ρ为风机所处地区的空气密度；R为风机叶轮半径；Vw为风机运行风速；Cp为风机的风能转换系数。

1.2 发电机的电磁暂态模型

a.风机侧发电机模型

由于风力电机电磁暂态持续时间很短，本文在简化转子、定子电磁暂态过程情况下，推导出定子和转子侧电压电流关系式为

(4)

(5)

式中：ψs为定子磁链且大小近似等于Us/ωs；Idrref为d轴转子电流分量的参考值；Kpω为发电机的转速比例调节系数。得出风机注入系统的功率为

(6)

b．节点1并联的等值发电机

采用发电机的二阶模型：

(7)

式中：M为发电机惯量;Dm为阻尼系数；Tm1为发电机输入转矩。

1.3 负荷模型

本文采用电机动态特性综合负荷模型，其能够反映静态和动态负荷各自的特性，形成Walve负荷模型[14]，其数学表达式为

(8)

式中：UL和δL分别为负荷节点的电压和相角；p0为负荷有功功率的恒定部分；q0为负荷无功功率的恒定部分；p1、p2、p3、q1、q2、q3均为负荷系数。

1.4 电网络模型

网络提供给负荷的功率为

(9)

通过以上各部分模型的联立，可以得出风机系统的综合模型。本文选择θt、ωt、ωr、δL、UL作为系统电压分析的微分变量；UL、θ作为系统电压分析的代数变量；q0作为系统的分岔参数。

2 算例分析

本文选择的系统如图1所示。节点1为二阶发电机；节点2为双馈式风机与用户负荷；节点3为并网的无限大系统。详细参数和说明见文献[15-16]。本文选择分岔分析软件AUTO 07来进行分岔类型的分析。

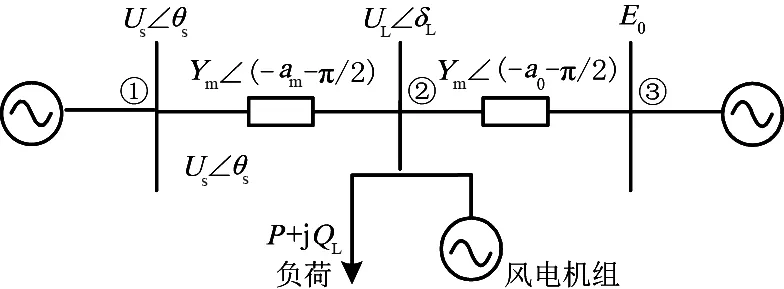
图1 系统模型

a.双馈风力发电机组参数

ωs=1 pu，Rs=0.007 06 pu，Ls=3.671 pu,Rr=0.005 pu，Lr=3.656 pu，Lm=3.5 pu，Hg=0.5 s，B=0.01 pu，Ht=3 s，Ksh=0.5，Dsh=0.01，R=82.5 m，Idrref=0.286，Kpω=100。

b.等值发电机参数

M=0.3，Dm=0.05，Tm2=1.0。

c.动态负荷参数

p0=0.6，p1=0.4，p2=0.3，p3=2.55，q1=-0.03，

q2=-2.8，q3=2.1。

d.网络参数

Y0=20，Ym=5，am=-5，a0=-5，E0=1.0，Us=1.0。

2.1 风速为5 m/s时的分岔分析

图2中点1为系统的初始运行位置。表1为风速是5 m/s时QL—UL曲线数据值。根据软件程序设定，分析图2，QL—UL曲线为实线时,代表系统处于稳定状态。QL—UL曲线为虚线时，代表系统处于不稳定状态。当电压发生Hopf分岔时，QL—UL曲线上会出现“■”。当电压出现静分岔点时，QL—UL曲线上会出现“□”。QL—UL曲线的拐点代表系统出现鞍结分岔点。

随着负荷侧无功功率的提高，系统图上出现“□”标志，表示此时系统出现了静分岔。由此可见，当QL<1.68 pu时，系统电压始终在一个稳定运行的范围。说明在低风速下，随着负荷侧无功功率的增大，电压稳定的抵御能力较强。

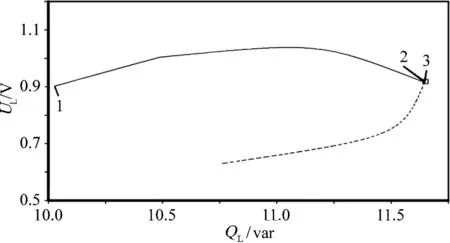
图2 风速为5 m/s时系统分岔图

图2中标号负荷无功功率/var 负荷节点电压幅值/V12310.0511.6811.680.900.920.92

2.2 风速为10 m/s时的分岔分析

图3中点1为系统初始运行位置。 表2为风速是10 m/s时QL—UL曲线数据值。点2处出现了“■”，点3处为QL—UL曲线的拐点。由图3可以看出，系统电压在负荷侧无功功率增大过程中，发生Hopf分岔和鞍结分岔。当QL=11.17 pu时，QL—UL曲线已经由实线转化为虚线。此时已不能简单分析鞍结分岔，而要考虑系统在出现Hopf分岔时已经失稳，系统可以承受负荷侧的无功功率极限已经有所降低。

图3 风速为10 m/s时系统的分岔图

图3中标号负荷无功功率/var负荷节点电压幅值/V1210.0511.170.901.01311.700.84

2.3 风速为11 m/s时的分岔分析

图4中点1为系统初始运行位置。表3风速为11 m/s时QL—UL曲线数据值。随着负荷侧无功功率的增大，QL—UL曲线在点3处出现了fold分岔。从图4可以看出，在系统电压运行到功率极限之前，出现fold分岔。在该风速下，系统能够承受的最大无功功率仅为QL=11.12 pu。fold分岔意味着系统的潮流方程已经无解，在静态模型上已经达到了其运行极限[17]。

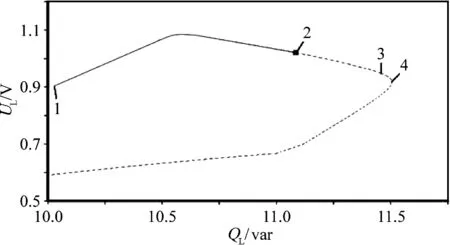
图4 风速为11 m/s时系统的分岔图

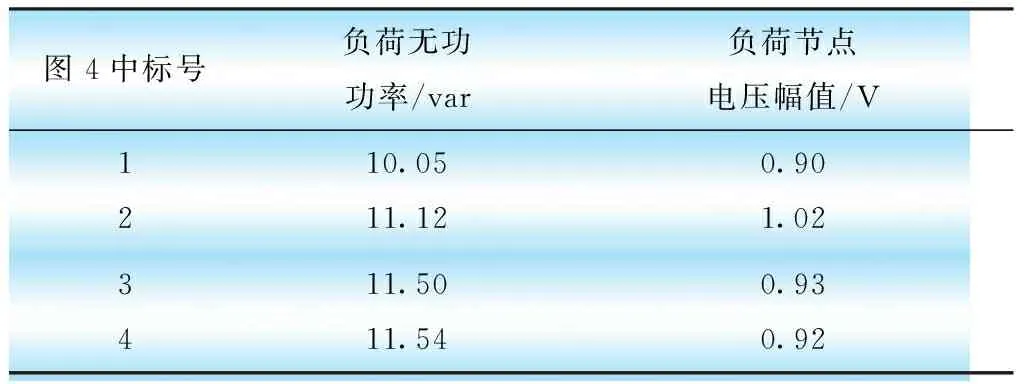
图4中标号负荷无功功率/var 负荷节点电压幅值/V1210.0511.120.901.023411.5011.540.930.92

2.4 风速为12 m/s时的分岔分析

图5中点1为系统初始运行位置。表4为风速是12 m/s时QL—UL曲线数据值。点2处出现“■”。由图5可以看出，在系统QL—UL曲线运行到鞍结分岔点之前，系统已经发生Hopf分岔。在系统发生鞍结分岔失稳之前，其电压已经发生动态Hopf分岔失稳。由表4可见，系统失稳时QL=11.06 pu。这个值要远远小于系统本该发生静态失稳时QL=11.45 pu。

图5 风速为12 m/s时系统的分岔图

图5中标号负荷无功功率/var 负荷节点电压幅值/V1210.0511.060.901.01311.450.92

对比表1—表4可以看出，风速越大，系统QL—UL曲线对应的稳定状态下无功功率值就越小，风机系统对电压失稳的抵御能力也就越弱，表明风机运行的动态特性。

3 结束语

在一定的风速区间内，随着风速不断加大，风机能够发出的有功功率越多，经济效益就越高。但是，随着有功功率的不断增大，负荷侧所需要保持稳定的无功功率的需求也在增大。因此，为了保证风机并网时电压的稳定，负荷侧不仅要提高无功功率的裕度，还需要对设备进行容量的增加，以防功率的提升对其造成机械影响。