基于最小偏差的组合权重模型在水资源应急管理能力评价中的应用

郭 亮

(辽宁省葫芦岛水文局，辽宁 葫芦岛 125000)

我国水资源分布规律受人类社会活动和全球气候变化影响已发生明显的改变，季节性及区域性干旱等事件频繁发生，因干旱缺水所造成的自然灾害已对社会经济发展和水资源循环系统构成严重威胁；我国水污染事件受船舶污染或企业违法超标排污等影响频繁发生，造成社会生产和城市生活供水的中断，严重影社会经济的发展和居民的正常生活[1]。建立完善的应急管理体系是应对水资源突发事件的有效方法，对应急环节进行科学合理的安排将直接决定了应急行动的效率和突发事件的危害程度[2]。合理的评价指标体系的构建不仅可提高应急行动的效率和能力，而且有利于促进对水资源应急管理的科学合理评价和突发事件控制技术的提升，从而降低干旱事故的概率和危害[3]。据此，本文以辽宁省大凌河水资源应急管理为例，通过构建基于最小偏差的组合权重评价模型对其应急管理能力进行综合的评价分析，以期为提高应急管理能力和突发事件控制技术提供一些理论依据[4]。

1 构建水资源应急管理能力评价指标体系

评价指标的科学性、上下级指标的层次性以及同级指标之间的相互独立性，是构建水资源应急管理评价指标体系的重要基础和依据，通常可采用最小均方差法、Delphi法和相关系数法进行判别[5]。本研究结合研究区域水资源应急管理的基本特征和内涵，利用Delphi法筛选出具有代表性的18个二级评价指标和4个一级指标。为了提高评价结果的准确性并便于专家的评价赋分，在进行评价需对模糊性评价指标进行详细的描述说明，构建的评价指标体系见表1。表中B1～B4分别代表应急预防能力、应急准备能力、应急响应能力和应急恢复能力；C11～C14分别代表危险源识别与评价、应急监测能力、应急预警能力和法律规章制度；C21～C26分别代表应急队伍见啥、预案建设、教育培训、演练、备用水源建设以及应急保障能力；C31～CC33分别代表应急处置能力、指挥协调能力、信息沟通能力；C41～C45分别代表善后处置能力、事故分析总结、预案的完善度、事故的后续跟踪监测和奖惩责任追究。

2 基于最小偏差的组合权重评价模型

对水资源管理能力的薄弱环节进行准确查找并加强应急能力建设、完善应急管理体系是进行水资源应急管理能力评价分析的主要目的[6]。要实现对水资源应急能力的客观、科学评价，不仅要构建科学、有效的评价指标体系，且评价模或评价方法的选择将直接决定评价真实性和可靠性。

表1 水资源应急管理评价指标体系

2.1 改进熵权法的客观赋权法

熵权法是以信息熵理论为基础对指标的权重进行客观赋权的方法，信息熵值理论是以系统中的无序化程度为标准，对各指标的离散程度赋予响应的数值，其数值的大小即代表了评价指标在整个评价过程中所占的权重比例即所赋予的熵权值，采用信息熵值法是获取系统中有效信息和数据值的主要方法。熵值的大小即代表了指标的差异性程度，值越大则指标的差异性越小其所包含的有效信息就越少，对综合评价的贡献率就越低相应的指标权重系数越小；反之，则指标所包含的有效信息越大其权重系数就越大[7]。

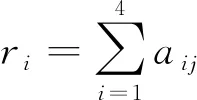
(1)构建判别矩阵。在建立初始判别矩阵的基础上利用下述差值公式构建最终判别矩阵，差值公式如下：

(1)

式中，aij—评价要素i与j的相对重要性标度；ri、rj—分别为评价要素i与j的相对重要性权重。

因各评价要素之间的量纲和单位存在差异，对上述公式进行标准化归一处理，设定Pij为第i个评价目标的第j项评价指标，则其计算公式为：

(2)

(2)对评价指标的熵值ej利用信息熵公式计算。可采用微观分子方式对系统的熵值进行统一计算，假设n1、n2分别代表二元系统中两种物质的分子个数，则该系统的熵值可采用Botlgman公式计算：

(3)

式中，Ω—微观角度的两种物质的分子排列方式。

总熵值计算：

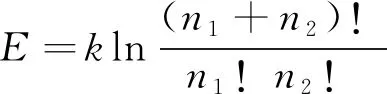
(4)

单位熵值计算：

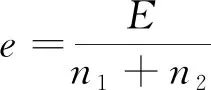
(5)

(6)

第j项评价指标的熵权可采用下式进行计算：

(7)

2.2 G1法的主观赋权法

G1序关系法、G2法和AHP层次分析法是主观赋权法的主要方法，G1法相对于AHP层次赋权法，无需对判断矩阵的一致性进行检验，可明显提高计算效率和速度，并且可不考虑相同层次权重的元素个数；而相对于G2赋权法，G1法具有简单、方便的优点，且有利于提高专家风险意识的判别[8- 10]。G1序关系法对指标权重系数的计算与过程如下：

(2)对xi指标的权重系数wi进行计算，引入wk-1/wk作为评价指标xk-1与xk的重要性程度之比，rk;k=m，m-1，，2作为比值的理性，其取值范围见表2。m值较大值rk值可取1。评价指标的权重wm计算公式如下：

(8)

wk-1=riwi;k=m，m-1，，2

(9)

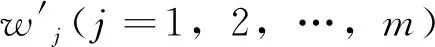
表2 rk参考赋值及含义

(10)

式中，bij—各评价指标的数值。

2.3 最小偏差的组合权重

熵权法主要是对指标信息的内在联系进行客观的描述，但往往忽略了决策者对主观信息的判断，并以此可能对评价结果造成严重的偏差；而G1法虽然考虑了决策者的主观判断且可操作性较强，但往往因决策主体的知识经验或个人偏好的不同引起评价结果的不同。综合集成上述两种方法可同时考虑主、客观判别对信息作用并避免单一赋权对权重系数造成的误差，通常采用的方法为线性加权法，然而该方法需要确定主观偏好系数并因此造成评价结果具有一定的主观判断性[11]。因此，本研究对指标的综合权重采用最小偏差法进行综合计算。

设定指标权重计算方法共有q中，其中主观、客观法分别有l和q-l种，则权重向量表示为：

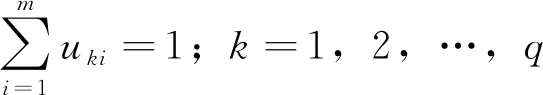
(11)

利用偏差函数对决策的客观性和决策者的主观意见进行综合考虑，并使得各方法求得的权重偏差最小，其权重向量为w={ω1，ω2，，ωm}T，所构建的单目标优化模型可采用下式进行表示：

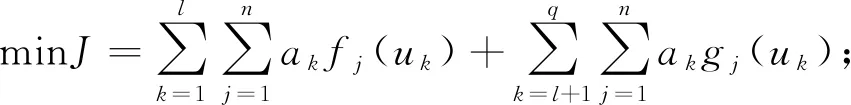
(12)

式中，ak—利用各赋权法求得的权重系数；aj—利用第j中赋权法求得的权重；fj(uk)、gj(uk)—分别为主、客观赋权法的偏差函数。

各赋权法的权重偏差越小则所代表所求得的权重信息的有效利用率越高，因此所构建的模型可转化为：

然而，正如凯登 (Gerald Caiden)所说，公共行政本当服务社会，造福人类。曾几何时，在不少地方，它竟已沦落成“邪恶，残忍，道德败坏，公理荡然无存，无辜惨遭杀戳的工具，而数以千计的公务员却对之非但熟视无睹，甚至参与其中，随波逐流”(Caiden，2007:260)。行政道德何在?行政道德改革已是刻不容缓，迫在眉睫。

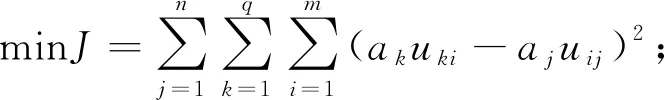
(13)

在此基础上可建立Lagrange函数，表达式为：

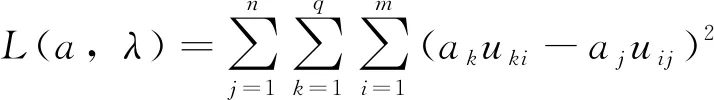
(14)

式中，λ—构建函数所引入的参数。

结合Lagrange函数极值存在的必要条件，L即为建立的Lagrange函数，对其进行微分求解有：

(15)

该线性方程组系数行列式利用克莱姆法则分析有唯一的解，并可求得各赋权法的权重系数，通过各权重系数与相应方法的指标权重进行加权最终可求得各赋权方法的权重值。通过计算应急管理评价指标的权重可利用专家打分法对各指标的评分进行赋值，并求得应急管理能力的综合评价值E，公式如下：

(16)

式中，ωi、ωij—分别为各一级、二级评价指标的权重；Sij—目前条件下，各二级评价指标的评分值。

3 实例应用

3.1 研究区域概况

大凌河流域位于辽宁省西部，流域大小支干交错，全长398km，所占面积约为2.35万km2，是辽宁省重要的生活用水及工农业用水的主要来源之一，属于典型的河网水系地区；纵横交错的河道是流域进行蓄水和输水的主要方法和途径，因此造成的蓄水调控能力较低极易引起汛期弃水和夏季枯水的现象[12]。据此，该地区为了确保突发性供水危机发生时可以进行正常供水编制了水资源综合规划，在水资源配置和保护、节水规划、蓄水预测以及应急水源等方面开展了深入的研究和调查；而且，该区域还针对水环境安全预警和警情发布做了系统的规划，对突发性水污染事件制定专项应急预案，分别从预警监测、应急响应、措施保证、责任追究与奖惩等方面开展工作；对应急预案进行定期的培训教育和应急演练，并定期进行经验总结和汇报，不断完善源体制和内容[13]。本文研究结合该区域应急管理具体状况，采用专家打分法分别对各评价指标进行赋分，结果见表3。

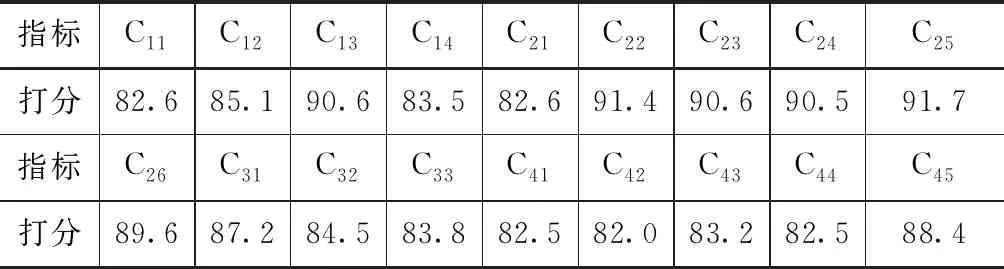
表3 大凌河流域某地区应急预案各评价指标专家打分结果

由表3打分结果可知，专家对部分指标的打分偏低，由此表明，该区域的应急管理能力还存在一定的不足例如应急管理法规规章制度还有待进一步完善，危险源评估和识别等工作有待加强，应急队伍建设还存在不足，对于事故的分析总结、善后处置以及后续跟踪监测等方面仍有待进一步的提升和加强。

3.2 水资源应急管理能力评估

结合各评价指标的内涵和相关研究成果可将其评价等级划分为5个等级即差、较差、一般、较好、好。考虑到评价集模糊性基本属性，采用百分值对各上述评价集进行定量化给分，并以此提高计算的效率，引入V={100，80，60，40，20}，各评价等级标准和取值范围见表4。

表4 评价等级标准及取值范围

首先采用改进的熵权法对一级指标构建初始判别矩阵，并对4个指标之间的相对重要性权重进行计算，然后利用差值法和文中所述计算公式构建最终的判别矩阵，一级指标判别矩阵计算结果见表5。

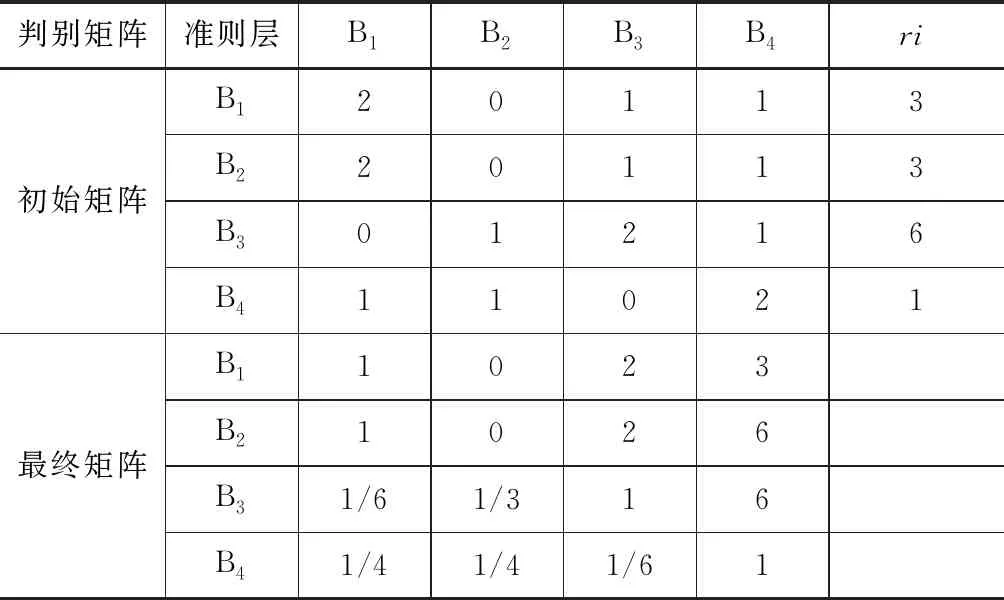
表5 评价指标体系中一级指标的初始、最终判别矩阵

利用文中所述计算公式对评价指标体系各级指标的熵和熵权进行计算，其中一级指标计算结果为：

eB=(0.830，0.830，0.781，0.880)

ωB=(0.251，0.251，0.320，0.172)

二级指标的计算结果分别为：

eC=(0.753，0.776，0.672，0.871，0.801，0.772，0.782，0.806，0.715，0.772，0.801，0.720，0.854，0.778，0.778，0.635，0.782，0.804)

ωC=(0.065，0.060，0.091，0.032，0.036，0.045，0.040，0.040，0.052，0.041，0.102，0.145，0.078，0.031，0.031，0.055，0.028，0.026)

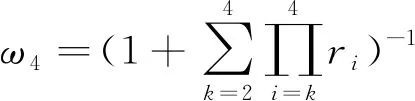
ωC=(0.071，0.058，0.105，0.042，0.031，0.042，0.026，0.020，0.058，0.053，0.112，0.138，0.080，0.036，0.032，0.052，0.025，0.018)

利用G1法和改进的熵权法可构建评价指标体系准则层的权重矩阵，如下所示：

利用公式(15)则有：

对G1法和改进的熵权法进行权重计算，结果为α=(0.59，0.41)，其中λ为-0.405。因此评价指标体系准则层的权重w*=(0.260，0.244，0.326，0.170)T，各二级指标权重计算结果如下所示：

w*C=(0.070，0.060，0.093，0.037，0.036，0.042，0.034，0.031，0.056，0.045，0.108，0.142，0.075，0.032，0.034，0.051，0.028，0.025)

利用文中所述公式(16)对各二级指标的评分值和权重值进行计算，求得评价值结果见表6。利用表6中数据可对大凌河流域应急管理能力评价值E进行求解，其中E1～E4计算结果分别为86.5、89.2、85.5、82.4，E值为86.1，评价结果显示处于“好”水平。由此说明该大凌河流域水资源应急管理能力整体处于较好的水平等级。

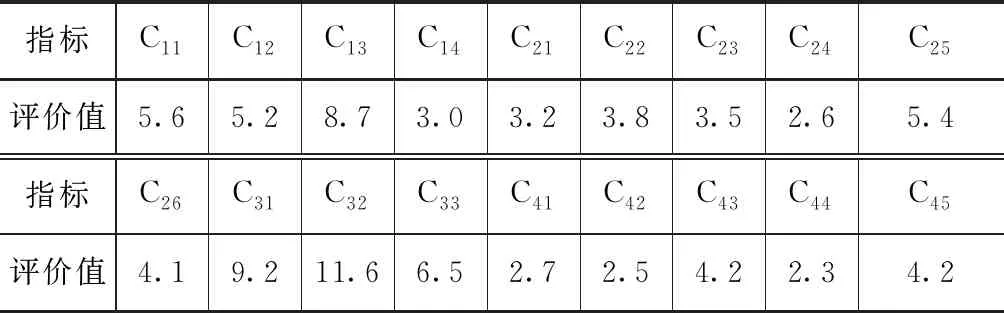
表6 评价指标体系各二级指标值

评价指标体系中各一级指标均处于“好”的等级水平，应急响应、防控和准备能力应处于相对更好的水平，而对于应急恢复能力建设表现出相对滞后状态[13]。本文针对研究区域水资源应急管理实际状况分别对应急预防、准备、响应和恢复建设方面提出了以下几条建议，以期提高研究区域的水资源应急管理水平：定期对危险源进行识别和评估，对潜在的重大危险源进行定期的检查和排除；加强水资源应急管理人才的引进，加快人才队伍建设；完善应急信息处理系统和通信系统建设，促进应急响应机制建设；加强应急处置后的教育培训和经验分析总结，对现有应急预案提出建议并不断完善，提升对应急处置结束后水质变化的跟踪监测能力，确保事故不会再次发生[14]。

4 结论

本文分析了G1法和改进赋权法基本理论和适用范围，通过将二者进行有效的结合建立了基于最小偏差组合权重评价模型，以辽宁省大凌河流域某地区为研究对象进行水资源应急管理能力的综合评估，得出的主要结论如下：

(1)对影响应急管理能力的各因素采用数值法进行直观的对比表征，进而可定量的分析研究区域的应急管理能力，可为研究区域提高应急管理能力和突发事件控制技术提供一定的理论依据。

(2)研究区域评价指标体系中各一级指标均处于“好”的等级水平，应急响应、防控和准备能力应处于相对更好的水平，而对于应急恢复能力建设表现出相对滞后状态。

(3)影响应急管理能力评估的因素较多，且各因素之间相互作用，关系复杂。本研究所考虑的因素还不够具体和系统，因此对水资源应急管理能力进行科学、精确的评价仍需要更多的因素和理论做进一步的研究。