使用小波分析的水下机器人多传感器故障检测
,,
(1.沈阳理工大学 自动化与电气工程学院,沈阳 110159;2.中国科学院沈阳自动化研究所)
引 言
水下机器人能更好地帮助我们探索未知的水下世界,最大化地减少人员伤亡,但是,当机器人在水下作业传感器发生故障时,采集的信息必然有误差,如果可以使用一种系统实时进行监测,当传感器发生故障时,及时对它进行恢复处理,不仅能提高作业效率,而且对探索任务有重大意义。目前的传感器故障诊断技术有解析冗余法、硬件冗余法、卡尔曼滤波器法、支持向量机法、专家系统等智能化方法,其诊断方法都需要依赖数学模型,计算量大,实现起来较为困难。本文主要利用小波变换[1-3]的研究方法,解决水下机器人传感器故障问题,根据数据分析及实验结果,验证了机器人在水下作业的传感器故障检测中采用小波分析方法的有效性及准确性。
1 小波分析的基本原理
小波变换包含连续小波变换和离散小波变换[4]。小波变换有两个变量:scale和translation。scale控制小波函数的收缩,其导数为频率,translation控制小波的平移,平移量对应时间。小波变换原理类似傅里叶变换,只是把三角函数换成了小波基,通过信号的伸缩平移可以得到某种重合情况,这样积分也会得到一个极大值,不同的是得到频率成份的同时还可以知道频率的时间位置。
1.1 小波的多分辨率阐述
小波的一个思想是在时间和频率两个方面提供有效的局部化,另一个中心思想是多分辨率,即信号分解是按照不同分辨率细节一层一层进行的。函数f(x)是信号空间L2(R)的空间元素,那么f(x)∈L2(R),且f(x)可以通过信号空间中一组基底表示出来,并且这个基底是可以设置的,选取的基空间等级越高,分辨率就越高。
1.2 多分辨分析方程
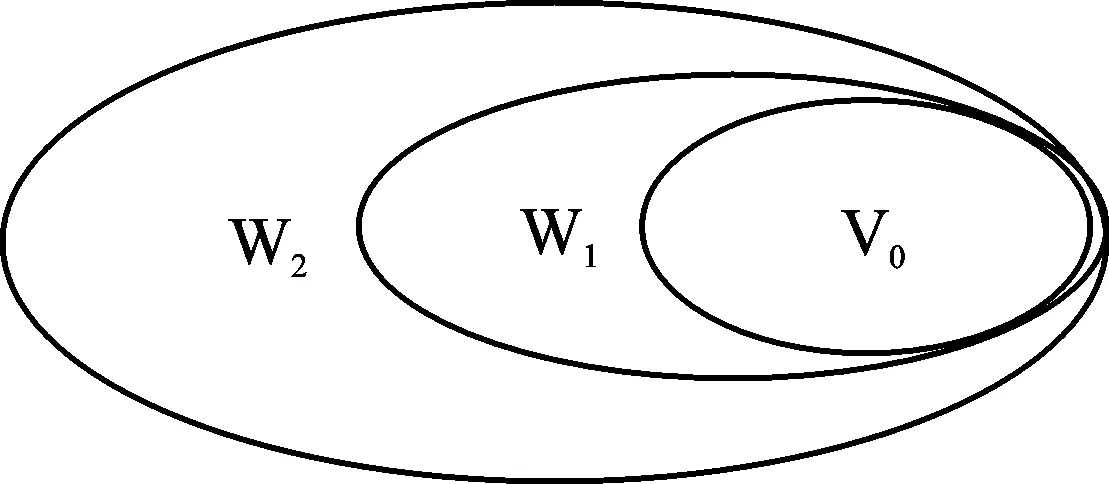
图1 尺度空间
多分辨分析方程[5]就是力求构造两两正交的小波基,来构成高度接近信号空间L2(R),多分辨分析方程只对低分辨空间信号进行处理,高频空间信号不仅可以通过该空间的基地组合起来,还可以通过其低频空间的信号基地组合起来得出高频空间。
如图1所示,初始空间的尺度是任意的(V0),可以选择较高分辨率空间,W1、W2…等表示一个个较细的分辨率函数不停加入,从而会得到更多细节信息。
即对任意函数f(x)属于L2(R),可以表示为:
式中j表示尺度空间,j=1表示空间V0,j=2表示空间V1即W1+V0,k∈z用来完成小波平移变换的参数,φk(t)表示选取的初始空间,φj,k(t)表示每层空间的细节信息。
1.3 小波的离散化
对于连续小波而言,尺度、时间和与时间有关的偏移量都是连续的。如果利用计算机计算,就必须对它们进行离散化处理,得到离散小波变换。
① 离散小波变换定义为:
一般取a0=2,则a=2j,τ=2jkτ0,则采样间隔为j=0,1,2,3,…,k∈z,τ=2jτ0。一般情况下会将τ0归一化,即τ0=1,于是有:
j=0,1,2,3,…,k∈z
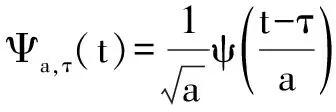
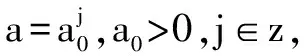
b. 位移离散化:
通常对τ进行均匀离散取值,以覆盖整个时间轴,τ满足Nyquist采样定理。在a=2j时,沿τ轴的响应采样间隔是τ=2jτ0,在a0=2的情况下,j增加1,则尺度a增加一倍,对应频率减小一半,此时采样率可降低一半而不会导致引起信息丢失。
2 传感器数据处理
在现实中,由于机器人旋转方向由人的意向决定,角度有可能会在某一度数内来回摆动,或者沿着某一方向一直走,其角度变化是及其微小的。沿着直线走角度十分相近的这些角,需要通过数据处理来排除,而左右摇摆造成的摆动角,可以看做“噪声”,整个小波就是含噪小波,噪声成分则分布在整个小波域内。这里需要采用阈值函数进行去噪,通过调整系数,不仅要尽可能地保证有效小波的完整性,还要最大程度地去除噪声小波,并且最大程度地减小信号去噪前后的误差。
在实际处理中,用预计达到的深度与机器人实际运动的深度做差值,根据这个差值来进行数据分析,从而判断传感器是否出现故障。在实际操作中,可以在机器人上安装多个传感器,用它们之间的差值来进行数据分析。由于差值无法确定使用几阶小波基来处理,所以选取db1~db7的小波基分别对数据进行处理,得到如图2所示的波形,第一个波形为原始噪声信号,第二个到最后一个波形依次为使用db1~db7小波基进行阈值去噪处理后的信号。
观察处理后的图片,可以看出二阶小波和四阶小波在检测故障时出现较大的延时,不利于检测故障,五阶小波处理故障时波动较大,不利于判断故障点。一阶、三阶、六阶、七阶小波在处理此信号时无法看出哪一种小波处理效果相对较好,因此下面增加信号的复杂度来进一步加以验证。
在这里选取了硬阈值[6]处理方法,只要找出出现故障的点即可满足需求,而不需要对数据进行平滑处理,所以不选用软阈值处理方法[7]。软阈值处理方法不仅不会立刻找出故障点[8],反而会延迟发现故障点的时间。
使用软阈值处理数据,得到如图3所示的数据信息。通过图片可以直观地看出,使用软阈值处理数据时,无论选用哪一种小波基来处理信号,处理后的波形图都有较大波动,不利于找出故障点,进一步说明了需要使用硬阈值方法来快速找出故障,从而减少损失。
3 稳定性验证
为了进一步分析选用哪一种小波基可以保证故障点检测的稳定性,将信号的合理数据与误差数据交替显示,以此增加信号的复杂度,从而检验出哪一种小波基还能稳定地检测出故障点。通过实验得出如图4所示的数据图,从图中可以看出,一阶、四阶和七阶小波在第一处故障点出现较大延时,二阶小波在第三处故障点出现较大延时,五阶小波在处理数据时不稳定,波动较大,六阶小波相对于三阶小波在故障出现时波动较缓,不利于识别故障点。三阶小波处理数据时,在故障点处有明显的凸出,较好地体现出故障点,因此,三阶小波的数据处理相对于其他几阶小波,有着较高的准确性、稳定性和高效性。
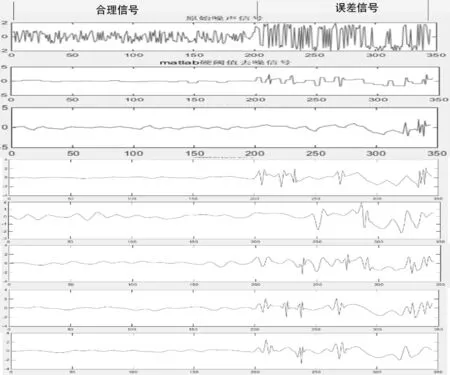
图2 硬阈值处理
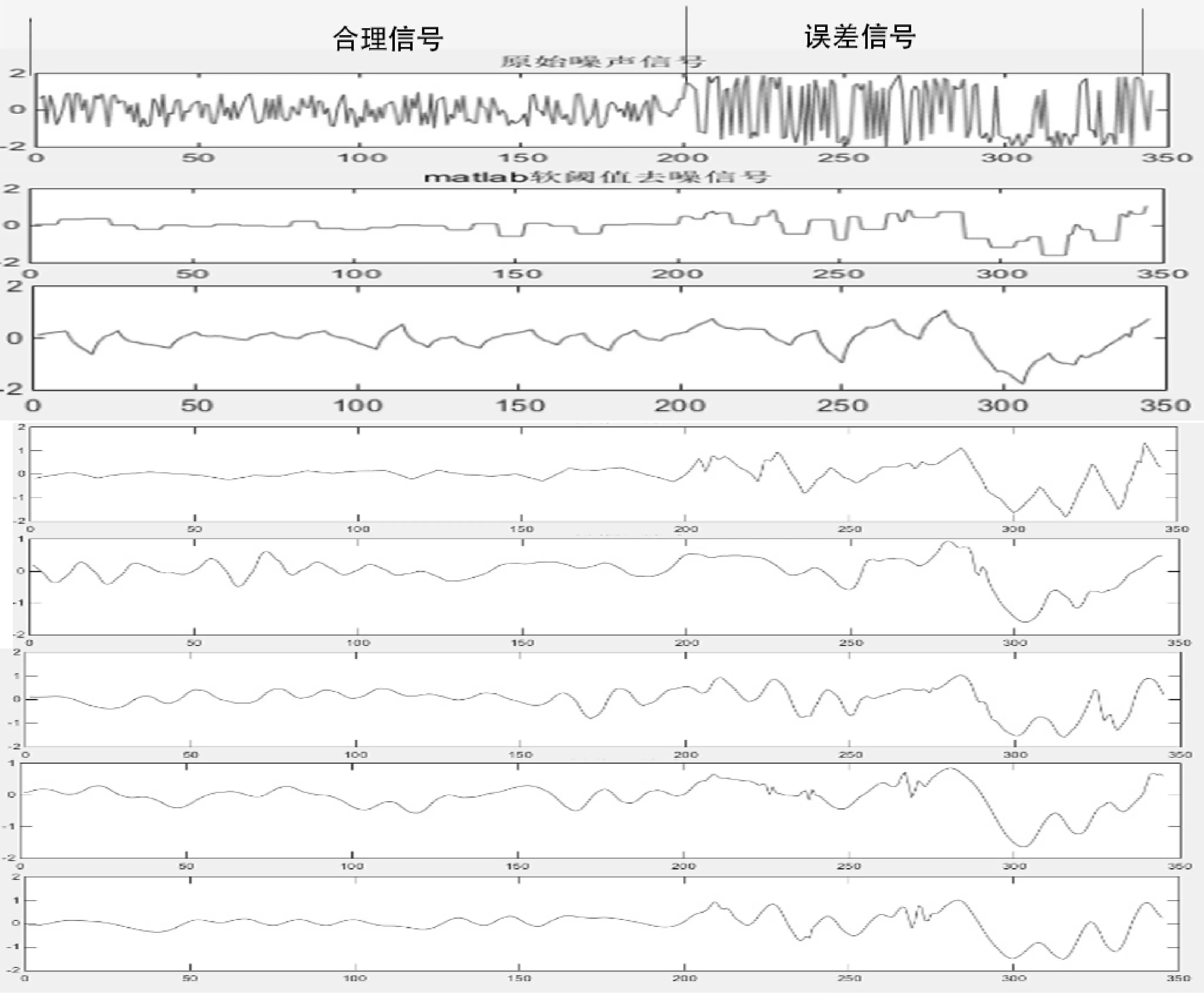
图3 软阈值处理
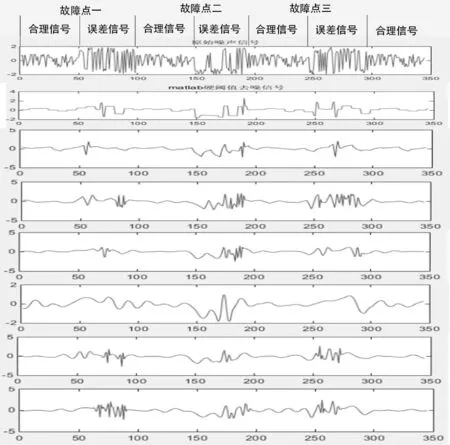
图4 稳定性验证
结 语


