基于三支概念格合并的决策背景规则提取

王一宾，杨思春

(1. 安庆师范大学计算机与信息学院 安徽 安庆 246011；2. 安徽省智能感知与计算重点实验室 安徽 安庆 246011；3. 安徽工业大学计算机科学与技术学院 安徽 马鞍山 243032)

作为形式概念分析(FCA)的核心数据结构，概念格刻画了概念之间的泛化和例化关系，在数据挖掘、机器学习和信息检索等领域取得了广泛的应用[1]。近年来，概念格研究取得了很多重要的成果，特别是文献[2]提出粗糙集框架下的概念格理论以来，一些学者借鉴粗糙集理论深入研究概念格的属性约简和规则提取等问题。文献[3-6]研究了粗糙集与信息系统的属性约简和规则提取问题，文献[7-10]探讨了粗糙集与概念格的属性约简理论以及基于概念格的决策形式背景规则获取问题。文献[11-12]针对不完备决策形式背景，研究了相应的近似概念构造、规则提取以及知识约简。

作为二支决策的推广，三支决策(3-way decisions)是文献[13]提出的一种新的决策理论框架，它将决策问题分为三类：接收、拒绝和不承诺。传统的形式概念分析仅支持二支决策，实际构造形式概念时，仅仅考虑“某些对象共同具有哪些属性”或“某些属性为哪些对象所共同具有”，而没有同时考虑“某些对象共同不具有哪些属性”或“某些属性为哪些对象所共同不具有”。为了更好地支持实际应用中的复杂决策问题，文献[14-15]引入三支决策思想，将具有二支决策的形式概念分析推广为支持三支决策的三支概念分析(3-way concept analysis)，提出了两种具体的三支概念格(对象导出三支概念格和属性导出三支概念格)，并研究了它们与经典概念格之间的关系。

自文献[14]提出三支概念格以来，就引起了有关学者的关注，并取得了一些初步的研究成果。文献[16]对概念格与三支决策相结合的研究历程、研究内容以及研究展望进行了系统的综述。目前，这些工作主要集中在基于三支概念格的属性约简方面[17]，在基于三支概念格的规则提取方面则偏少。文献[18]在利用三支概念格进行规则提取方面做了有益的尝试，给出了基于属性导出三支概念格的决策背景规则提取方法，并通过与经典概念格下的生成规则进行比较，表明了基于属性导出三支概念格的决策背景规则提取方法的有效性和优越性。

本文在文献[18]的基础上进一步研究基于对象导出三支概念格的规则提取，并与经典概念格及属性导出三支概念格下的生成规则进行比较。同时通过对象导出三支概念格和属性导出三支概念格的合并，进一步改善三支概念格下的生成规则质量。

1 基本概念和性质

先给出形式背景及其算子的定义。

定义 1[1](G,M,I)为形式背景，其中G={x1, x2, …,xn}，每个xi(i≤n)称为对象；M={a1, a2, …, am}，每个aj(j≤m)称为属性；对于x∈G与a∈M，如果(x,a)∈I，则称对象x拥有属性a。

定义 2[1](G,M,I)为形式背景，X⊆G，A⊆M。一对算子定义如下：

*: P(G)→P(M)，X*={a∈M |∀x∈X，(x,a)∈I}；

*: P(M)→P(G)，A*={x∈G |∀a∈M，(x,a)∈I}。基于形式背景的算子，可定义形式概念及其概念格。

定义 3[1](G,M,I)为形式背景，若X*=A且A*=X，则称(X,A)是一个概念。X称为该概念的外延，A称为该概念的内涵。

对于任意概念(X1,A1)，(X2,A2)，定义偏序关系为(X1,A1)≤(X2,A2)⇔X1⊆X2⇔A2⊆A1，则形式背景(G,M,I)的所有概念在该偏序关系下是完备格，称为概念格，记为L(G,M,I)。

以下给出概念格之间的细于关系以及决策形式背景及其协调性的定义。

定义 4[8]L(G,M,I)与L(G,N,J)是两个概念格，若对∀(Y,B)∈L(G,N,J)，存在(X,A)∈L(G,M,I)，使得X=Y，则称L(G,M,I)细于L(G,N,J)，记作L(G,M,I)≤L(G,N,J) 。

定义 5[8](G,M,I)与(G,N,J)是两个形式背景，则称(G,M,I,N,J)是决策形式背景。若L(G,M,I)≤L(G,N,J)，则称该决策形式背景是协调的。

为了在形式概念分析中引入三支决策的思想，给出形式背景负算子的定义：

定义 6[14](G,M,I)是形式背景，对于X⊆G，A⊆M，一对负算子定义如下：

*－: P(G)→P(M)：X*－= {a∈M|∀x∈X，(xIa)}={a∈M|∀x∈X，xIca}，其中Ic=(G×M)-I。

*－: P(M)→P(G)：A*－={x∈G|∀a∈A，(xIa)}={x∈G|∀a∈A，xIca}。

在形式背景算子及负算子的基础上，可定义形式背景的三支算子：

定义 7[14](G,M,I)是形式背景，X⊆G，A⊆M，一对三支算子定义如下：

≤: P(G)→DP(M)：X≤=(X*，X*－)

≤: P(M)→DP(G)：A≤=(A*，A*－)

进一步地，可定义上述三支算子的逆运算：

≥: DP(M)→P(G)：(A,B)≥={x∈G|x∈A*且x∈B*－}=A*∩B*－

≥: DP(G)→P(M)：(X,Y)≥={a∈M|a∈X*且 a∈Y*－}=X*∩Y*－

基于形式背景的三支算子，可定义对象导出三支概念和对象导出三支概念格。

定义 8[14]设(G,M,I)是形式背景，(X,(A,B))称为对象导出三支概念，简称OE-概念，这里 X≤=(A,B)且(A,B)≥=X，其中X⊆G，A、B⊆M。X和(A,B)分别称为OE-概念的外延和内涵。

对于(X,(A,B))，(Y,(C,D))，定义偏序关系(X,(A,B))≤(Y,(C,D))⇔X⊆Y⇔(C,D)⊆(A,B)，形式背景(G,M,I)的所有OE-概念在该偏序关系下是完备格，称为对象导出三支概念格，记为OEL(G,M,I)。

类似地，可定义属性导出三支概念及属性导出三支概念格。

定义 9[14]设(G,M,I)是形式背景，则称((X,Y),A)为属性导出三支概念，简称AE-概念，这里(X,Y)≥=A且A≤=(X,Y)，其中X、Y⊆G，A⊆M。(X,Y)和A分别称为AE-概念的外延和内涵。

对于((X,Y),A),((Z,W),B)，定义偏序关系((X,Y),A)≤((Z,W),B)⇔(X,Y)⊆(Z,W) ⇔B⊆A，形式背景(G,M,I)的所有AE-概念在该偏序关系下是完备格，称为属性导出三支概念格，记AEL(G,M,I)。

文献[18]定义了属性导出三支概念格之间的细于关系，以及决策背景基于属性导出三支概念格的协调性。

定义 10[18]设AEL(G,M,I)与AEL(G,N,J) 是属性导出三支概念格。若对于任意((Z,W),B)∈AEL(G,N,J)，存在((X,Y),A)∈AEL(G,M,I)，使得X=Z且Y=W，则称AEL(G,M,I) 细于AEL(G,N,J)，记作AEL(G,M,I)≤AEL(G,N,J)，并称决策背景(G,M,I,N,J)是基于属性导出三支概念格协调的。

文献[18]比较了属性导出三支概念格和经典概念格下的规则提取。

定理 1[18]设(G,M,I,N,J)是决策形式背景，且AEL(G,M,I)≤AEL(G,N,J)。R表示经典概念格下的生成规则集合，TRa表示属性导出三支概念格下的生成规则集合，则R⊆TRa。

定理 2[18]设(G,M,I,N,J)是决策形式背景，且AEL(G,M,I)≤AEL(G,N,J)，R表示经典概念格下的生成规则集合，TRa表示属性导出三支概念格下的生成规则集合，则对于A→B∈R，总存在C→B∈TRa，且C⊆A。

2 基于对象导出三支概念格的决策背景规则提取

文献[18]给出基于属性导出三支概念格的决策背景规则提取方法，本文在其基础上进一步研究基于对象导出三支概念格的规则提取，并与经典概念格及属性导出三支概念格下的规则提取进行比较。

2.1 对象导出三支概念格下的生成规则

先定义对象导出三支概念格之间的细于关系，以及决策背景基于对象导出三支概念格的协调性。

定义 11 设OEL(G,M,I)与OEL(G,N,J)是对象导出三支概念格，若对于任意(Y,(C,D))∈OEL(G,N,J)，存在(X,(A,B))∈OEL(G,M,I)，使得X=Y，则称OEL(G,M,I)细于OEL(G,N,J)，记作OEL(G,M,I)≤OEL(G,N,J)，并称决策背景(G,M,I,N,J)是基于对象导出三支概念格协调的。

例1：表1是一个决策形式背景[18]，G={1,2,3,4}，M={a,b,c,d,e,f}，N={g,h,k}，其对象导出三支概念格OEL(G,M,I)和OEL(G,N,J)分别如图1、图2所示。

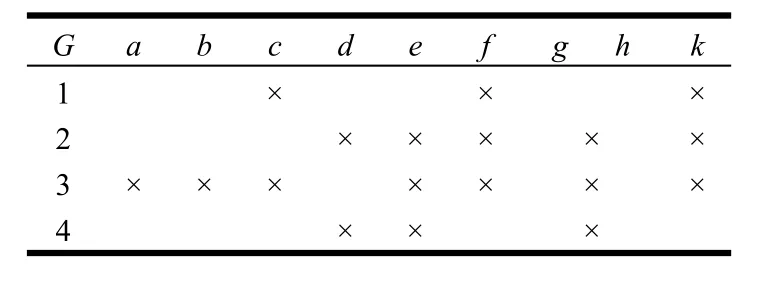
表1 决策形式背景(G,M,I,N,J)

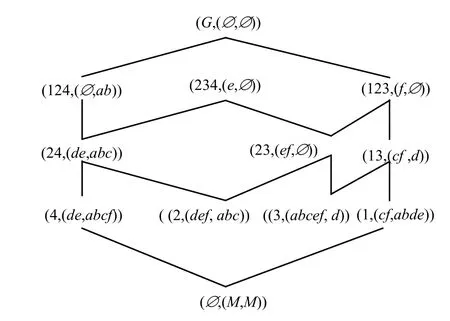
图1 对象导出三支概念格OEL(G,M,I)

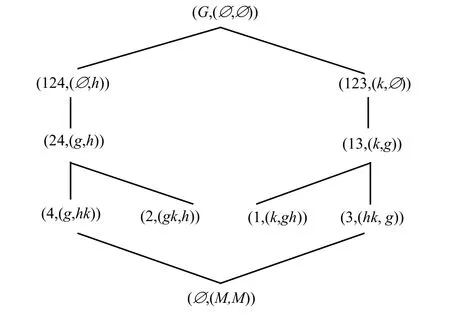
图2 对象导出三支概念格OEL(G,N,J)

由图1、图2可以看出，OEL(G,M,I)≤OEL(G,N,J)，所以表1所示决策背景是基于对象导出三支概念格协调的。

接着定义对象导出三支概念格下的生成规则。

定义 12 设决策背景(G,M,I,N,J)是基于对象导出三支概念格协调的，若对于X、Y≠∅，G，有(X,(A,B))∈OEL(G,M,I), (Y,(C,D))∈OEL(G,N,J), 且X=Y，则称A→C和B→D分别是一个规则。

例2：根据定义12，表1所示决策背景在对象导出三支概念格下的生成规则集合TRo为：

d→g；de→g；ab→h；abc→h；f→k；def→gk；abde→gh；abcf→hk；abcef→hk

2.2 与经典概念格下的生成规则比较

2.2.1 经典概念格下的生成规则

定义 13 设决策背景(G,M,I,N,J)是协调的，若对于X,Y≠∅,G，有(X,A)∈L(G,M,I)，(Y,B)∈L(G,N,J)，且X=Y，则称A→B是一个规则。

例3：表1所示决策背景的概念格L(G,M,I)和L(G,N,J)分别如图3、图4所示。

根据定义13，表1所示决策背景在经典概念格下的生成规则集合R为：de→g；f→k；def→gk；abcef→hk

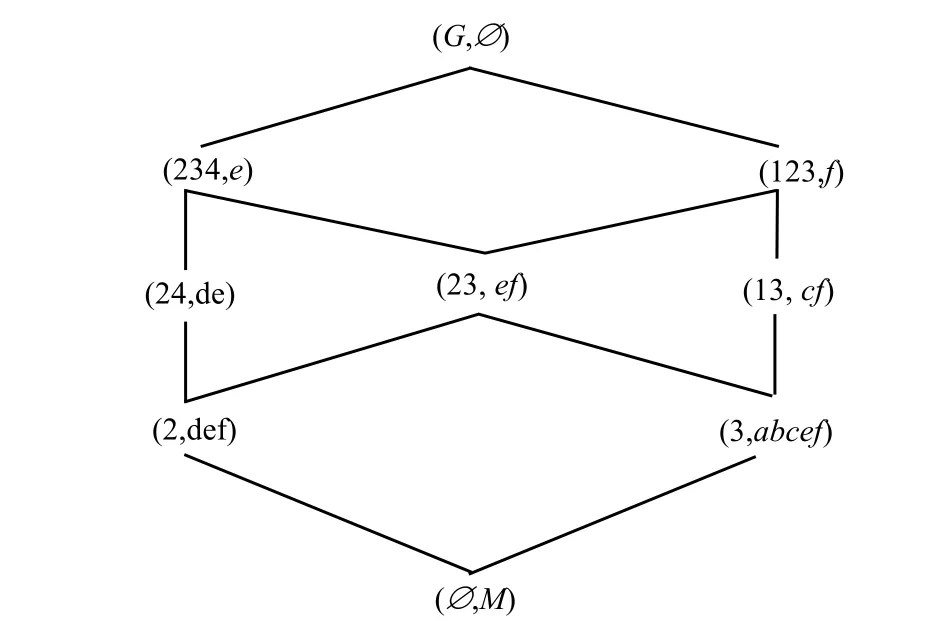
图3 概念格L(G,M,I)

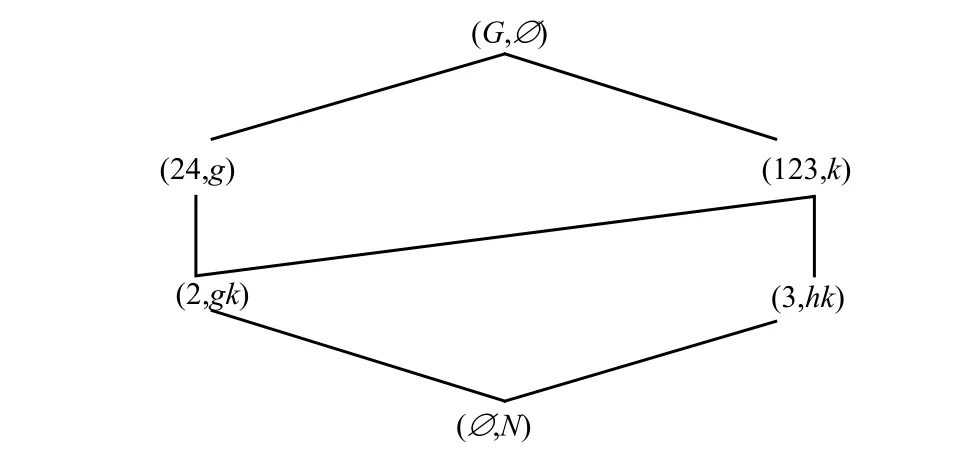
图4 概念格L(G,N,J)

2.2.2 与经典概念格下的生成规则比较

定理 3 设(G,M,I,N,J)是决策形式背景，且OEL(G,M,I)≤OEL(G,N,J)。R表示经典概念格下的生成规则集合，TRo表示对象导出三支概念格下的生成规则集合，则R⊆TRo

证明：对任意A→B∈R，由定义13，存在(X,A)∈L(G,M,I)，(Y,B)∈L(G,N,J)，且X=Y。又因为OEL(G,M,I)≤OEL(G,N,J)，由定义11，对于(Y,(B,Y*-J))∈OEL(G,N,J)，存在(X,(C,X*-I))∈OEL(G,M,I)。由于C=X*I=A，所以(X,(C,X*-I))即(X,(A,X*-I))。由定义12，A→B∈TRo，因此R⊆TRo

例4：比较表1所示决策背景分别在对象导出三支概念格及经典概念格下的生成规则集合TRo和R，可以看出，TRo不仅包含了R中每条规则，还包含了ab→h；abde→gh等其他更多规则。

定理 4 设(G,M,I,N,J)是决策形式背景，且OEL(G,M,I)≤OEL(G,N,J)，R表示经典概念格下的生成规则集合，TRo表示对象导出三支概念格下的生成规则集合，则对于A→B∈R，总存在C→B∈TRo，且C⊆A。

证明：对任意A→B∈R，由定义13，存在(X,A)∈L(G,M,I)，(Y,B)∈L(G,N,J)，且X=Y。由于存在保序 嵌 入[15]ϕ:L(G,M,I)→OEL(G,M,I)，ϕ:L(G,N,J)→OEL(G,N,J)，使ϕ((X,A))=(X,(A,X*-I))，ϕ((Y,B))= (Y,(B,Y*-J))，且OEL(G,M,I)≤OEL(G,N,J)，因此对于(Y,(B,Y*-J))∈OEL(G,N,J)，存在(Y,(C,Y*-I))∈OEL(G,M,I)，使得C→B∈TRa。又因为Y=C*I∩ Y*-I*-I，所以Y⊆C*I，进而C⊆Y*I=X*I=A，即C⊆A。

例5：比较表1所示决策背景分别在对象导出三支概念格及经典概念格下的生成规则集合TRo和R，可以看出，对于R中的每条规则A→B，在TRo中总存在相应的规则C→B，且C⊆A。

与经典概念格下的生成规则比较，对象导出三支概念格下的生成规则更为丰富也更为精炼。但是，由于对象导出三支概念格比经典概念格的概念数量更多，结构也更为复杂，因此构建对象导出三支概念格比构建经典概念格要付出更多的时间开销。

2.3 与属性导出三支概念格下的生成规则比较

2.3.1 属性导出三支概念格下的生成规则

定义 14 设决策背景(G,M,I,N,J)是基于属性导出三支概念格协调的，若(X,Y)、(Z,W) ≠(∅,∅)、(G,G)，有((X,Y),A)∈AEL(G,M,I)，((Z,W),B)∈AEL(G,N,J)，且X=Z、Y⊆W，则称A→B是一个规则。

例6：表1所示决策背景的属性导出三支概念格AEL(G,M,I)和AEL(G,N,J)如图5、图6所示。

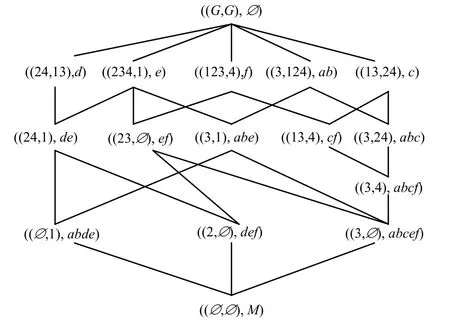
图5 属性导出三支概念格AEL(G,M,I)

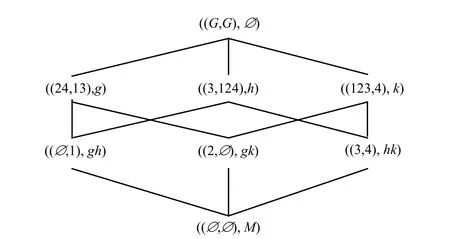
图6 属性导出三支概念格AEL(G,N,J)

根据定义14，表1所示决策背景在属性导出三支概念格下的生成规则集合TRa为：

d→g；de→g；ab→h；abe→h；abc→h；abcf→h；abcef→h；f→k；def→gk；abde→gh；abcf→hk；abcef→hk

2.3.2 与属性导出三支概念格下的生成规则比较

先定义对象导出三支概念格与属性导出三支概念格之间的细于关系，以及决策背景基于对象导出三支概念格和属性导出三支概念格的协调性。

定义 15 设(G,M,I)是形式背景，若对于任意(X,(A,B))∈OEL(G,M,I)，存在((Y,Z),C)∈AEL (G,M,I)，使得X=Y或Z，则称AEL(G,M,I)细于OEL(G,M,I)，记作AEL(G,M,I)≤OEL(G,M,I)，并称形式背景(G,M,I)是基于AEL(G,M,I)和OEL(G,M,I)协调的。

例7：由定义15，对于图1所示对象导出三支概念格OEL(G,M,I)，图5所示属性导出三支概念格AEL(G,M,I)，有AEL(G,M,I)≤OEL(G,M,I)，所以形式背景(G,M,I)是基于AEL(G,M,I)和OEL(G,M,I)协调的；类似地，对于图2所示对象导出三支概念格OEL(G,N,J)，图4所示属性导出三支概念格AEL(G,N,J)，有AEL(G,N,J)≤OEL(G,N,J)，所以形式背景(G,N,J)是基于AEL(G,N,J)和OEL(G,N,J)协调的。

接下来，给出相应的规则定义。

定义 16 设形式背景(G,M,I)是基于AEL(G,M,I)和OEL(G,M,I)协调的，若对于X≠∅、G，(Y,Z)≠(∅, ∅)、(G,G)，有(X,(A,B))∈OEL(G,M,I)，((Y,Z),C)∈AEL(G,M,I)，且X=Y或Z，则称A→B是一个规则。

在上述定义的基础上，以下比较对象导出三支概念格与属性导出三支概念格下的生成规则。

定理 5 设(G,M,I,N,J)是决策背景，且AEL(G,M,I)≤AEL(G,N,J)，OEL(G,M,I)≤OEL(G,N,J),AEL(G,M,I)≤OEL(G,N,J)，则TRo⊆TRa

证明：对于任意A→B∈TRo，由定义12，存在(X,(A,C)∈OEL(G,M,I)，(X,(B,D)∈OEL(G,N,J)。因为AEL(G,M,I)≤OEL(G,N,J)，因此对于(X,(B,D)∈OEL(G,N,J)，存在((X,Z),A)或((Y,X),A)∈AEL(G,M,I)。又因为AEL(G,N,J)≤OEL(G,N,J)，所以(X,(B,D)∈OEL(G,N,J)等价于((X,Z),A)或((Y,X),A)∈AEL(G,N,J)，因此对于((X,Z),A)或((Y,X),A)∈AEL(G,N,J)，存在((X,Z),A)或((Y,X),A)∈AEL(G,M,I)。因此A→B∈TRa，即TRo⊆TRa

例8：比较表1所示决策背景分别在对象导出三支概念格及属性导出三支概念格下的生成规则集合TRo和TRa，可以看出，TRa不仅包含了TRo中每条规则，还包含了abe→h；abcf→h；abcef→h等规则。

通过与属性导出三支概念格下的生成规则进行比较，可以看出，属性导出三支概念格下的生成规则更为丰富。但是，属性导出三支概念格比对象导出三支概念格生成了更多的冗余规则，如图5、图6所示属性导出三支概念格生成了de→g、abc→h、abe→h、abcf→h、abcef→h、abcef→hk等6条冗余规则，而图1、图2所示对象导出三支概念格只生成了de→g、abc→h、abcef→hk等3条冗余规则。因此，在支持决策分析方面，属性导出三支概念格的能力要稍弱于对象导出三支概念格。

3 基于三支概念格合并的决策背景规则提取

与属性导出三支概念格类似，对象导出三支概念格下的生成规则中也引入了一些冗余规则。冗余规则是指[18]，对规则B→C和B′→C′，若B⊆B′且C′⊆C，则称规则B′→C′是冗余的。例如，由图5、图6，属性导出三支概念格下的生成规则中de→g、abc→h、abe→h、abcf→h、abcef→h、abcef→hk均为冗余规则；由图1、图2，对象导出三支概念格下的生成规则中de→g、abc→h、abcef→hk均为冗余规则。

进一步分析原因，主要是因为基于对象导出三支概念格的规则提取时考虑的是对象特性，而基于属性导出三支概念格的规则提取时考虑的是属性特性。因此单纯基于对象导出或属性导出三支概念格进行规则提取时，就会生成一些冗余规则。

为进一步消除对象导出三支概念格或属性导出三支概念格下生成的冗余规则，以下通过对象导出三支概念格与属性导出三支概念格的合并，使得在进行规则提取时受双重特性(对象特性和属性特性)约束，从而进一步减少冗余规则的生成。为此，先给出对象/属性导出合并三支概念格的定义。

定义 17 (G,M,I,N,J)是形式背景，若((X,Y),A)∈AEL(G,M,I)，(X,(A,B))或(Y,(B,A)) ∈OEL(G,M,I)，则((X,Y),(A,B))称为对象/属性导出合并三支概念，简称OAE-概念，这里(X,Y)≥=A且A≤=(X,Y)，X≤=(A,B)且(A,B)≥=X ； 或 (X,Y)≥=A 且 A≤=(X,Y)， Y≤=(B,A)且(B,A)≥=Y。其中X、Y⊆ G，A、B⊆M。(X,Y)和(A,B)称为OAE-概念的外延和内涵。

对于((X,Y),(A,B))，((Z,W),(C,D))，定义其偏序关系 ((X,Y),(A,B)) ≤ ((Z,W),(C,D))⇔(X,Y)⊆(Z,W)⇔(C,D)⊆(A,B)，形式背景(G,M,I)的所有OAE-概念在上面定义的偏序关系下是完备格，称为对象/属性导出合并三支概念格，记为OAEL(G,M,I)。

例9：合并图1的OEL(G,M,I)和图5的AEL(G,M,I)，以及图2的OEL(G,N,J)和图6的AEL(G,N,J)，所得对象/属性导出合并三支概念格OAEL(G,M,I)和OAEL(G,N,J)如图7、图8所示。

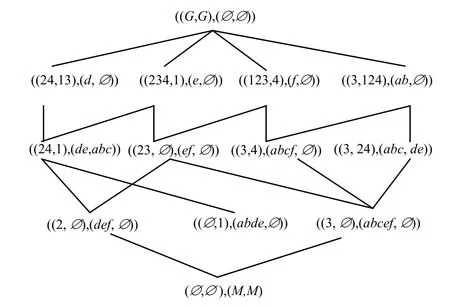
图7 对象/属性导出合并三支概念格OAEL(G,M,I)

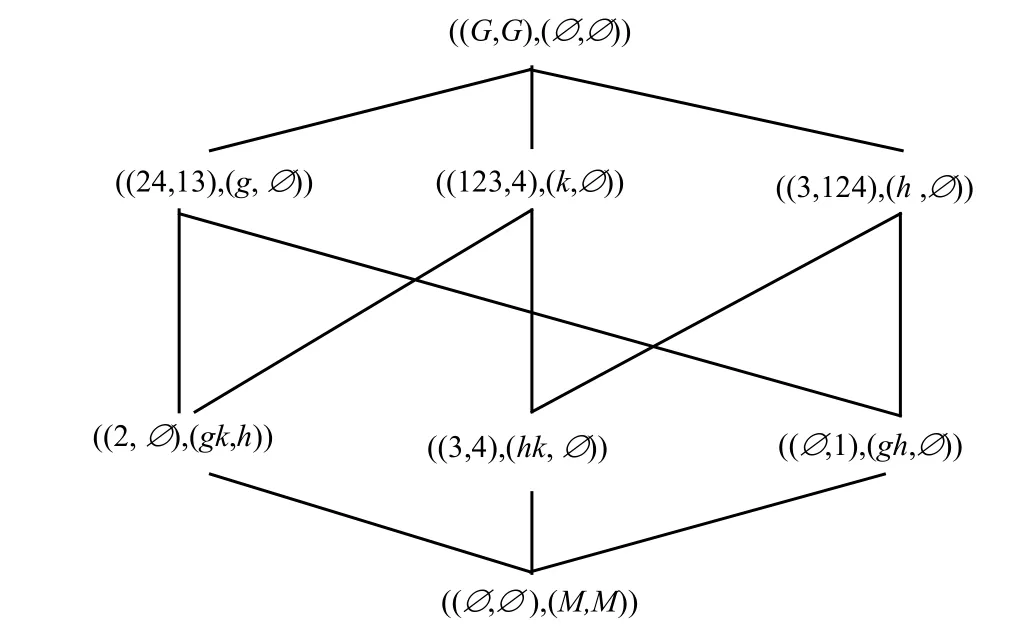
图8 对象/属性导出合并三支概念格OAEL(G,N,J)

接下来，定义对象/属性导出合并三支概念格之间的细于关系，以及决策背景基于对象/属性导出合并三支概念格的协调性。

定义 18 设OAEL(G,M,I)与OAEL(G,N,J)是对象/属性导出合并三支概念格,若对于任意((Z,W),(C,D))∈OAEL(G,N,J)，存在((X,Y),(A,B))∈OAEL(G,M,I)，使得X=Z且Y=W，则称OAEL(G,M,I)细于OAEL(G,N,J)，记作OAEL(G,M,I)≤OAEL(G,N,J)，并称决策背景(G,M,I,N,J)是基于对象/属性导出合并三支概念格协调的。

例10：表1所示决策背景的对象/属性导出合并三支概念格OAEL(G,M,I)≤OAEL(G,N,J)，所以该决策背景是基于对象/属性导出合并三支概念格协调的。

在上述定义的基础上，进一步定义对象/属性导出合并三支概念格下的生成规则。

定义 19 设决策背景(G,M,I,N,J)是基于对象/属性导出合并三支概念格协调的，若对于(X,Y)、(Z,W)≠(∅,∅)、(G,G)，有((X,Y),(A,B))∈OAEL(G,M,I),((Z,W),(C,D))∈OAEL(G,N,J)且X=Z、Y=W，则称A→C，B→D分别是一个规则。

例11：由图7、图8可以看出，因为((∅,1),(gh,∅))∈OAEL(G,N,J)，((∅,1),(abde,∅))∈OAEL(G,M,I)，根据定义19，可得规则abde→gh, ∅→∅(舍去)。

以下给出基于对象/属性导出合并三支概念格的规则提取算法。

算法1 基于合并三支概念格的规则提取算法

输入：决策形式背景(G,M,I,N,J)；

输出：决策规则集合C；

1) C=∅；

2) 构建对象导出三支概念格OEL(G,M,I)和OEL(G,N,J)；

3) 构建属性导出三支概念格AEL(G,M,I)和AEL(G,N,J)；

4) 合并OEL(G,M,I)和AEL(G,M,I)，构建对象/属性导出合并三支概念格OAEL(G,M,I)；

① 对于AEL(G,M,I) 中每个概念((X,Y),A))，若OEL(G,M,I)中存在对应概念(X,(A,B))或(Y,(B,A))，则生成新概念((X,Y), (A,B))；

② 由所有概念((X,Y), (A,B))生成对象/属性导出合并三支概念格OAEL(G,M,I)；

5) 合并OEL(G,N,J)和AEL(G,N,J)，构建对象/属性导出合并三支概念格OAEL(G,N,J)：

① 对于AEL(G,N,J)中每个概念((X,Y),A))，若OEL(G,N,J)中存在对应概念(X,(A,B))或(Y,(B,A))，则生成新概念((X,Y), (A,B))；

② 由所有概念((X,Y), (A,B))生成对象/属性导出合并三支概念格OAEL(G,N,J)；

6) 对于OAEL(G,N,J)中每个概念((X,Y), (C,D))，重复下列操作：

若OAEL(G,M,I)中存在对应概念((X,Y),(A,B))，则C = C∪{A→C，B→D}；

7) 舍去C中所有前提或结论为φ的规则，输出C。

该算法综合利用了对象导出三支概念格所包含的对象信息和属性导出三支概念格所包含的属性信息，这是因为OE概念(X,(A,B))刻画了对象子集X共同具有的属性子集A和共同不具有的属性子集B，而AE概念((X,Y),A)刻画了共同具有属性子集A的对象子集X 和共同不具有属性子集A的对象子集Y，因此相对于单纯的对象导出三支概念格或属性导出三支概念格，所得的对象/属性导出合并三支概念格同时包含了对象和属性信息，进而也使得所生成的规则在冗余性方面得到一定程度的降低。

另外，该算法的实现效率主要取决于对象导出三支概念格和属性导出三支概念格中的三支概念构建算法。关于三支概念的构建，文献[19]通过对形式背景及其补背景的变换和并置，提出一种基于二支算子的三支概念构建算法。文献[20]针对三支概念分析理论中三支概念数量庞大、构建耗时的问题，提出一种三支概念的并行构建算法。考虑到本文示例中的形式背景比较简单，因此借鉴的是一般形式概念的构建方法，在后续研究中将结合具体的应用，尝试采用上述两类新的三支概念构建算法。

例12：应用上述算法，由图7、图8的对象/属性导出合并三支概念格OAEL(G,M,I)和OAEL(G,N,J)所得的生成规则集合如下：

d→g；ab→h；f→k；def→gk；abde→gh；abcf→hk

比较前面的属性导出三支概念格下的生成规则集合：

d→g；de→g；ab→h；abe→h；abc→h；abcf→h；abcef→h；f→k；def→gk；abde→gh；

abcf→hk；abcef→hk

以及对象导出三支概念格下的生成规则集合：

d→g；de→g；ab→h；abc→h；f→k；def→gk；abde→gh；abcf→hk；abcef→hk

可以看出，对属性导出三支概念格和对象导出三支概念格进行合并以后，进一步消除了原来的冗余规则。

4 结 束 语

在决策背景的规则提取方面，现有文献基于属性导出三支概念格进行规则提取，并取得了较好的效果。本文在其基础上进一步研究了基于对象导出三支概念格的规则提取，并与经典概念格及属性导出三支概念格下的规则提取进行了比较；同时通过对象导出三支概念格和属性导出三支概念格的合并，定义了对象/属性导出合并三支概念格，并提出了基于对象/属性导出合并三支概念格的规则提取算法。理论分析和实例结果也表明了本文工作的有效性。下一步将本文提出的决策规则提取算法应用到地理课程自动解题研究，以自动获取用于地理试题解答的隐式解题规则。