图象法解一类“叠加体”模型

贵州 陈卫国

高中物理中有一类常见且重要的“叠加体”问题，用常规物理解法计算量很大，且容易出错。现试用图象法分析解答，以得到一种直观、简便的解题方法。

一、“叠加体”模型

A、B两物体的质量分别为mA和mB，A物体可视为质点，B物体长为l。两物体在水平地面上静止且A叠放在B上。A、B间的动摩擦因数为μAB，B与地面间的动摩擦因数为μB。最大静摩擦力等于滑动摩擦力，重力加速度为g。对A或B施加水平拉力F，A、B物体可能出现由静止过渡到同步加速到异步加速，直至二物体发生分离。

二、“叠加体”模型的两种典型情况

模型一F作用在A上，A在B的左端，如图1

判断“叠加体”物体能否发生相对运动(错位)的方法

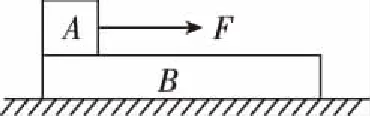
图1

1.共同加速度a0：“叠加体”类物体在外力作用下相对静止且同步前进的加速度

A、B水平受力分析如图2

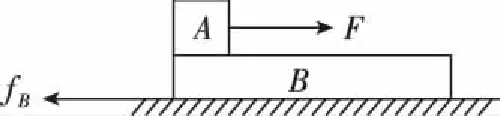
图2

2.临界加速度a1：“叠加体”类物体彼此有相对运动(错位)，水平无拉力物体仅在滑动摩擦力作用下前进的加速度

A、B水平受力分析如图3、图4

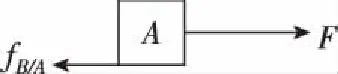
图3

图4

3.“叠加体”类物理问题，一旦它们初始条件确定，其运动情况是确定的。我们只需比较“共同加速度a0”和“临界加速度a1”即可确定“叠加体”物体是否相对运动(错位)。

如果a0≤a1，“叠加体”中两个物体将相对静止，整体共同静止或前进。

如果a0>a1，“叠加体”中两个物体将相对运动(错位)，各自加速前进。但施加F的物体加速度较大。持续下去，A将从B的右端冲出。

模型二F作用在B上，A在B的右端，如图5

判断“叠加体”物体能否发生相对运动(错位)的方法

图5

1.共同加速度a0：“叠加体”类物体在外力作用下彼此相对静止且同步前进的加速度

A、B水平受力分析如图6

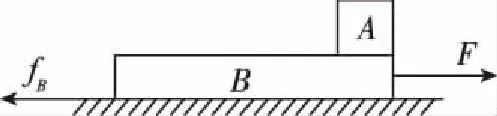
图6

2.临界加速度a1：“叠加体”类物体彼此有相对运动(错位)，水平无拉力物体仅在滑动摩擦力作用下前进的加速度

A、B水平受力分析如图7、图8

图7

图8

3.“叠加体”类物理问题，一旦它们的初始条件确定，其运动情况是确定的。我们只须比较“共同加速度a0”和“临界加速度a1”即可确定“叠加体”物体是否相对运动(错位)。

如果a0≤a1，“叠加体”中两个物体将相对静止，整体共同静止或前进。

如果a0>a1，“叠加体”中两个物体将相对运动(错位)，各自加速前进。但施加F的物体加速度较大。持续下去，A将从B的左端冲出。

【总结】对于上述“叠加体”物理模型，必须先由所给参数根据“共同加速度a0”与“临界加速度a1”关系判断A、B物体是否有相对运动。如果A、B相对静止，则整体分析；如果A、B有相对运动，须隔离A、B物体，进而分析A、B运动情况。

三、图象法解“叠加体”物理模型

1.在模型一中，“叠加体”所给参数确定，F由0逐渐增大的过程中，A、B物体将由对地静止逐渐过渡到同步加速，最后两物体将发生相对运动(错位)。在上述过程中，A、B物体发生错位时的F临界值必须满足a0=a1，即

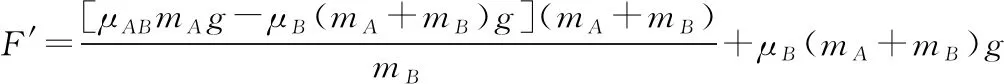
F≤F′时，A、B将相对静止

F>F′时，A、B将相对运动

(1)A、B一直对地静止，F满足0≤F≤μB(mA+mB)g

(2)A、B共同前进，但未发生相对运动，共同加速度

(3)A、B发生相对运动后，各自加速度分别为

(4)如F确定，A、B发生相对运动到二者分离，相对加速度Δa=aA-aB

发生相对运动至二者分离有

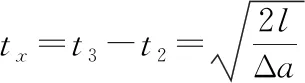
(5)“叠加体”A、B全程运动如图9

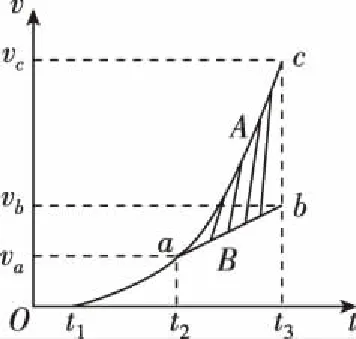
图9

其中，叠加体A、B在t1时刻同步开始加速；在t2时刻二者将发生相对运动(错位)；在t3时刻二者将分离。

二者相对运动时，B做匀加速直线运动如图直线ab，且ab直线是t1至t2段曲线在t2时刻的切线。图中阴影面积为B物体长度，即Sabc=l。

上述过程中产生的热量为

Q=fB/A·Sabc=μABmAg·l，最终A由B的右端滑出。

2.在模型二中，“叠加体”所给参数确定，F由0逐渐增大的过程中，A、B物体将由对地静止逐渐过渡到同步加速，最后两物体将发生相对运动(错位)。在上述过程中，A、B物体发生错位时的F临界值必须满足a0=a1，即

得F″=μAB(mA+mB)g+μB(mA+mB)g

F≤F″时，A、B将相对静止

F>F″时，A、B将相对运动

(1)A、B一直对地静止，F满足条件为0≤F≤μB(mA+mB)g。

(2)A、B共同前进，但未发生相对运动，共同加速度

(3)A、B发生相对运动后，各自加速度分别为

(4)如F确定，A、B发生相对运动到二者分离，相对加速度为Δa=aB-aA

发生相对运动至二者分离有

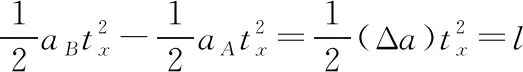
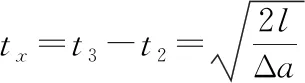
(5)“叠加体”A、B全程运动如图10

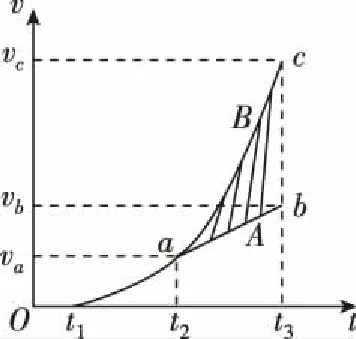
图10

其中，叠加体A、B在t1时刻同步开始加速；在t2时刻二者将发生相对运动(错位)；在t3时刻二者将分离。

二者相对运动时，A做匀加速直线运动如图直线ab，且ab直线是t1至t2段曲线在t2时刻的切线。图中阴影面积为B物体长度，即Sabc=l。

上述过程中产生的热量为

Q=fB/A·Sabc=μABmAg·l，最终A由B的左端滑出。

综合上述1和2的两种情况，我们有叠加体系统临界问题的求解思路：

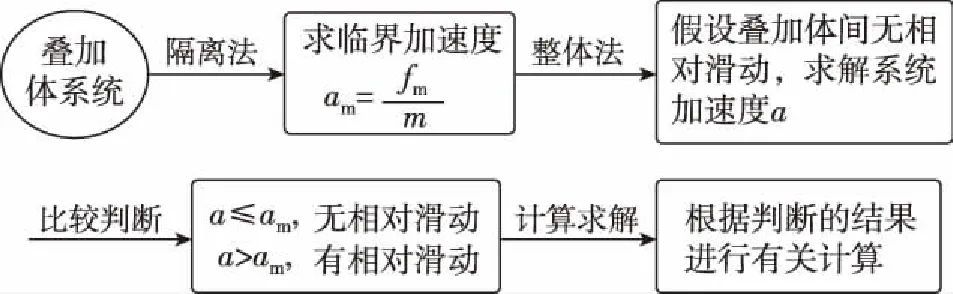
四、“叠加体”物理模型延伸拓展

1.在模型一中，F作用在A上，A在B的左端，如图11

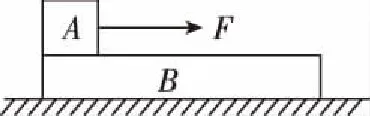
图11

(1)如果mA→∞，正常情况下，F<μB(mA+mB)g，系统将全程静止，“叠加体”问题转化为“单体”问题。

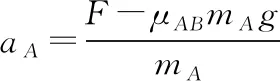
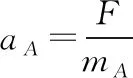
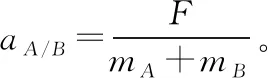
在A、B发生相对运动时，各自加速度分别为

在A、B将发生相对运动(错位)时，临界F满足

2.在模型二中，F作用在B上，A在B的右端，如图12

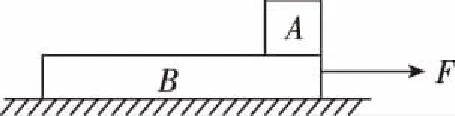
图12

(1)如果mA→∞，正常情况下，F<μB(mA+mB)g，系统将全程静止，“叠加体”问题转化为“单体”问题。

(2)如果mB→∞，正常情况下，F<μB(mA+mB)g，系统将全程静止，“叠加体”问题转化为“单体”问题。

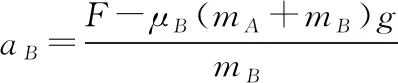
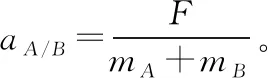
在A、B发生相对运动时，各自加速度分别为

在A、B将发生相对运动(错位)时，临界F满足

得F′=μAB(mA+mB)g

五、可化为“叠加体”物理模型的问题

【例题】一小圆盘静止在桌布上，位于一方桌的水平桌面的中央。桌布的一边与桌的AB边重合，如图13所示，已知盘与桌布间的动摩擦因数为μ1，盘与桌面间的动摩擦因数为μ2。现突然以恒定加速度a将桌布抽离桌面，加速度方向是水平的且垂直于AB边。若圆盘最后未从桌面掉下，则加速度a满足的条件是什么？(以g表示重力加速度)

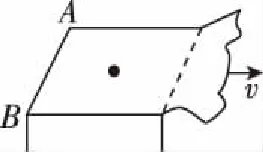
图13

解法一：公式法

令圆盘质量m，桌长l，桌布从圆盘下抽出过程中，盘以加速度a1匀加速运动，有

μ1mg=ma1

①

桌布抽出后，盘在桌面上以a2匀减速运动，有

μ2mg=ma2

②

令盘刚离开桌布时的速度为v1，盘在桌布上相对运动耗时t1，移动的距离为x1，盘离开桌布后在桌面上再运动距离x2后停下，盘在桌面上相对运动耗时t2，有

③

盘没有从桌面上掉下的临界条件是

④

桌布从盘下抽出匀加速运动加速度为a，令盘、桌布分离时桌布速度v2，在这段时间内桌布移动距离x，有

⑤

解法二：图象法

分析题意有在桌布以加速度a匀加速前进；盘先在桌布上以加速度a1匀加速前进，后脱离桌布以加速度a2在桌面上匀减速前进，临界条件为盘到桌面边缘时，速度恰为0，有

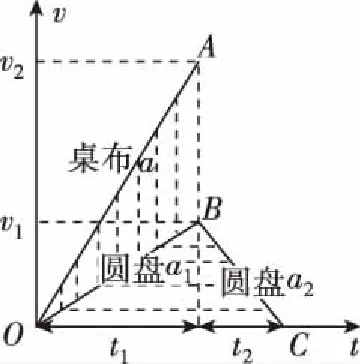
图14

如图14，令圆盘质量m，桌长l，桌布从圆盘下抽出过程中，盘以加速度a1匀加速运动，有

μ1mg=ma1

得a1=μ1g

桌布抽出后，盘在桌面上以a2匀减速运动，有

μ2mg=ma2

得a2=μ2g

在圆盘恰从桌布滑出时，圆盘相对桌布位移为

在圆盘由开始恰好到桌面边缘过程中，圆盘相对桌面位移为

对于圆盘运动分析，有

v1=a1t1=a2t2

①

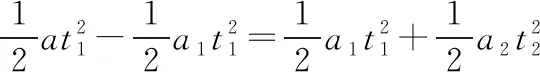
②

( )

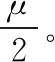
图15

A．当

F

<2

μmg

时，

A

、

B

都相对地面静止

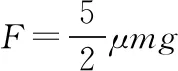
C．当F>3μmg时，A相对B滑动

【答案】BCD