地铁列车振动荷载作用下隧道底部土层孔隙水压力及变形特性研究
徐 阳, 徐佳琳, 戴 金, 许成顺, 崔春义, 孟 坤
(1. 北京市轨道交通建设管理有限公司, 北京 100068; 2. 北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124; 3. 大连海事大学土木工程系, 辽宁 大连 116026)
0 引言
随着我国城市化进程的不断加快,以城市地铁为代表的地下轨道交通得到了迅猛的发展。截至2017年12月,中国已开通地铁的城市有35个,里程共约8 000 km。地铁列车在运行过程中会产生长期的振动荷载,可能造成隧道周围土层软化、孔隙水压力增大,甚至引起土体液化。国内已出现多例地铁列车振动引起地基周围软弱地层结构破坏的情况,例如: 广州地铁1号线和2号线、天津地铁1号线和南京地铁1号线,均由于设计时对地铁列车振动引起的区间隧道振陷估计不足,没有采取适当的防治措施,在试运营阶段出现了翻浆、冒水现象[1]。
针对这一问题,国内许多学者做了大量的研究工作。唐益群等[2-4]以上海地铁为例,研究了地铁列车运行时产生的动荷载对周围土体的影响。孟光等[5]利用ABAQUS有限元软件模拟地铁运行荷载,对比分析了隧道周围土体在竖向和水平方向上距隧道不同距离处土体的变形。戴林发宝等[6]以广深港高速铁路狮子洋盾构隧道为背景,考虑流固耦合作用,通过FLAC3D 软件对列车荷载引起的地层动力响应进行了数值模拟,分析了列车高速通过隧道时孔隙水压力和超孔隙水压力比的变化规律。宫全美等[7]利用室内试验建立了地铁列车荷载作用下的孔隙水压力累积模型,并利用有效应力的有限单元法分析了列车荷载作用引起的地基液化区、轨道的变形量以及轨面不平顺值对地基液化特性的影响。
目前关于地铁振动荷载响应的研究方法主要有数值模拟和试验研究,但数值模拟与模型试验相结合的研究比较少。对于列车荷载作用下隧道周围土体的动力响应,目前已取得大量的研究成果,但由于问题的复杂性和特定工程的特殊性,所得规律难以完全适用于所有工况,且目前多数研究主要针对粉质黏土、淤泥质黏土地层的变形情况,对粉砂土层孔隙水压力的变化尚需进一步研究。正在修建中的北京地铁7号线2期(东延)沿线隧道底部土体主要为细砂、粉砂和粉质黏土层,在列车交变荷载长期作用下,局部地段存在轻微—中等的液化趋势。本文以北京地铁7号线东延线工程为背景,首先利用ADINA数值模拟典型隧道区间断面的列车荷载动力响应,然后对现场土样进行循环三轴试验,数值模拟结果和试验结果相互验证,获得隧道底部土层在地铁行车荷载作用下的孔隙水压力及竖向变形的变化规律,进而对地铁列车运行的安全性进行评价,以期研究结果为地铁工程的设计提供参考。
1 地铁隧道振动荷载数值模拟
1.1 计算模型
北京地铁7号线2期东延线敷设于朝阳、通州2个城区,是横穿北京南城东西向的重要骨干线路。从焦化厂站至终点环球影城站线路全长16.6 km,分为8个行车区间。沿线隧道底部土体主要为细砂、粉砂和粉质黏土层,潜水位埋深10.5~16.4 m。隧道埋深9.1 m,左右两隧道中心间距为16.9 m。
基于有限元数值计算平台ADINA进行建模。列车运行引起的振动属于空间作用,但由于隧道沿线纵向可看成无限延伸的等截面结构,隧道衬砌与周围土体体系承受列车动荷载作用的受力状态可以简化为平面应变的动力问题,故土体及隧道均采用平面应变四边形单元模拟。垂直于隧道延伸方向的横断面上,水平方向上长度取80 m、竖直方向上长度取35 m(大于5D,D为隧道直径)进行分析。模型顶面为自由边界,底面为全约束,设置模型顶部排水而底部不排水的单面排水方式,竖直方向自由排水。为避免波在边界面处反射,两侧采用Deeks等[8]在黏性边界基础上提出的黏弹性边界。因所建模型符合正对称条件,因此,取模型的一半进行数值分析。
采用Mohr-Coulomb模型NewMark-β法研究地铁荷载作用下隧道土体的动力响应。定义土体为Rayleigh阻尼,利用根据模态求得的固有频率进行计算,将混凝土衬砌视为线弹性材料。计算过程中各土层的参数依据勘察资料设置(见表1),各土层的泊松比均取0.3;混凝土衬砌弹性模量为3.6×1010Pa,泊松比为0.2,密度为2 500 kg/m3。为确保计算精度,对隧道周围土体网格进行加密。建立的典型断面有限元模型如图1所示。隧道周围网格划分如图2所示。

表1 典型断面处土层参数Table 1 Soil parameters of typical cross-section

图1隧道典型断面有限元模型
Fig. 1 Finite element model of typical tunnel cross-section

图2 隧道周围网格划分Fig. 2 Mesh division around tunnel
1.2 列车荷载模拟
依据列车-轨道耦合系统动力分析模型进行模拟分析。采用王明飞[1]提出的方法,考虑振动荷载经过时道床衰减,按照假定的轮轨运动关系建立列车-轨道-隧道结构系统。列车行驶上限速度取80 km/h,通过模拟分析,可以得到作用于道床底部的列车荷载激励力曲线及其功率谱,将其作为地铁列车激励荷载。得到的振动荷载时程曲线如图3所示。列车激励曲线以2点激励的形式分别作用在左右隧道的底板处,2点间距离采用我国地铁铁轨的标准轨距1 435 mm。

图3 地铁列车振动荷载时程曲线Fig. 3 Time-history curve of vibration load of metro train
1.3 数值计算结果
1.3.1 最大振动加速度
王常晶等[9]建立了列车运动荷载在地基中引起的动应力计算模型和理论,研究发现,当列车经过时,地基土受到以压应力为主的循环应力作用。张曦等[10]通过对上海地铁2号线隧道周围饱和软黏土进行现场持续的动态监测,得出垂直地铁隧道轴线水平方向土体的动力响应随距离的衰减关系式,认为随着土体深度的增大,土的剪切模量和阻尼增大,使得动荷载在传播过程中迅速衰减,直至消失。因此,本文主要考虑土层竖向应力的影响。
在距离隧道底部深度1.4、4.7、8.4、11.4、14.9 m处分别选取5条特征线,每条特征线上取10个特征点,特征点与隧道中心线的距离见图4。通过分析单次列车荷载作用下土层竖向加速度值在隧道下方土层中的变化规律,可得特征线处的最大竖向加速度和振级,如图5所示。
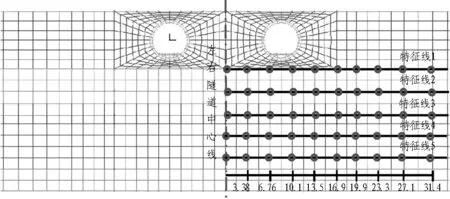
图4 加速度分析特征线示意图(单位: m)Fig. 4 Characteristic line diagram for acceleration analysis (unit: m)

图5 特征线处最大竖向加速度和振级
Fig. 5 Maximum vertical acceleration and vibration magnitude at characteristic line
由图5可知: 竖向加速度最大值出现在最靠近隧道中心线的特征点上;随着距隧道中心线距离的增大,竖向加速度短暂衰减后迅速增大,在隧道洞室截面中线附近达到最大值,之后衰减并趋于稳定;在距隧道中心线同一距离处,竖向最大加速度值随埋深的增加而减小。
1.3.2 饱和土孔隙水压力
取左隧道下方特征点1、2、3,左隧道外侧特征点4、5、6,以及左右隧道中间位置特征点7、8、9(特征点示意图如图6所示),对其在单次列车交变荷载作用下孔隙水压力的发展情况进行分析,得到特征点处孔隙水压力的时程曲线,如图7—9所示。

图6 孔隙水压力特征点示意图
Fig. 6 Diagram of characteristic points for pore water pressure analysis

图7 特征点1、2、3处的孔隙水压力时程曲线
Fig. 7 Time history curves of pore water pressure at characteristic points 1, 2 and 3
由图7—9可知: 孔隙水压力时程变化曲线呈现小幅振荡形式;在左右隧道中心线及隧道底部,孔隙水压力时程变化幅值相对较大,而在左隧道外侧,孔隙水压力变化较小;随隧道埋深的增加,孔隙水压力时程变化幅度逐渐减小。

图8特征点4、5、6处的孔隙水压力时程曲线
Fig. 8 Time history curves of pore water pressure at characteristic points 4, 5 and 6

图9 特征点7、8、9处的孔隙水压力时程曲线
Fig. 9 Time history curves of pore water pressure at characteristic points 7, 8 and 9
1.3.3 残余超孔隙水压力比分析
为研究列车通过后土体残余超孔隙水压力的情况,利用有限元软件生成单次列车过后残余超孔隙水压力比(定义为残余超孔隙水压力与初始固结压力的比值)云图(如图10所示)。由图10可知,残余超孔隙水压力比最大值出现在隧道底部,且随着土体与隧道底部距离的增加,残余超孔隙水压力比逐渐减小直至趋于0。单次列车过后,残余超孔隙水压力比随时间的消散情况如图11所示。由图11可知,最大残余超孔隙水压力比为0.067,20 min后几乎消散完毕。取20 min时间区间计算(假定列车通过周期为2.5 min/次,20 min内共8车次),则典型截面单日内行车期间隧道下卧砂土层最大累计残余超孔隙水压力比为0.147。
1.3.4 地铁列车振动荷载作用下累积孔压消散引起的隧道长期沉降分析
北京地铁7号线的首末班车时间分别为5点30分和23点15分,运营时间为1 065 min。车辆模型由一个8节编组的车辆系列组成,假定列车通过周期为2.5 min/次,则单日振动约为3 834次(振动1次的定义按照室内三轴试验的定义),每月振动约11.5万次,每年振动约138万次,10年振动约1 380万次。模型可模拟隧道运营10年后的累积孔压。

图10 残余超孔隙水压力比云图

图11 残余超孔隙水压力比随时间的消散情况
Fig. 11 Dissipation of residual excess pore water pressure with time
列车振动荷载作用下累积孔压消散引起的固结沉降按式(1)[11]计算。
(1)
式中:Sv为累积孔压消散引起的固结沉降;ui为第i层土体内不排水的累积孔压;mvi为第i层土体体积压缩系数;Ui为第i层土体固结度,若计算长期累积孔压消散引起的固结沉降,可取Ui=100%;hi为第i层土体厚度。
为评析地铁列车运行的安全性,由式(1)计算可知,隧道运营10年后由累积孔压消散引起的固结沉降量约为5.4 mm。隧道运营时间与下卧土层沉降量的关系见图12。由图12可知,随着隧道运营时间的增加,地基的累积孔压消散产生的固结变形呈现出非线性增大的趋势,但总体来说列车振动荷载引起的沉降值较小。
2 室内循环三轴试验结果分析
通过循环三轴试验,验证数值模拟分析结果,并进一步研究地铁行车荷载作用下隧道底部可液化土层的累积变形特性及孔隙水压力变化情况。由数值分析结果(图10)可得,隧道底部土层残余超孔隙水压力比最大,故取此断面隧道底部粉细砂土样进行研究。

图12隧道运营时间与下卧土层沉降量的关系
Fig. 12 Relationship between tunnel operation time and settlement of underlying soil
2.1 试验仪器及试样土性参数
试验仪器采用日本的竖向-扭转双向耦合剪切仪(如图13所示),可模拟现场实际的应力路径加荷条件,施加振动循环荷载。试样为高150 mm、外径50 mm、内径30 mm的空心圆柱体。土样取自北京地铁7号线东延工程施工现场,土层埋深7.7~16.5 m,地质年代为第四纪冲洪积层,土体主要为褐黄色或黄灰色粉细砂,基本物理参数如表2所示。

表2 土样基本物理参数Table 2 Physico-mechanical properties of soil

图13 竖向-扭转双向耦合剪切仪
Fig. 13 Vertical-torsion bidirectional coupled shear apparatus
2.2 试验方案
从数值分析平台所建立的模型中,可提取得到隧道断面底部土体所受的最大竖向荷载为5 kPa。目前关于列车振动荷载引起的隧道土层动应力的研究尚不完善,因此,参照我国铁道科学研究院给出的建议公式计算路基面动应力[12]:
qdo=0.26p(1+av)。
(2)
式中:p为列车车辆的静轴重, kN,取12t=120 kN;v为列车的运行速度, km/h,最大值为80 km/h; ɑ为速度系数,考虑到地铁运行速度较慢(不超过100 km/h)、路况较差(停靠站较多,地质条件不好),ɑ取0.005。
根据式(2)可得该工况动压应力幅值为43.68 kPa,因此,取荷载幅值为40 kPa进行试验。
首先我们选取的是苏轼的《水调歌头》,在前半部分,苏轼通过“明月几时有”的千年一问,把我们引入了一个他的思想创造出来的意境。借着天上和人间的一去一来,让我们感受到人间的真实与可贵。然而,真正让这首词名垂千古的,还在后面,其中蕴含的深意和玄奇,已经达到了出神入化的程度。大家猜的没错。正是那句——
加载频率采用式(3)[13]确定:
(3)
式中:v为列车运行速度,取北京地铁最高运行速度80 km/h;l为列车车厢长度,取19 m。
根据式(3)确定本次试验加载频率约为1.0 Hz。
由1.3.4节可知,列车单日振动约为3 834次,实际试验中取5 000次。列车振动荷载引起的土体动应力可简化为正弦波,如图14所示。

图14 动应力波形Fig. 14 Wave of dynamic stress
试验所取土样埋深为16 m左右,考虑到施工过程中隧道坑洞土体的开挖卸载会引起竖向应力减小,因此,取固结比Kc=1,假设固结条件为围压200 kPa的均等固结。为进一步研究在非均等固结条件下的孔隙水压力及土体变形特性情况,取轴向固结压力为400 kPa,进行不均等固结的循环三轴试验,如图15所示。本次试验参数见表3。

(a)

(b)

表3 不均等固结的循环三轴试验参数
2.3 试验结果分析
2.3.1 循环荷载作用下土样的超孔隙水压力变化规律
不同荷载幅值下的土体超孔隙水压力比与相对应的振动次数变化关系曲线如图16所示。由图16可以看出: 在相同振动次数下,土体的累积超孔隙水压力比随着荷载幅值的增加而增大; 荷载幅值为5 kPa时,土体超孔隙水压力比增加幅度非常小,变化规律并不明显;荷载幅值为40 kPa时,土体的累积超孔隙水压力比随着振动次数的增加而增大,累积超孔隙水压力比的增长速度随着振动次数的增加而减小。由试验数据可得,当荷载幅值分别为5 kPa和40 kPa时,超孔隙水压力比最大值分别为0.005 43和0.097 6,远不足以引起土样液化,且在试验过程中注意到,振动停止后,打开排水阀,超孔隙水压力可在瞬间消散完毕,说明地铁停运期间循环荷载下产生的超孔隙水压力可充分消散,进而验证了数值分析结果的可靠性。
当荷载幅值为40 kPa时,不同固结条件下的土体超孔隙水压力比变化情况与相对应的振动次数关系曲线如图17所示。由图17可以看出,不同固结条件下的土体超孔隙水压力比有相同的增长趋势,但最终不均等固结条件下的累积超孔隙水压力比较均等固结条件下的累积超孔隙水压力比小。

图16不同荷载幅值下超孔隙水压力比与振动次数的变化关系
Fig. 16 Relationship between excess pore water pressure ratios and vibration times under different load amplitudes

图17不同固结条件下超孔隙水压力比与振动次数的变化关系
Fig. 17 Relationship between excess pore water pressure ratios and vibration times under different consolidation conditions
2.3.2 循环荷载作用下土样的累积变形分析
不同荷载幅值条件下的土体累积应变与振动次数的关系曲线如图18所示。由图18可以看出: 当荷载幅值为5 kPa时,土体未产生明显变形;当荷载幅值为40 kPa时,在前1 000次振动中变形急剧增大,约完成总变形量的80%以上,之后逐渐趋于稳定,试验过程中最大应变达到0.002 63%。

图18不同荷载幅值条件下的土体累积应变与振动次数的关系曲线
Fig. 18 Relationship between accumulated strains of soil and vibration times under different load amplitudes
当荷载幅值为40 kPa时,不同固结条件下的土体累积应变与振动次数的关系曲线如图19所示。由图19可以看出: 2种固结条件下土体累积应变的变形发展趋势大致相同;不均等固结条件下的累积应变较均等固结下的累积应变大,为0.004 91%。

图19不同固结条件下的土体累积应变与振动次数的关系曲线
Fig. 19 Relationship between accumulated strains of soil and vibration times under different consolidation conditions
3 结论与讨论
1)当列车通过隧道时,孔隙水压力增大,但增加幅度较小。超孔隙水压力比最大值出现在隧道底部,增大值随土体埋深的增加而减小。日单次行车引起的下卧砂土层瞬态残余超孔隙水压力20 min内可基本消散完毕,考虑到夜间停运期间超孔隙水压力会消散,单日行车往复荷载作用下产生的最大累积残余超孔隙水压力足以完全消散。通过循环三轴试验可知,试验振动停止后,打开排水阀,也可观察到超孔隙水压力很快消散。
2)选取数值模拟中孔隙水压力上升最大的隧道底部土层的土样进行循环振动三轴试验,发现相同振动次数下,土体的累积超孔隙水压力比和累积应变量随着荷载幅值的增加而增大;均等固结条件下的超孔隙水压力比较非均等固结条件下的超孔隙压力比大,但累积应变量小。
3)由数值模拟及室内土工试验结果表明,地铁列车振动荷载会引起隧道底部土层产生超孔隙水压力和基底沉降,但累积超孔隙水压力与应变量都较小,引起隧道底部土层液化的可能性很小。
4)列车振动荷载引起的隧道底部土体动应力场十分复杂,不但包括竖向循环正应力和循环剪应力,而且包括水平向循环正应力[14],后续试验可进一步研究列车振动荷载下竖向循环正应力与水平向循环正应力的耦合效应对隧道底部土层孔隙水压力的影响以及土体的变形特性。

