基于EEMD与极限学习机的短期风速组合预测模型
孙驷洲,陈 亮,郭兴众,陆华才,胡明星
(1.安徽工程大学 电气工程学院,安徽 芜湖 241000;2.安徽省科学技术研究院 项目管理中心,安徽 合肥 230001;3.安徽工程大学 电动汽车V2G工程技术研究中心,安徽 芜湖 241000)
风能是一种环境友好型且分布广泛的可再生能源,风能开发利用受到各国政府重视.大规模风力发电可以减少二氧化碳的排放,减缓温室效应.由于风速具有波动性和随机性大的特点,风力发电的不稳定性影响电力系统的安全可靠.如果风电场输出功率能够准确预测,电力管理部门就能依据风电功率变化规律调整电力调度、电力设备维修和保证电网的供需平衡等,所以,风电功率的预测是风电场日常管理的基本任务,也是风电研究的重要课题之一[1].按照预测时间划分,风速预测主要分为短期预测、中期预测和长期预测,其中提前一天的短期风速预测对风电场日常调度管理具有非常大的应用价值[2].
近年来,国内外研究者开发出多种不同的风速预测模型,主要分为基于风电场物理模型预测和基于历史数据时间序列预测.物理模型预测方法依据风电场的环境、地理和气象信息建立风速预测模型来预测长期风速.基于历史数据的风速预测主要分为统计方法和人工智能方法.与统计预测方法相比,人工智能预测方法更能捕捉风速数据中的非线性[3].风速人工智能预测方法有最小二乘支持向量机(LSSVM)[4-5]、BP神经网络(BPNN)[6]和极限学习机(ELM)[3,7]等.LSSVM的核函数等参数影响其风速预测效果.文献[4-5]利用LSSVM核函数将输入变量映射到高维特征空间,在高维特征空间回归训练,建立输入与输出变量之间的线性关系.文献[5]利用信号变分模态分解技术,将风速数据分解成相对稳定的模态分量,对各模态分量分别建立LSSVM风速预测模型,应用改进的差分算法对LSSVM的核参数优化选择,获得了较高的风速预测值.但当样本特征变量在高维空间中分布不平坦或存在异构信息时,LSSVM回归处理能力就受到很大的影响.
BPNN通过调整神经网络结构输入输出点、连接权值及隐含节点数,将输入节点维数欧氏空间非线性映射到输出节点维数欧氏空间,可以回归训练任何非线性函数.文献[6]将BP神经网络作为核心预测机对短期风速进行预测,获得了较高的预测精度,但BPNN容易陷入局部最优且收敛速度慢.鉴于LSSVM和BPNN的回归训练不足,采用ELM来预测短期风速.ELM具有简单、学习速度快和泛化能力强的特点,而且参数设置简单.但是ELM的输入权值和隐含节点阈值随机选择后,就直接进行回归预测,这会影响ELM风速预测精度,为此,利用全局寻优能力强引力搜索算法(GSA)[8]来优化选择ELM的输入权值和隐含层阈值,获得最优参数集后,再建立风速预测模型,增强ELM风速预测性能.为了降低风速波动性和随机性,信号经验模态分解方法(EEMD)算法将风速分解成不同频率相对稳定的子集,提高ELM预测精度.江岳春[9]利用EEMD将风电功率时间序列分解成不同的IMFn和Res,然后,把IMFn和Res作为输入变量,用LSSVM预测超短期风电功率,获得了较好预测结果.
文中将EEMD、ELM和GSA算法相结合,构建EEMD-GSA-ELM短期风速预测模型.最后用安徽某风电场的历史数据来验证该短期风速预测模型的有效性.
1 EEMD 风速分解原理
EEMD是Huang[10]在EMD基础上提出的信号经验模态分解方法,EEMD算法对原始信号添加辅助噪声来消除信号中的间歇现象后,通过“筛分”处理对信号的分解,得到相对稳定的不同尺度IMF(Intrinsic Mode Function)分量和一个剩余分量Res(Residual).EEMD对风速分解过程如下:
(1)在原始风速时间序列中添加随机高斯白噪声信号n(t),得
S(t)=s(t)+n(t),
(1)
式中,s(t)和S(t)分别为原始风速和加入随机高斯噪声信号后得到的风速时间序列.
(2)利用EMD算法将处理后的风速数据S(t)分解成各阶IMFci(t)和一个剩余分量r(t),得到
(2)
(3)经过多次重复(1)~(2)过程得到Si(t),每次加入高斯白噪声服从式(4).
(3)
(4)
式中,ε和N分别为噪声幅值和总体个数;εn为原始风速时间序列与IMF相加之和之间的误差值.
(4)根据高斯白噪声频谱的均值为零的原理,将分解得到的IMF分量累加后求均值,消除加入的高斯白噪声分量,如式(5)所示.
(5)
为了对比EEMD和EMD对信号的处理能力,EEMD和EMD对混合信号进行处理,如式(6)和图1所示.
y(t)=y1(t)+y2(t),
(6)
式中,
y1=sin(20πt),0≤t≤0.4,
(7)
(8)
EEMD和EMD对同一混合信号y(t)分解的结果如图2和图3所示.从图2中可以看出,通过EMD分解得到的不同频率的子集存在模态混叠(mode mixing)问题,而在图3中,模态混叠问题基本解决.
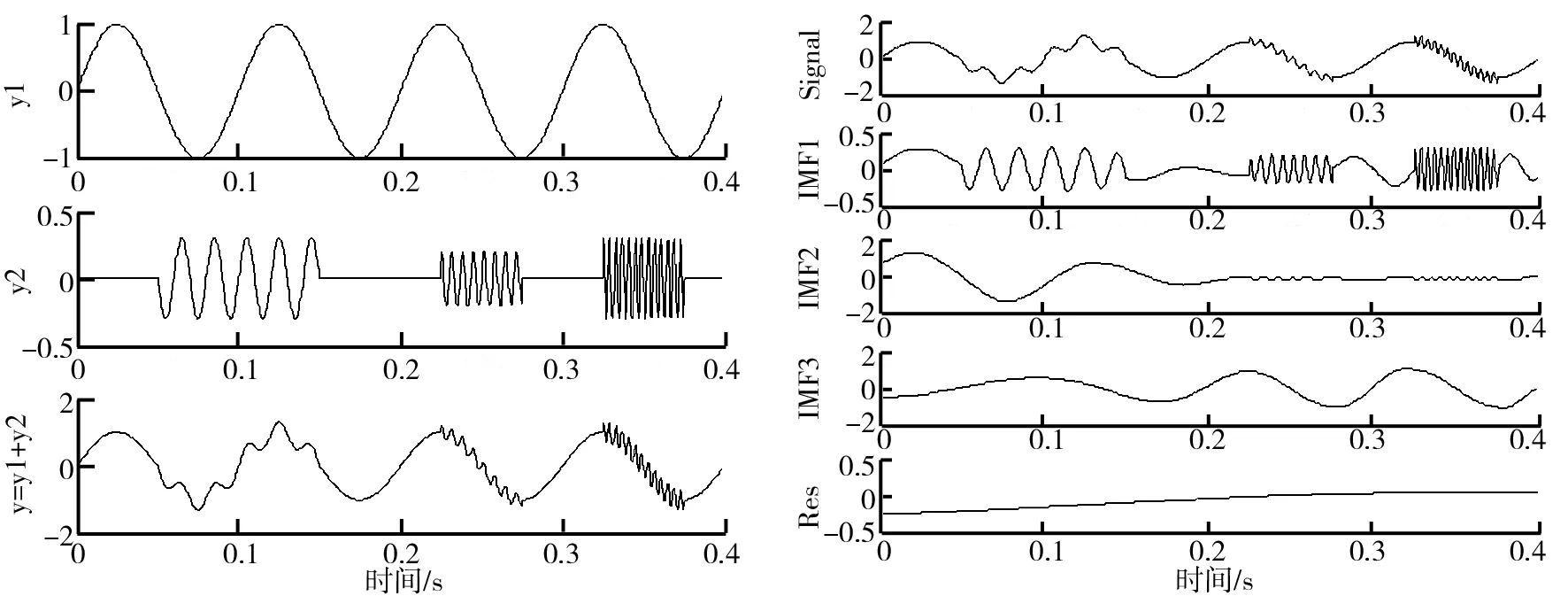
图1 混合信号 图2 EMD信号分解结果
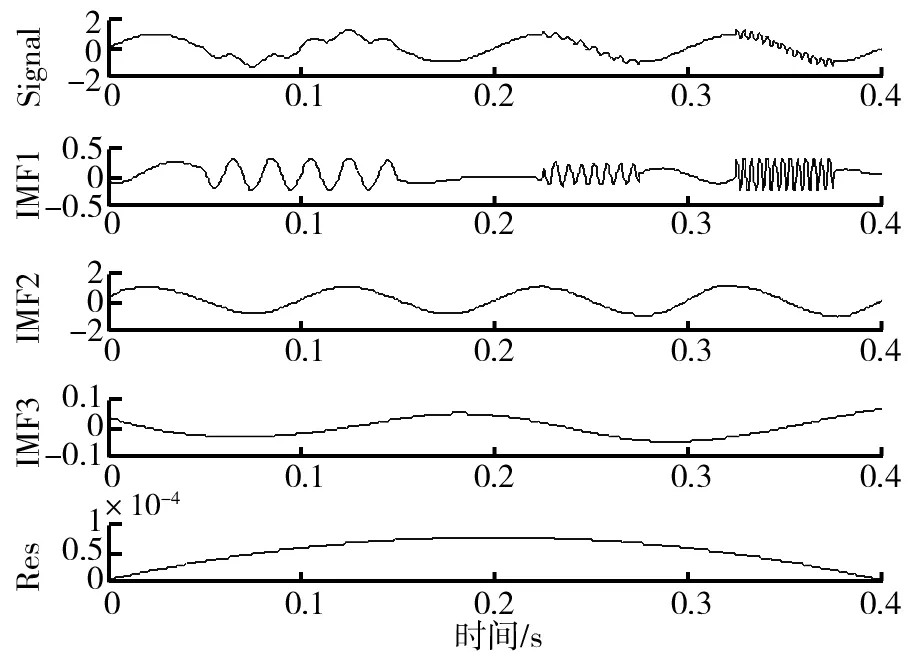
图3 EEMD信号分解结果
2 极限学习机(ELM)的基本原理
极限学习机是一种基于单隐层前馈神经网络(SLFN)的新算法,它的隐含层偏差和输出权值可以不需要调优,当输入权重和隐含层偏差随机产生后,输出权值简单地通过应用广义隐层输出矩阵的逆运算求解得到,所以,极限学习机具有调节参数少、回归学习速度非常快和泛化性能强等特点[3].
假定N个风速样本{(xi,yi)|i=1,…,N;xi=xi1,…,xin∈Rn;yi=yi1,…,yim∈Rm},SLFN网络激励函数G(x)和隐含层节点数为L,则ELM的输出如式(9)所示.
(9)
式中,ai为输入层到第i隐含层节点的权值;βi为第i隐含层节点到输出的权值;bi为第i隐含层节点的阈值;G(x)选择Sigmoid励函数,如式(10)所示.
(10)
式(9)可以简化为式(11)所示,
Hβ=T,
(11)
式中,β、H和T如式(12)所示,
(12)
H为通过激励函数计算出的ELM隐含层的输出N×L矩阵.
在ELM中,随机产生输入权值ai和隐含阈值bi,SLFN隐含层输出矩阵H就能按照式(11)和式(12)惟一确定.求解β转化成如式(13)所示求解线性系统最小二乘解.
(13)
式中,H+是输出矩阵H的Moore-Penrose广义逆.
3 重力搜索优化算法
引力搜索算法(GSA)是Rashedi等提出的一种基于万有引力定律的新型启发式优化算法[8].与常规随机搜索的优化算法PSO相比,它具有更强的全局搜索能力.GSA依据宇宙空间物体在万有引力相互作用下向质量大的个体移动的原理,利用个体质量大小衡量它的优劣来寻找最优解.在风速预测过程中,个体质量越大,则适应度值越小,个体性能越优.
Step 1:设在搜索空间中随机产生初始群体X,第i个个体的速度vi和位置xi如式(14)所示.
(14)
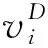
Step 2:个体质量Mi(t)依据个体的适应度值计算得到.对于风速预测而言,best(t)代表最小适应度值,而worst(t)代表最大的适应度值.
(15)
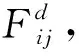
(16)
Mpi和Mpj分别为个体i和个体j的惯性质量,Mpi(t)=Mpj(t)=Mi(t);ε为非常小的常数.G(t)为通过式(17)计算t时刻的重力常数.
G(t)=G0e-αt/T,
(17)
式中,G0和α是常数,而T为最大迭代数.G0和α分别取值为100和20.
在搜索空间中,第i个个体所受到的其他个体作用力的合力,用随机加权其他个体作用力之和表示,如式(18)所示.
(18)
(19)
在t+1时刻个体i的速度和位置按式(20)更新.
(20)
式(18)和式(20)中,rand为[0,1]之间的随机变量.
4 EEMD-ELM-GSA短期风速预测模型
4.1 风速预处理
风速时间序列具有波动性大、随机性和非线性等特点,研究提出聚类经验模态分解、极限学习机和引力搜索算法相结合的风速预测组合模型.首先,利用EEMD将风速数据分解成相对平稳的不同尺度的分量IMF1~IMFn和余量Res(t);对IMF1~IMFn和Res(t)进行归一化处理,如式(21)所示.
(21)
式中,xi、xmax和xmin分别为原始数据、原始数据最大值和最小值.
4.2 适应度函数的选取
在GSA优化过程中,选用均方根误差(Root Mean Square Error,RMSE)作为适应度函数来选择ELM的输入权重和隐含层阈值参数,如式(22)所示.
(22)
式中,s(t)和s′(t)分别表示原始风速数据和训练输出值.当RMSE值越小,则ELM参数值就越优.
4.3 预测性能评价指标
用RMSE、平均绝对误差MAE(Mean Absolute Error)、平均绝对百分比误差MAPE (Mean Absolute Percent Error)统计指标评价预测结果,如式(23)和式(24)所示.
(23)
(24)
式中,s(t)和s′(t)与式(22)的功能相同.
4.4 短期风速预测模型工作过程
将各分量分别建立ELM 子预测模型,并用GSA优化算法对ELM的输入权重和隐含层阈值进行参数优化,提高ELM的回归性能;然后,将各分量的子预测模型输出值进行叠加,得到最终的短期风速预测值并进行反归一化处理.采用EEMD-ELM-GSA短期风速预测模型具体工作过程如图4所示.
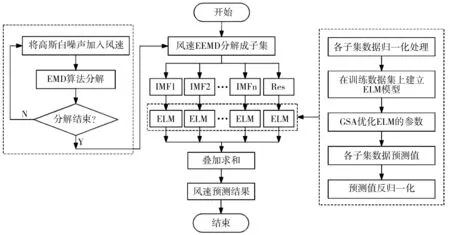
图4 EEMD-ELM-GSA短期风速预测模型
5 实例分析
5.1 研究对象
文中随机选用安徽东部某风电场2015年15 d历史风速数据对预测模型进行验证.风速数据每间隔10 min采样一次,共有2 160个数据.为了预测需要,将每小时内数据进行半小时平均处理,得到720个数据,如图5所示.前14 d 672个数据作为模型的训练样本,第15 d 48个数据作为测试样本.风速样本统计性分析如表1所示,从图5和表1可以看出,风速从0.15 m/s到13.56 m/s随机波动大且没有规律性.
5.2 预测结果分析
算法的运行环境为Window 7, Matlab 2014a, Intel(R) Core(TM)i5-4460 @3.2GHz 和8GB RAM的系统.

表1 风速数据统计
风速数据统计如图5所示.由图5可知,风速表现出非常大的波动性.为了更好地预测风速,首先,利用EEMD对风速进行分解,得到不同频率的IMF1~IMF6和一个Res,如图6所示.风速EMD分解结果如图7所示.从图7可知,EMD和EEMD分解的各分量IMF1到IMF6都是依次从高频到低频.高频分量代表风速的随机成分,而低频分量代表风速的周期性分量和长期走势.从分解的高频分量IMF1来看,EMD幅值在[-1.5,1.5]内波动,而EEMD幅值波动较小,在[-1,1]之间,这说明EEMD对风速的高频分解比EMD分解得更彻底[5].
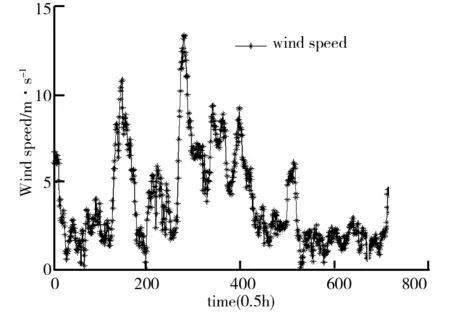
图5 风速时间序列
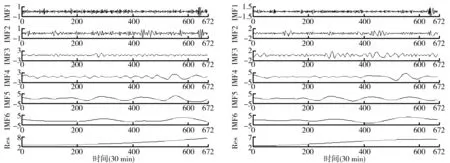
图6 EEMD分解风速数据结果 图7 EMD分解风速数据结果
为了测试所提出的风速预测模型的性能,分别利用ELM、EEMD-ELM、EMD-GSA-ELM和EEMD-GSA-ELM四种模型对短期风速进行预测,并用统计指标对其评价.GSA算法的参数设置:个体数为30,个体维数为n×(l+1)(式中n为输入变量数,l为隐含节点数).算法最大迭代次数为200,输入权值和隐含节点阈值的取值范围分别在[-1,1]和[0,1]之间.预测误差统计指标和预测曲线分别如表2和图8所示.由表2和图8可以得出,GSA优化EEMD-ELM的组合风速预测模型的RMSE为0.152 m/s,比其他ELM、EEMD-ELM和EEMD-GSA-ELM模型的预测性能更好,这说明文中提出的EEMD-GSA-ELM模型能够提高短期风速预测的精度.相对于组合模型,没有风速分解的单模型ELM预测效果最差,这表明风速分解降低了风速波动性,能降低ELM的预测难度,从而提高了ELM的预测精度.EEMD-GSA-ELM的MAPE比 EMD-GSA- ELM的MAPE低0.84%,因此EEMD比EMD对非线性风速数据分解得更好.同样可知,ELM输入权值和隐含节点阈值优化后可获得更高精度.

表2 预测结果对比
为了进一步验证该模型的优越性,利用相同风速数据,将EEMD-GSA-ELM与Persistence和WT-GA -SVM[11]预测模型相比较,其中,Persistence以当前风速值预测下一时刻风速值,且不需要历史风速值训练,它对风速单步预测具有较好的效果,往往作为校验新风速预测模型的基准模型.WT-GA -SVM模型利用小波变换WT技术将风速分解成3级高频细节信号和低频逼近信号,GA优化SVM的核函数后预测短期风速.WT-GA-SVM的参数设置参考文献[11],预测结果如图9和表3所示.通过预测统计指标来看,所提出的风速预测模型比WT-GA-SVM模型的性能更优,RMSE、MAPE和MAE的值分别提高了0.054 m/s、2.57%和0.047 m/s,这是因为EEMD具有更好的风速分解能力,ELM比SVM有更强的网络计算和泛化能力.同样,与基准模型Persistence相比,EEMD-GSA-ELM预测精度更高,RMSE、MAPE和MAE的值分别提高了0.232 m/s、11.32%和0.219 m/s.
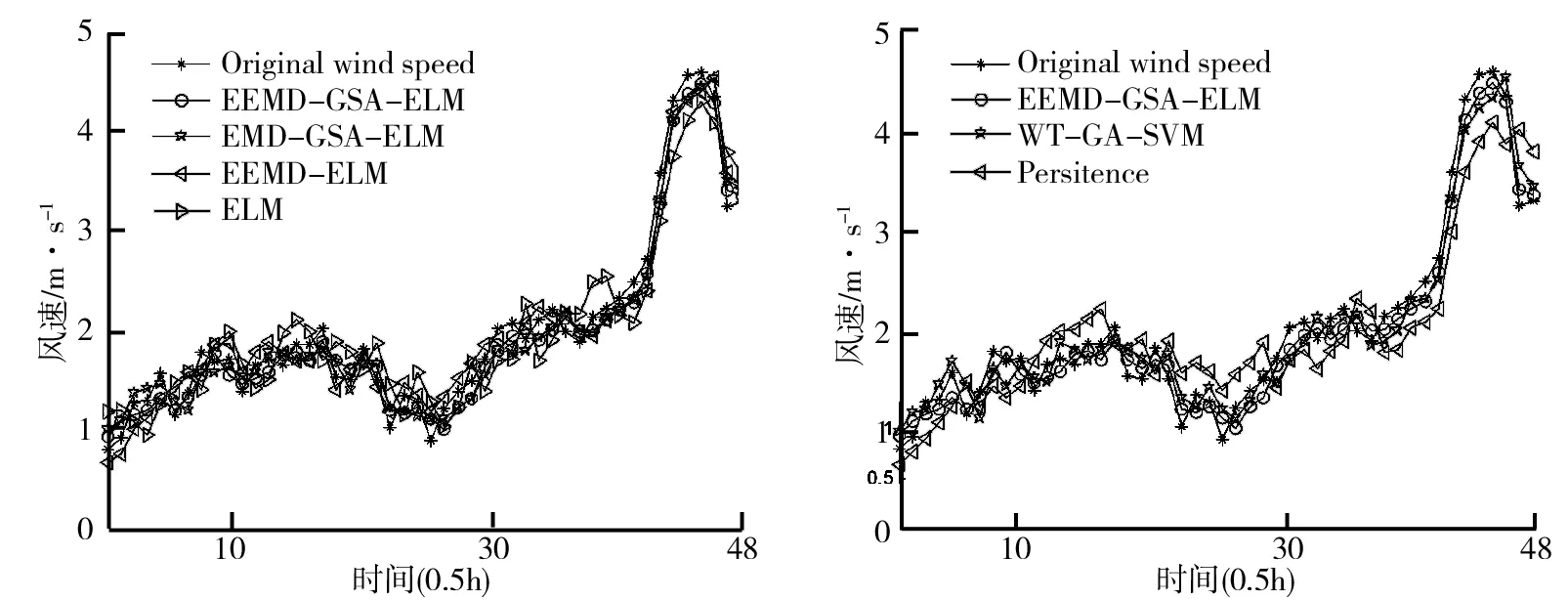
图8 不同模型风速预测结果 图9 不同模型风速预测结果

模型RMSE/m·s-1MAPE/%MAE/m·s-1Persistence0.38419.510.360WT-GA-SVM0.206010.760.188EEMD-GSA-ELM0.1528.190.141
6 结论
研究将经验模式分解算法用于风速时间序列的非平稳性处理,对分解后的各IMFn和Res建立ELM模型,GSA算法优化ELM的参数,对各子集预测结果叠加求和得到最终短期风速预测值.通过实验、分析和比较,可以得出下列结论:①EEMD 分解风速时间序列后,降低了风速数据非平稳特性,提高了风速预测精度.与 EMD 算法相比,EEMD通过添加高斯随机变量后对风速时间序列分解得更加彻底.②采用ELM模型进行短期风速预测,ELM的输入权重和隐含层阈值参数的选取影响ELM的精度.采用GSA算法对上述参数进行优化,使ELM更好地捕捉风速中的非线性分量.与EEMD-ELM、EMD-GSA-ELM和WT-GA-SVM相比,都获得了较好的预测效果.③同样,与单一预测模型ELM和Persistence相比,EEMD-GSA-ELM组合预测模型能更加有效地预测短期风速.所以,文中提出的风速预测组合模型能较好地预测风速.

