乌鲁木齐市PM2.5及其影响因素关系的研究— —基于VAR模型的脉冲响应和方差分析

（新疆财经大学应用数学学院，乌鲁木齐市，830012） 董雷萍

1 引言

大气颗粒是目前我国乃至全世界的首要对人体的健康和生存造成危害的污染物，它同时会对与大气中其他成分相互作用产生化学反应、影响人类活动的可见度、或形成酸雨、积聚而影响云的产生等。随着国家对一带一路的政策实施，作为一带一路经济带的西北重要转折站乌鲁木齐市的环境越来越受到重视，环境的发展关乎到经济的稳定和国民的健康。

传统的测量方法已不能满足对PM2.5的研究，加之PM2.5及其连带污染物又是时间序列模式，故可以考虑与金融时间序列联系起来，一来本身对金融时间序列研究的就是在时间序列范围内跟PM2.5数据的选取比较类似，另一方面，环境经济的影响以及经济与环境之间的影响理论上是相互的，虽然暂时国内还没加重这一研究趋势，但不得不承认，人类的发展必然与社会环境的生存同步，故本文尝试用金融时间领域方法对乌鲁木齐市的PM2.5及其影响因素的关系做进一步探讨。

国外学者对PM2.5研究的主要有：Houthuijs等[1]主要要就欧洲东部的PM2.5和PM10进行研究，把PM10的浓度的增加归因于PM2.5的浓度的增加；Chow等[2]通过对美国PM2.5的源解析，发现碳元素和有机碳是PM2.5的主要成分；Vega等[3]使用墨西哥2000～2002年的一些特定的数据来研究，发现在工业生产区和日常的PM2.5浓度更高；实际上，PM2.5具有时空分布的差异,Russell和Allen[4]对美国德州南部PM2.5组成物质的有机碳进行研究，结果表明其从初秋到冬末浓度值相对较高，而且在靠近城市的区域浓度值更高。Tran等[5]对阿拉斯加的费尔班克斯将近十年收集到与空气相关的数据对PM2.5和空气污染物及空气环境状况进行了研究，给出会对PM2.5浓度产生不一样影响的气象条件。

国内的于建华等[6]对北京地区PM10和PM2.5质量浓度变化特征的研究也发现PM10中小颗粒PM2.5的含量比粗粒子PM2.5-PM10的多；紧接着，朱先磊等[7]在研究北京市PM2.5来源中发现PM2.5主要来自日常生活的污染等；李军等[8]使用非参数方法探索了气象对PM2.5的影响，得到季节与PM2.5之间的相互作用；王菊等[9]运用系数和t检验对长春环境空气相关性的研究也表明PM2.5和PM10之间存在关联。Zhang等[10]和Dai等[11]则分别对青海湖地区和深圳PM2.5的情况；徐伟嘉等[12]运用地统计的描述出珠三角地区PM2.5时空自相关性和气象因素的影响；瞿德业等[13]对兰州市PM10和PM2.5污染情况进行分析，进一步也发现增加的现象。

国内外的文献追溯历史到现在主要是对PM2.5空气污染物的来源及其危害因素进行探究，而对本身与这些动态污染物之间的探究确是有限，而在实际中PM2.5的浓度变化与气温、SO2、CO、NO、NO2、O3等气象因素密切相关，尤其在未经大势开发边缘地区，基于以上考虑，使用建立VAR模型的脉冲响应分析方法，利用2015～2016年乌鲁木齐市环境监测站每日监测到平均数据对其影响因素做出了分析，一方面靠着广义脉冲响应函数法来分别研究PM2.5与其影响因素之间的动态冲击反应，来描绘PM2.5与其影响因素长期相互动态结果。另一方面是运用方差分解技术来进一步研究PM2.5与其影响因素在说明相互变动时的相对重要性。

2 计量方法

2.1 VAR模型

向量自回归（VAR）模型，是建立在向量基础上的AR模型，根本上是研究许多变量之间存在的一种动态的关系，即用当前的一切变量对它的滞后期的变量进行回归，一般不用事先设定任何限制性的条件，就能估计出互相依赖的时间序列整体系统，和任意随机扰动项对整体产生影响的动态关系；VAR方法就是构造出一个模型，模型内将每个内在的变量看作是所有内在变量的滞后值，VAR（p）为p阶向量自回归模型的数学形式:

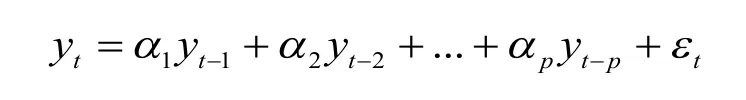
其中 εt=(ε1t,ε2t,...εnt)'为n×1维随机扰动项，服从高 斯 白 噪 声 ，即 期 望，方 差 var(εt)=σ2，为维系数矩阵的待估计的参数，是k维内在的变量，本文将选用了5个指标作为模型的内在的变量，yt-1, yt-2,...yt-p表示yt的滞后期，p为滞后阶数，VAR模型转化为矩阵为：

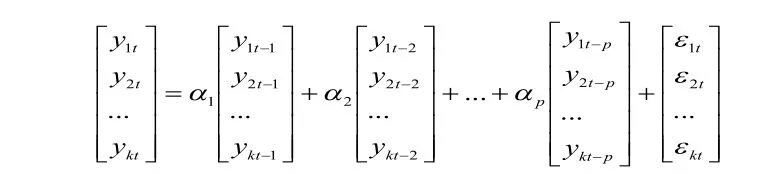
2.2 脉冲响应分析

脉冲响应函数是检验建立的模型中，每一个内在的变量对他自己和其他的内在变量变化产生的影响；变化意思是某个内在的变量收到的一定的干扰或者是冲击，即它的误差变动了；影响是说当模型的误差变动的时候影响他自己和其他内在的变量；事先假定模型是平衡的，现在要是某一个干扰项对系统产生冲击，此时系统对它做出反应偏离了原位置，接着后期又恢复均衡这就是脉冲相应函数的过程。

跟单变量自回归模型相似的是，假设VAR（P）模型为平稳的，那么肯定可以用一个平均模型MA（∞）的形式来写出。假设n阶平稳的VAR（P）模型为：

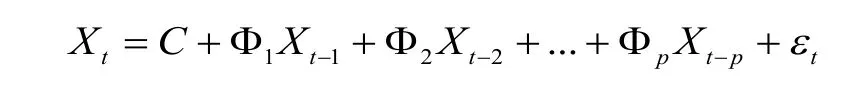
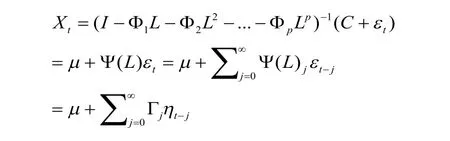
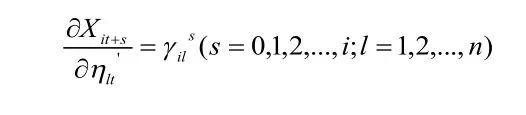
表示第i个分量Xi在t+s时刻对l个分量对应的扰动项ηt在t时刻变动一个单位（保持其他扰动项不变）的相应值，这些相应都是时间间隔s的函数，被称为脉冲相应函数，显然总共有 n2个这样的脉冲相应函数。

2.3 方差分析

跟点变量自回归模型一样的是，若对平稳的VAR（P）模型进行l步预测，那么最好的预测结果也是基于条件期望下的结果，故而得到预测的误差方差为：

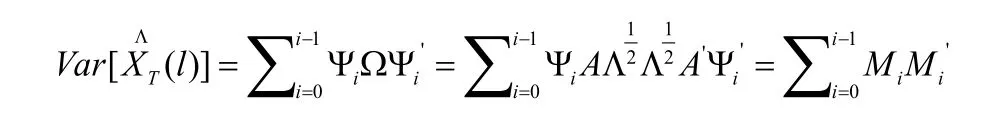
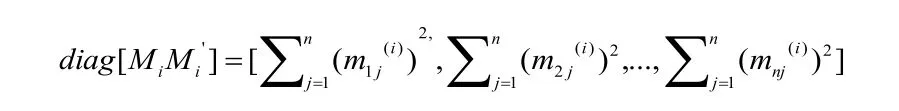
则第k个分量预测的方差为：

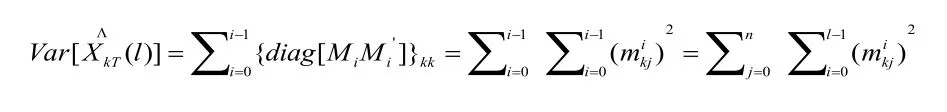
从而得到第j个分量干扰项对第k个分量预测的方差的贡献是：

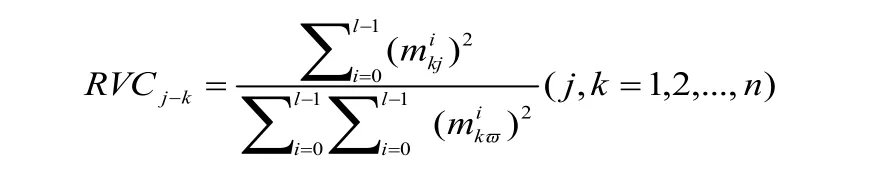
方差分解的基本思想：将系统中的全部内在的变量的波动按照它所占的成分进而分解成跟每个方程信息相联系的k个小部分，进一步得出信息对模型的内生的变量的相对重要性；也就是说在预测误差的方差中，关于对变量的原因进行了阐述，从而把模型的动态表示出来。

3 数据来源

本文的数据是2013年1月1日起乌鲁木齐市环保局通过网络向公众发布全市大气污染监测站的监测的所有空气中 6 种污染物（PM10、SO2、NO2、PM2.5、CO、O3）的每隔一个小时就更新发布的监测数据，别是监测站、收费所、新疆农科院农场、铁路局、三十一中学、七十四中学、米东环保局、培训基地，其中米东环保局是2017年新增加的一个监测点，因为PM2.5、CO和O3这3种污染物才监测没多久，因此不排除有时会出现数据的缺测误测等现象；本文截取的是从2015年1月1日到2016年12月31日这段期间内，乌市的大约723天这些污染物每天的浓度平均值。

4 实证分析

4.1 ADF（单位根）检验

由于虚假问题的存在，所以在进行有效的拟合前必须先检验各序列的平稳性，只有当各序列都平稳时，才可以大胆的使用模型的各种后续模型的处理，首先对数据进行ADF检验：

单位根检验原理：通过检验特征根周围的分布（即单位圆内还是单位圆上外），来检验序列的平稳性，本文为了减少数据的波动性，对数据进行对数化处理，结果如表1：

由表1可知在显著性分别为1%和5%的情况下，6个变量序列PM2.5PM10SO2、NO2、CO、O3总体趋于平稳的。

4.2 滞后阶数确定

在进行了单位根检验之后，进一步建立VAR模型。接下来就是确定模型的阶数p。

通常是以（AIC）和（SC）取值最小准则来确定滞后阶数，如果AIC和SC同时取不到最小，就可以用（LR）检验来确定；如果滞后阶数太大，则模型中需要估计的参数就越多，模型自由度受到一定的限制，从而模型的准确性降低。从结果上看FPE,AIC在滞后5期最好，p定为5，模型拟合效果 R2为81.20，调整后的 R2是80.88，由表可以看出向量自回归AR（5）的拟合情况是这里面最好的，检验结果后可建立VAR模型如下：

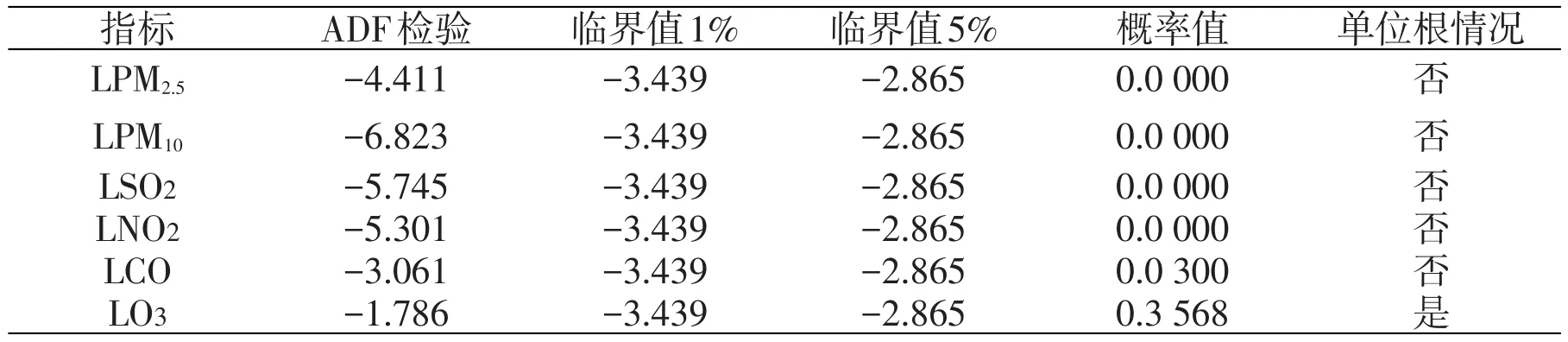
表1 单位根检验的结果

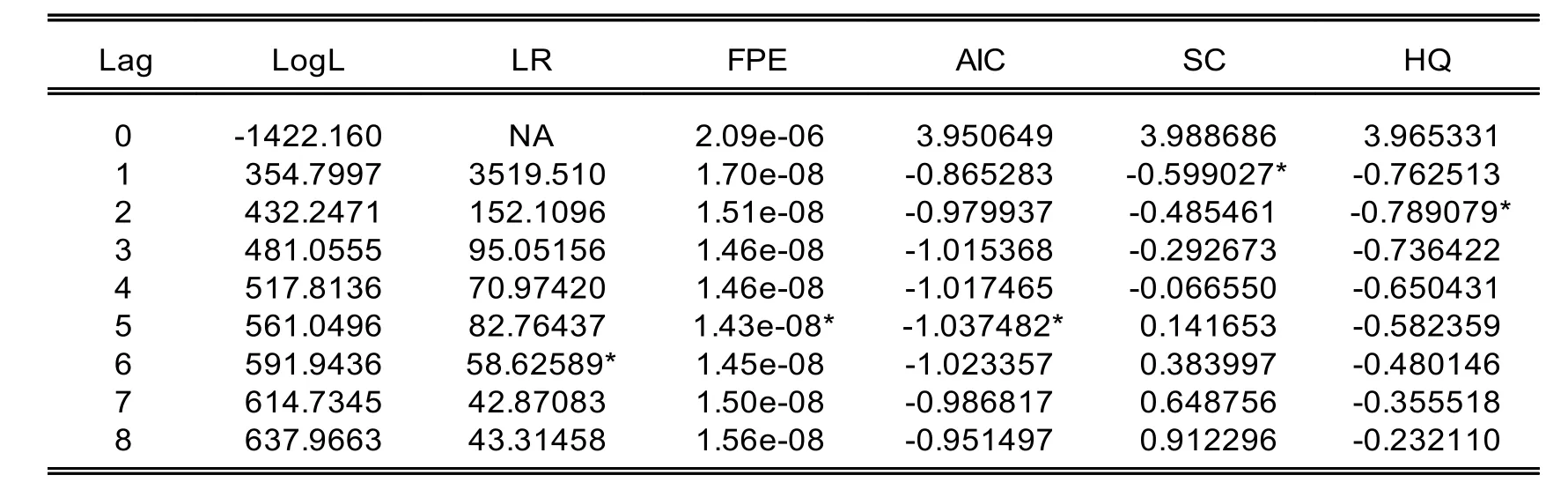
表2 滞后阶数的检验

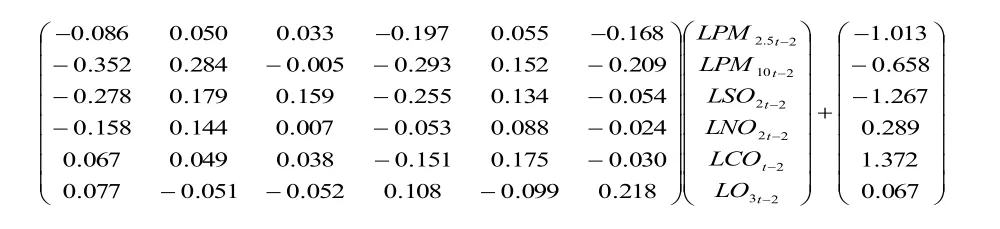
4.3 稳定性检验

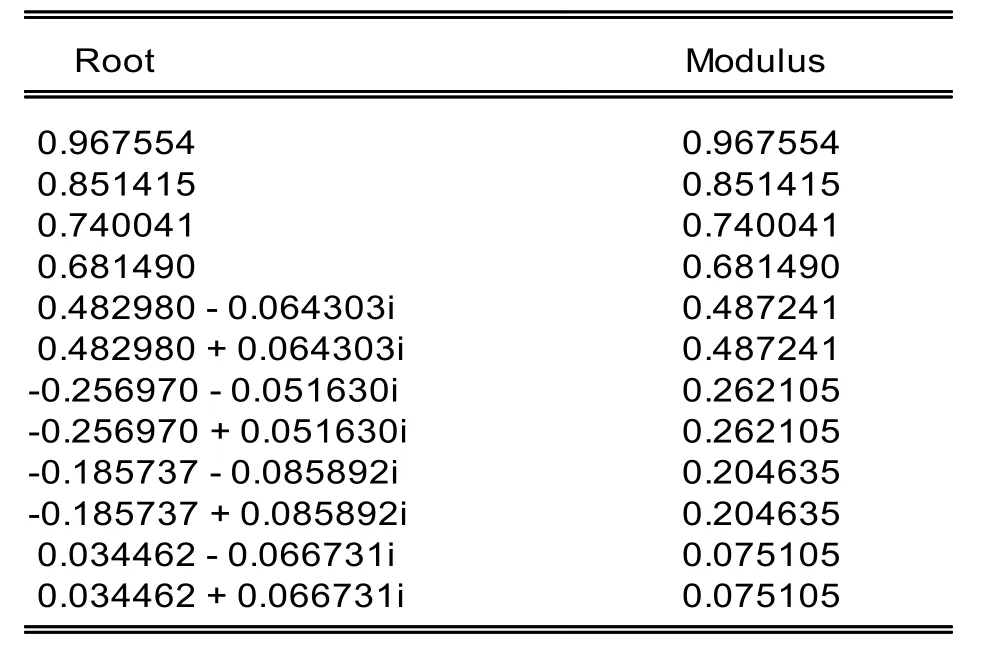
表3 方程特征根的检验

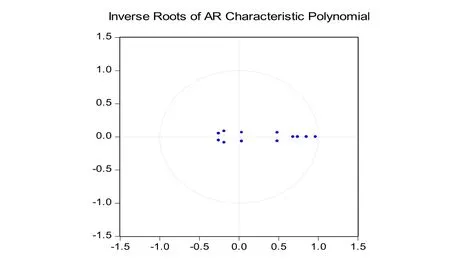
图1 方程特征根的检验

检验VAR模型的稳定性水平就是检验VAR模型所有特征根的模的倒数与1的关系或者特征根在单位圆的情况，从图1的左侧VAR（5）得出模型所有特征根的模都小于1，图1右侧所有的特征根都位于单位圆内，所以得出VAR（5）模型是平稳的。接下来进一步对乌鲁木齐市的PM2.5的影响因素进行脉冲响应分析，对各个变量对模型的冲击效果进行检验。

4.4 格兰杰因果关系检验

格兰杰因果关系的检验是对某变量的滞后项进行检验，看它是不是含在其他某变量的方程中，想要确定衍生污染物与PM2.5建立的长期的关系，从而找出适合治理空气的方案，得出他们长时间内存在的因果关系就是我们研究的目的。

结果可以看出的PM10、SO2、CO、NO、NO2、O3均为方程的格兰杰原因，接下来就是进行脉冲响应分析。

4.5 脉冲响应分析

由于VAR（p）模型不是以理论为依据，而是数据导向型的建模过程，所以模型中很多参数可能不具有明显的实际意义，因此需对模型的实际意义进行阐述；实际利用VAR（p）模型进行分析时，需要考虑某个变量残差的变动对它本身以及系统中其他变量的影响情况，所以运用广义脉冲响应函数对乌鲁木齐市PM2.5及其影响因素进行分析，选择分析期的长度为10期。运行结果如图2显示，其中蓝色实线表示脉冲响应函数的曲线，红色的虚线表示正负两倍的标准差置信带。

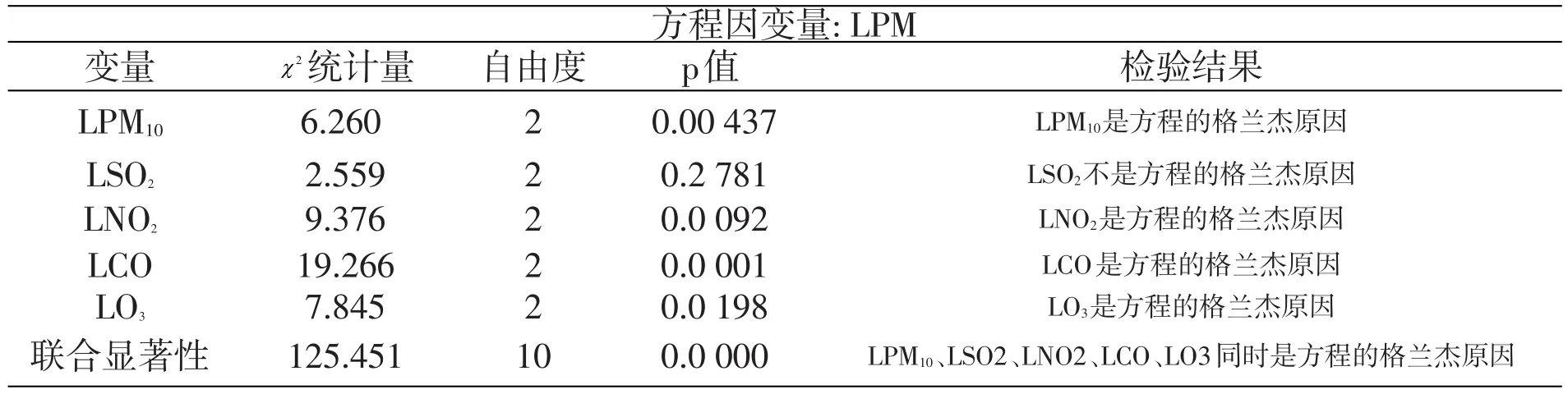
表4 granger因果检验结果

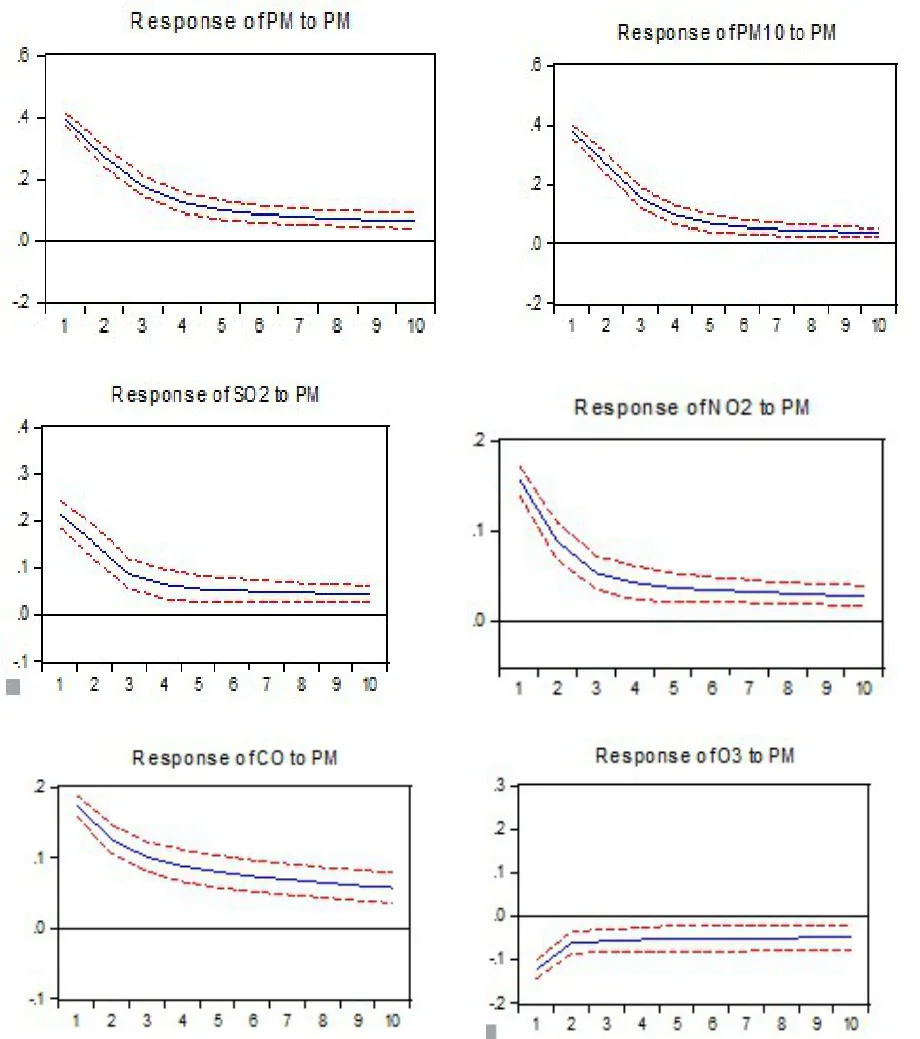
图2 乌鲁木齐市的PM2.5的影响因素进行脉冲分析

通过对模型VAR（5）的方程进行脉冲响应分析，选择的分析期为10期，结果通过脉冲分析图，在1期、2期O3、CO和NO2一个标准差的正向冲击会引起PM2.5浓度的较强的反应，其中O3的正向冲击会在第2期和第3期之间会带来PM2.5的负向变动，即对PM2.5产生抑制作用，并在第4期达到负项波动最高值-0.03，在第6期后影响渐趋于0，即影响作用的消失，SO2变动对PM2.5的影响作用相似，一个标准差正向冲击会给PM2.5带来带来正向变动，后期很快消失。总体为来自身的信息在第1期立刻有了较强的反应，产生最大正向影响，然后迅速减弱，到第10期反应基本消失。

4.6 方差分析

VAR模型中的方差分解是在研究每给出一个冲击时，造成的反应对内生的变量的变化的贡献率，从而得出不同的冲击对模型影响的重要性，这也显示出模型的动态特点，因此实际反应中各变量的贡献情况就可以了。

从表5可以看出，PM2.5在第1期只受到自身的影响，其中自身的方差贡献率是100%，其他的对PM2.5的方差贡献率则为0，从第2期开始，自身对方差的贡献率开始减小，其他的污染物对起作用开始增大，CO变动对PM2.5的影响作用不断加强，并在第10期对PM2.5的方差贡献率达到最大值13.4%，存在滞后效应，且持续时间较长。其次PM10变动对PM2.5的影响较大，在第10期达到5.52%，也就是说有效治理co污染有助于治理PM2.5间题，这符合乌鲁木齐的现有情况。

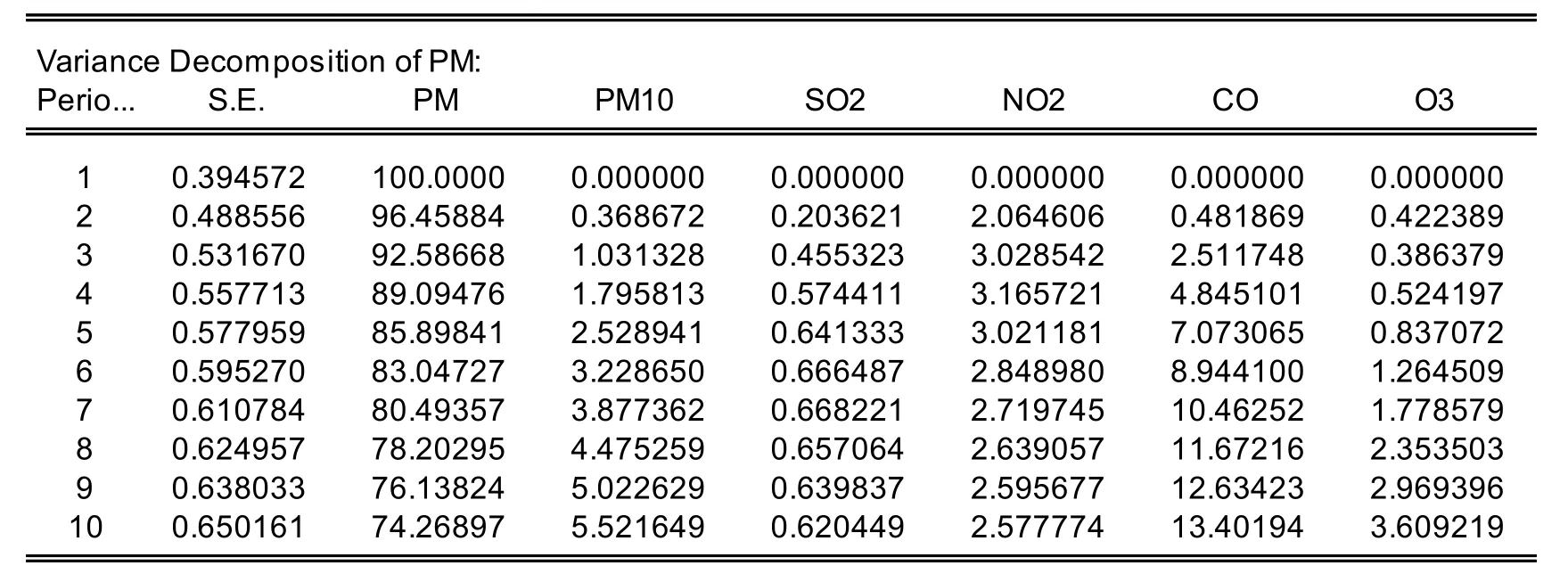
表5 方差分解图

5 结论

运用VAR模型，对乌鲁木齐市PM2.5与其它空气污染物之间的动态关系进行分析研究，基于构建的VAR（5）模型，及对其平稳性的检验，可得即使PM2.5与 SO2、NO2、PM10、CO 和O3这些变量同时受到内外的影响，但是它们所构成的空气质量系统稳定的；格兰杰因果关系显示，SO2、NO2、CO和O3是PM2.5的格兰杰原因；长期来说，SO2、NO2、CO和O3浓度值的变化会引起PM2.5浓度值的变化；最后广义脉冲响应函数分析和方差分解，又对PM2.5与SO2、NO2、PM10、CO和O3之间的短期动态关系进行分析；结果表明SO2、NO2、可吸入颗粒物、CO浓度值对PM2.5浓度值的影响持续的时间较长而且正向的影响关系，而 O3对 PM2.5的影响总体上是反向的，即 PM10、SO2、NO2、CO浓度值的增加会引起PM2.5浓度值的增加，O3浓度值的增加则会使PM2.5浓度值降低。