基于林木生长阶段的青冈栎生长方程研究
龙时胜,曾思齐,肖化顺,刘发林,刘 洵,向博文
(中南林业科技大学 林学院,湖南 长沙 410004)
林木生长方程是林木各项因子,包括直径、树高、材积、生物量等,随着林木年龄变化的函数。陆文杰[1](1981)提出用幂函数模拟林木生长方程,研究证明应用此类经验方程能较好的预测林木胸径的生长。唐守正[2](1998)从数学假设的角度分析了Richards方程模拟林木直径生长的可行性。目前林木生长方程的研究对象主要集中在杉科,松科等针叶林或人工林[3-4],对青冈栎这类阔叶次生林的研究较少,青冈栎林木生长方程的研究能够有效的预测林木的更新、生长以及估损的过程,为制定合理的经营措施等提供必要的理论依据。
林木生长阶段的划分,其目的是为了正确地揭示林木在一个生长周期内的不同生长阶段的生长特点,并针对不同阶段施以相应的经营措施。郑勇平[5]认为,随着年龄的变化,林木胸径、树高和材积的生长对外部环境条件的要求是变化的,并呈现出一定的阶段性。通常进行树木生长阶段的划分,是采用定性的方法,即凭经验在生长曲线的拐点处进行“分割”,这种划分方法有一定的人为因素,难免影响到划分的准确性。
青冈栎(Cyclobalanopsisglauca)属壳斗科青冈属常绿阔叶树种,它是我国亚热带常绿阔叶林带的主要优势树种,也是我国亚热带东部地区主要造林树种,适生范围广。20世纪中叶,青冈栎天然林遭遇大面积的砍伐破坏,目前分布的青冈栎林大多是砍伐后经封山抚育而形成的次生林,林分面积一般较小且林分质量低下。我国对于青冈栎的研究起步较晚,主要集中在生物量[6]、林木竞争[7]、种子形态与种苗抗性[8]等方面。因此,本研究以中南林业科技大学芦头实验林场的青冈栎次生林为研究对象,从定量的角度出发,采用有序聚类的方法[9]对青冈栎生长阶段进行划分,并分别构建各生长阶段的胸径与树高生长方程,以期提高生长方程对于青冈栎生长规律的预测效果,为青冈栎的提质增量提供一定的理论依据。
1 研究区概况
芦头实验林场(113°51′52″-113°58′24″E,28°31′17″-28°38′00″N)位于湖南省岳阳市平江县,属罗霄山脉北端,海拔124~1 272.5 m,多年平均日照时数1 731 h,年平均气温16.8℃,极端最高气温40.3℃(1971年7月26日),极端最低气温-2℃(1972年2月9日)。多年平均无霜期274 d左右,初霜期在11月上、中旬,终霜期在3月中旬左右。多年平均降水量1 624.8 mm,多年平均蒸发量为600~900 mm。林场属东亚热带向北亚热带过渡气候带,地貌类型以中山、低山为主,平均坡度25°左右,土壤以红壤和山地黄壤为主。森林群落上层主要以壳斗科(Fagaceae)、樟科(Lauraceae)、山茶科(Theaceae)、木兰科(Magnoliaceae)等为优势。
2 材料与方法
2.1 材料来源
2016年7月,在中南林业科技大学芦头实验林场设置16块青冈栎次生林固定样地,样地面积大小为20 m×20 m,主要调查了样地的立地条件、林下灌木与草本、土壤以及进行每木检尺工作。为分析该地区青冈栎的生长过程,在样地内分径阶共砍伐18株青冈栎解析木,其中12株解析木将用于直径与树高生长过程的拟合,6株解析木将用于生长方程的预测效果检验。解析木采用0.5 m区分段法进行树干解析,计算出各解析木的胸径、树高和材积的总生长量、连年生长量以及平均生长量,解析木的基本情况见表1。
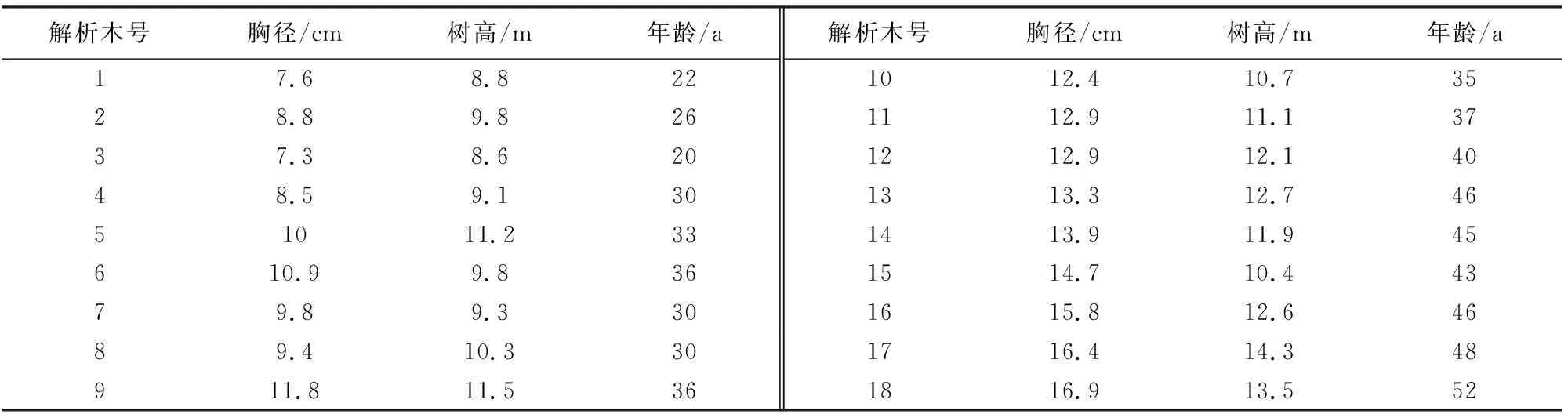
表1 解析木基本情况
2.2 研究方法
2.2.1 生长方程选择 青冈栎胸径与树高生长方程的拟合主要选用3个生长方程,包括1个树木生长经验方程——修正Weibull函数[10],以及2个树木生长理论方程——Logistic方程[11-12]和Richards方程[13-14]。这些生长方程通用性强、准确度高,且参数具有生物学意义,是目前应用较广泛的生长方程。
Logistic方程(1838年)
(1)
Richards方程(1959年)
Y=a(1-e-ct)b
(2)
修正Weibull函数(1978年)
Y=a(1-e-btc)
(3)
式中,Y为胸径、树高或材积,t为年龄,a,b,c为方程的参数。
2.2.2 有序聚类方法 聚类分析[15-16]是将一批样品或变量按照它们在性质上的亲疏程度进行分类,分类的方法很多。如直接聚类法是先把各个分类对象单独视为一类,然后根据距离最小的原则,依次选出一对分类对象,并成新类。如果其中一个分类对象已归于一类,则把另一个也归入该类;如果一对分类对象正好属于已归的2类,则把这2类并为一类。调试法是先将n个样品进行初步分类,然后以分类函数尽可能小的原则,对已分类别进行调整,直到分类合理为止。有序聚类[17]是在不打乱样本秩序的条件下对样本进行聚类分析,而树木按照年龄分布的生长速率即可看作有序样本,因此运用有序聚类对青冈栎生长阶段进行划分。
从定量的角度出发, 分别选取青冈栎直径与树高连年生长量作为变量,利用有序聚类的方法通过计算机软件处理分类。其基本原理为:某一类样品{(Xi,Xi+1…,Xj)i≤j}的直径即为该类样品的离差平方和,用D(i,j)表示。
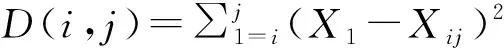
(4)
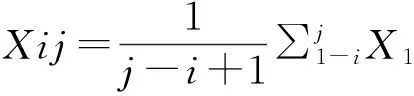
(5)
式中,D(i,j)为某一类样品的直径,Xi为有序样品为n维向量,Xij为某一类样品的均值,i为某一类样品起点,j为某一类样品终点。
n个样品分成m类的误差函数为:
(6)
即某种分法的误差函数为各类直径之和。当n和m固定时,φ[P(m,n)]越小,表示类内离差平方和越小,分类越合理。其最小误差函数为:
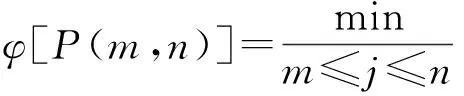
(7)
它表示n个样品分成(m-1)类的最优分法再加上最后(n+1-j)个样品形成的m类合并而成。而j可由m一直变到n,在这些可能中选一种最优的j,形成n个样品的最优分法。其中,n为样品总数,m为分类数,i为某一类样品起点,j为某一类样品终点。
2.2.3 方程检验 研究选取的总样本数为18株青冈栎解析木,其中12株作为生长方程的建模样本,6株作为方程的检验样本,方程检验的评价指标主要有决定系数R2,均方根误差RMSE,决定系数R2越大,说明拟合精度越高,均方根误差RMSE越小,说明模型预估值与真实值的误差越小。
(8)
(9)
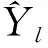
3 结果与分析
3.1 生长阶段的划分
3.1.1 生长过程分析 以12株青冈栎解析木为基础,采用修正Weibull函数、Logistic方程以及Richards方程对青冈栎直径与树高生长过程进行模拟,3个方程的参数及拟合效果见表2。
由表2可知,3个方程分别拟合青冈栎直径生长过程时,3个方程的决定系数R2均在0.85以上,说明青冈栎直径的生长与年龄关系显著。在模型拟合精度方面,Richards方程的决定系数R2达到0.897,高于修正Weibull函数与Logistic方程的决定系数R2;在模型的预测效果方面,Richards方程的均方根误差RMSE(1.42)少于修正Weibull函数与Logistic方程的均方根误差。3个方程分别拟合青冈栎树高生长过程时,3个方程的决定系数R2均在0.80以上,说明青冈栎树高的生长与年龄关系较显著,在模型拟合精度方面,修正Weibull函数的决定系数R2达到0.813,高于Richards方程与Logistic方程的决定系数R2;在模型的预测效果方面,修正Weibull函数的均方根误差RMSE(1.40)少于修正Richards方程与Logistic方程的均方根误差。

表2 直径与树高生长方程拟合结果
比较分析3个方程对于青冈栎直径与树高的生长过程可知,Richards方程对青冈栎直径生长的拟合效果最佳,修正Weibull函数对青冈栎树高生长的拟合效果最佳,2个方程的公式为:
D=36.8×(1-e-0.014 4A)1.224 7
(10)
H=20×(1-e-0.051 6×A0.756 6)
(11)
式中,D为直径,H为树高,A为林木年龄。
3.1.2 有序聚类分析 由于18株解析木中年龄最大为52 a,青冈栎直径与树高生长方程对于52 a以上的林木可能预测效果不佳,因此在用有序聚类划分生长阶段时,只考虑1~52 a的林木生长状况。以青冈栎4 a为一个龄级,共划分为13个龄级,将不同龄级Ⅰ(1~4 a),Ⅱ(5~8 a),…,ⅩⅢ(49~52 a)分别定义为X1,X2…X13系列。运用直径与树高生长方程计算得出各个龄级的直径与树高连年生长量,进行初始样本的分配如表3。
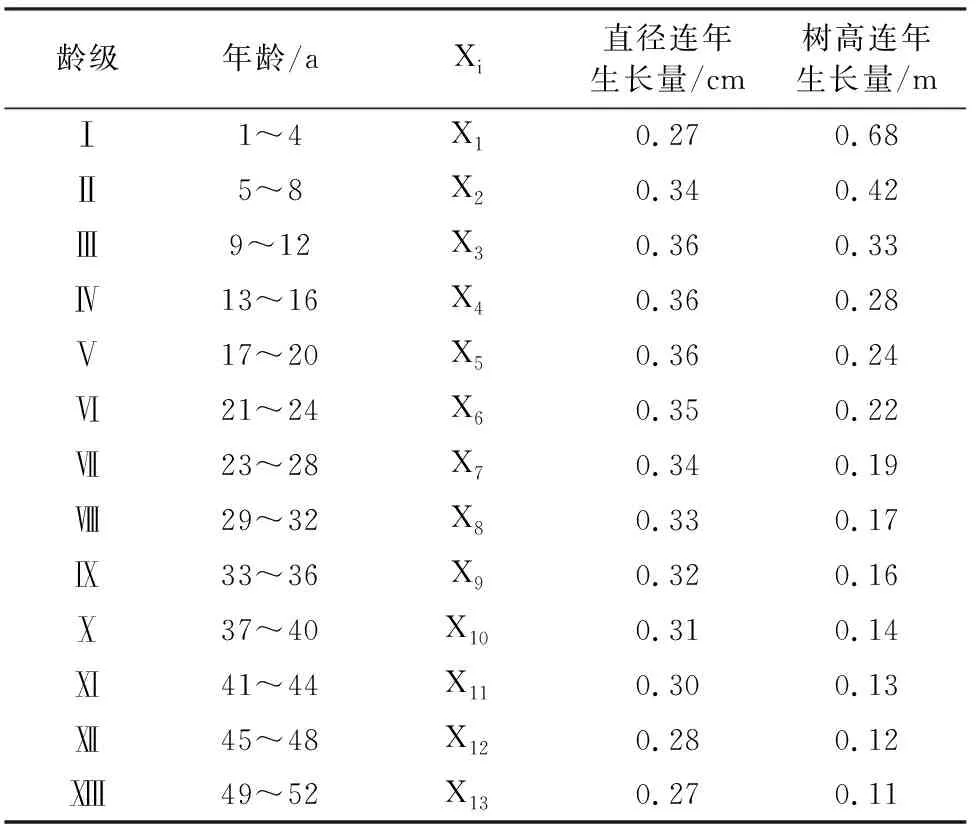
表3 有序聚类分析的样本分配
由表3可知,直径连年生长量随着年龄的增大呈先增后减的趋势,在第20年时,直径连年生长量达到最大(0.36 cm/a);树高连年生长量随着年龄的增大而减少,依据直径或树高的连年生长量情况,我们难以定量的判断出青冈栎的生长阶段。
运用DPS数据处理系统中的有序样本最优分割法分别对直径与树高连年生长量进行计算,输出结果见表4。
由表4可知,按直径连年生长量划分青冈栎生长阶段时,当分类数为2,最优分割结果为X1~X9,X10~X13,也就是136 a为第1阶段,3 752 a为第2阶段,当分类数为3时,依次类推;按树高连年生长量划分青冈栎生长阶段时,当分类树为2,最优分割结果为X1~X2,X3~X13,也就是1~8 a为第1阶段,952 a为第2阶段,当分类数为3时,依次类推。
3.1.3 生长阶段划分 林木生长阶段一般分为幼龄、中龄、近熟龄、成熟龄4类。由于青冈栎生长缓慢,所砍伐的18株解析木中,青冈栎材积平均生长量曲线与连年生长量曲线没有相交,且研究区内近熟龄,成过熟龄林较少,无法判定该地区青冈栎的数量成熟龄以及近、成过熟龄的年龄节点,因此,本研究考虑将青冈栎生长阶段仅划分为幼龄林和中龄林2个生长阶段,也就是按分类数为2对青冈栎生长阶段进行划分,分别按直径连年生长量与树高连年生长量划分的青冈栎生长阶段见表5。

表4 有序聚类分析的计算结果
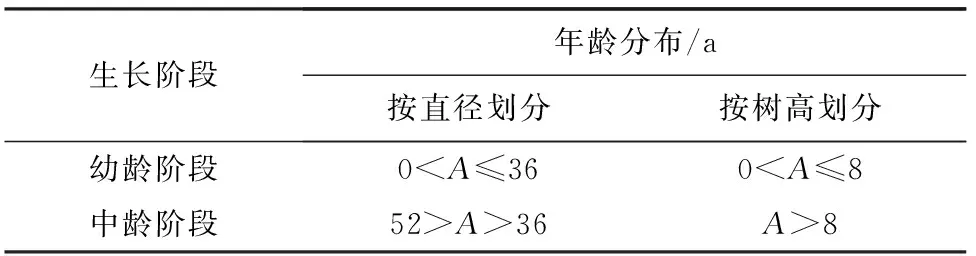
表5 各生长阶段的年龄分布
3.2 不同分类方法下的生长方程构建
3.2.1 按直径划分生长阶段 依据林木直径连年生长量,采用有序聚类的方法对青冈栎生长阶段进行划分,幼龄阶段为136 a,中龄阶段为3 752 a。本研究分别幼龄阶段与中龄阶段拟合胸径的生长方程,即12株建模解析木中,年龄在136 a的解析木构建生长方程,年龄在3 752 a的解析木构建另一个生长方程。分别采用修正Weibull函数、Logistic方程以及Richards方程拟合青冈栎幼龄与中龄阶段的生长方程,拟合结果见表6。
由表6可知,拟合幼龄阶段的胸径生长方程中,Richards方程在评价指标决定系数R2(0.898)与均方根误差RMSE(1.30)上均优于修正Weibull函数与Logistic方程;拟合中龄阶段的胸径生长方程中,Logistic方程在评价指标决定系数R2(0.882)与均方根误差RMSE(0.58)上均优于修正Weibull函数与Richards方程,因此,可以确定幼龄阶段的最优胸径生长方程为Richards方程,中龄阶段的最优胸径生长方程为Logistic方程,2个方程公式为:
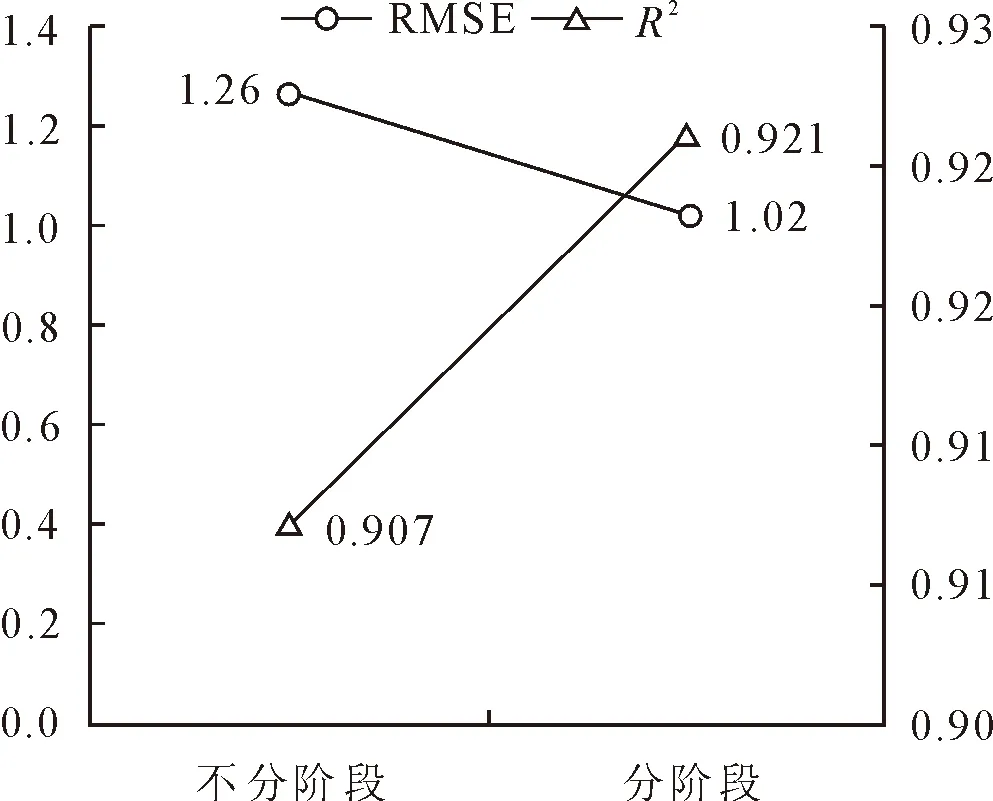
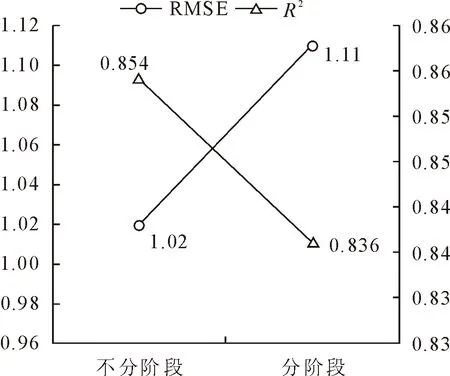
D幼=25.1×(1-e-0.023 5A)1.332 2(0 (12) (13) 式中,D幼为幼龄阶段的林木直径,D中为中龄阶段的林木直径,A为林木年龄。 3.2.2 按树高划分生长阶段 依据林木树高连年生长量,采用有序聚类的方法对青冈栎生长阶段进行划分,幼龄阶段为18 a,中龄阶段为952 a。本研究分别幼龄阶段与中龄阶段拟合树高的生长方程,即12株建模解析木中,年龄在1~8 a的解析木构建生长方程,年龄在952 a的解析木构建另一个生长方程。分别采用修正Weibull函数,Logistic方程以及Richards方程拟合青冈栎幼龄与中龄阶段的树高生长方程,拟合结果见表7。 表6 胸径生长方程拟合结果 表7 树高生长方程拟合结果 由表7可知,拟合幼龄阶段的树高生长方程中,Logistic方程在评价指标决定系数R2(0.798)与均方根误差RMSE(0.59)上均优于修正Weibull函数与Richards方程;拟合中龄阶段的树高生长方程中,Logistic方程在评价指标决定系数R2(0.758)与均方根误差RMSE(1.41)上均优于修正Weibull函数与Richards方程,因此,可以确定幼龄阶段的最优树高生长方程为Logistic方程,中龄阶段的最优胸径生长方程为Logistic方程,2个方程公式为: (14) (15) 式中,H幼为幼龄阶段的林木直径,H中为中龄阶段的林木直径,A为林木年龄。 本研究基于直径连年生长量与树高连年生长量,采用有序聚类方法分别对青冈栎生长阶段进行划分,并分别构建了幼龄阶段与中龄阶段的胸径与树高生长方程,但分阶段构建的生长方程在预测精度方面是否优于不分阶段构建的生长方程?研究利用检验样本(6株青冈栎解析木)对2种方法构建的生长方程的预测效果进行对比分析。 3.3.1 胸径生长方程的对比分析 基于6株青冈栎解析木检验样本,利用不分阶段构建的生长方程(4)计算各年龄下的胸径预估值,同样利用分阶段构建的生长方程(6)、方程(7)计算各年龄下的胸径预估值,将两组胸径预估值与胸径真实值进行比较分析,结果见图1。 图1 胸径生长方程预测效果比较 由图1可知,与不分阶段构建的生长方程相比,分阶段构建胸径生长方程后,模型预估值与真实值拟合时,决定系数R2由0.907提高到0.921,预测精度提高;预估值与真实值的均方根误差RMSE由1.26降低到1.02,误差降低,说明按直径划分生长阶段后,分阶段构建胸径生长模型能更好地预测青冈栎直径的生长。 3.3.2 树高生长方程的对比分析 基于6株青冈栎解析木检验样本,利用不分阶段构建的生长方程(5)计算各年龄下的树高预估值,同样利用分阶段构建的生长方程(8)、方程(9)计算各年龄下的树高预估值,将2组树高预估值与树高真实值进行比较分析,结果见图2。 图2 树高生长方程预测效果比较 由图2可知,与不分阶段构建的生长方程相比,分阶段构建树高生长方程后,模型预估值与真实值拟合时,决定系数R2由0.854降低到0.836,预测精度降低;预估值与真实值的均方根误差RMSE由1.02增加到1.11,误差增大,说明按树高划分生长阶段后,分阶段构建树高生长模型不能更好的预测青冈栎树高的生长。 有序聚类的方法划分林木生长阶段简便易行,且能反映林木的实际生长情况。熊泽彬[9]研究发现,利用有序聚类方法可将杉木生长过程划分为幼龄110 a,中龄1 120 a,近熟龄2 126 a,成过熟龄25 a以上。魏蕾[11]研究中利用有序聚类方法将I-69杨划分为缓苗期、生长初期、速生期和生长后期。在本研究中,通过有序聚类的方法分别对青冈栎直径与树高连年生长量进行分析,依据直径连年生长量对青冈栎生长阶段进行划分的结果为青冈栎幼龄阶段136 a、中龄阶段3 752 a;依据树高连年生长量对青冈栎生长阶段进行划分的结果为青冈栎幼龄阶段18 a、中龄阶段952 a。 林永英[18]利用青冈栎树高划分了林木生长阶段,曹帮华[19]利用苗高对刺槐生长规律进行了研究,但研究中都没有分析利用直径划分生长阶段的可行性。本研究分析了分别以直径和树高划分林木生长阶段的准确度,并对各生长阶段构建了生长方程,结果表明:依据直径连年生长量划分生长阶段后,利用幼龄与中龄阶段的生长方程预测青冈栎的直径生长,能够减少预测误差,显著的提高生长预测的精度;依据树高连年生长量划分生长阶段后,利用幼龄与中龄阶段的生长方程预测青冈栎的树高生长,模型精度降低。因此,利用有序聚类的方法,依据直径连年生长量对青冈栎生长阶段进行划分,并分别生长阶段构建生长方程,能够有效的提高生长预测精度,对青冈栎的经营研究与提质增量具有一定的参考价值。 研究区的青冈栎次生林主要为中幼龄林,近成熟龄林较少,选取的解析木直径与年龄均相对较小,因此本研究仅将青冈栎生长阶段划分为幼龄与中龄,这在一定程度上限制了生长方程的使用范围。后续研究将扩大样本的数量与年龄范围,对青冈栎幼龄、中龄、近熟龄、成过熟龄4个生长阶段的生长规律做进一步的研究。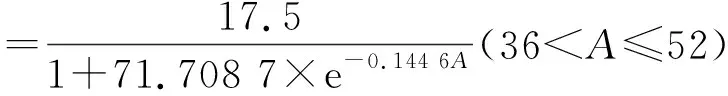


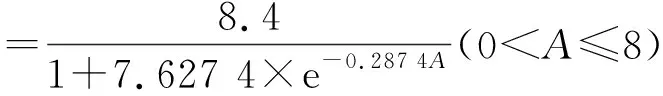
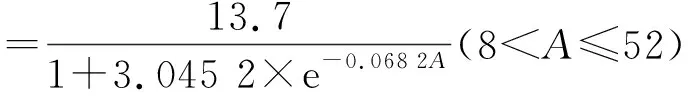
3.3 模型效果检验
4 结论与讨论

