基于智能全站仪的地铁隧道自动化监测精度分析及验证
柏文锋
(广州地铁设计研究院有限公司,广东 广州 510010)
为了掌握地铁周边施工,尤其是深基坑工程施工对地铁隧道结构的影响,需要对地铁隧道结构进行定期甚至连续的动态监控测量。根据相关技术规范、规程及地方规定的要求,各城市对地铁结构安全保护的要求越来越高,多个城市明确要求在地铁保护控制区内施工时,在风险较高的情况下,需对地铁结构状况进行自动化监测。地铁隧道的自动化监测方法很多[1-2],目前国内外使用最多、最成熟的方法是利用智能全站仪实施的动态监测[3-8]。智能全站仪作为一种能够进行目标自动搜索、识别、跟踪和精确照准并获得角度、距离和三维坐标等信息的测量设备,在变形监测领域得到了广泛的应用[9-10]。地铁隧道空间狭长,基准点和监测点都只能分布在狭长的隧道两端,同时地铁隧道变形监测的精度要求较高,此时智能全站仪能否满足监测精度的需求,暂时还没有在实际的隧道工程环境下对监测结果进行专门的量化验证。本文从基于智能全站仪的地铁隧道监测的数学模型出发,对该方法的理论监测精度进行分析,并以此为指导在某地铁隧道对所能达到的监测精度进行实际验证。
1 基于智能全站仪的地铁隧道监测精度分析
基于智能全站仪的地铁隧道自动化监测方法如图1所示,在隧道两端设置基准点,利用自由设站法[11]通过瞄准多个已知基准点计算得到安置于测站点的智能全站仪的坐标,然后利用极坐标测量方法[12]观测得到多个监测断面的监测点的三维坐标。
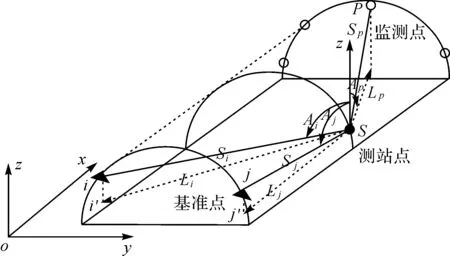
图1 智能全站仪地铁隧道监测示意图
1.1 自由设站法
自由设站法是在测站点上安置全站仪,并观测多个已知基准点的方向和距离,按间接平差方法计算测站点坐标的一种测量方法。间接平差以待定测站点的坐标作为未知参数,根据各类观测值建立相应的误差方程,然后基于最小二乘原理计算测站点的坐标平差值。在采用自由设站法计算测站点的坐标时,可以把平面和高程坐标分开平差,而更严密的平差模型则是以斜距、水平方向和天顶距为原始观测值,以测站点的三维坐标作为未知参数进行平差[13-15]。
如图1所示,在测站点S观测i点,获得相应的水平方向、天顶距和斜距观测值Li、Ai及Si,根据间接平差模型对这3类观测值列误差方程式如下
(1)
(2)
(3)
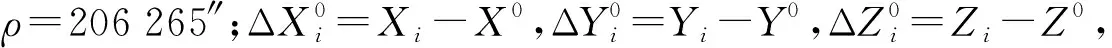
根据上述水平方向、天顶距和斜距3类观测值的误差方程及基准点的个数n,可得到观测量误差方程的系数矩阵B3n×4和常数向量矩阵L3n×1,则误差方程的矩阵形式为
V=BdX-L
(4)
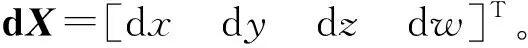
按最小二乘原理,解误差方程得到
dX=(BTPB)-1BTPL
(5)
可得自由设站法测站点的三维坐标及定向角的平差值为
(6)
单位权中误差σ0估值为
(7)
(8)
自由设站法在确定观测值的权时,可按全站仪的标称精度来定权,取水平方向观测中误差mL为单位权中误差,即m0=mL,则各类观测值相应的定权公式为
(9)
1.2 极坐标法
如图1所示,在地铁隧道监测的坐标系建立中,一般选定坐标系X轴沿隧道纵向,Z轴沿铅垂方向。此时各监测断面的监测点Y轴的变化量即为隧道径向方向的变形量,Z轴方向的变化量即为隧道拱顶沉降或隧道底板沉降。
通过自由设站法得到测站点的三维坐标之后,各监测点的坐标可通过极坐标法测量得到[16]。具体的计算公式如下
(10)
式中,(XP,YP,ZP)为监测点的坐标;(X,Y,Z)为测站点的坐标;SP为斜距观测值;AP为天顶距观测值;LP为水平方向观测值;w为定向角。
监测过程中由于智能全站仪采用强制对中,目标棱镜也始终固定在隧道断面上,故可不考虑对中误差和目标偏心误差。根据误差传播定律,可得到监测点P各方向的坐标值的精度如下

(11)
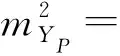
(12)
(13)
式中,mX、mY、mZ为测站点各方向的中误差;mw为定向角的中误差;mS、mA、mL分别为斜距、天顶距及水平方向观测值的中误差。mX、mY、mZ、mw可以根据自由设站计算得到,mS、mA、mL可由观测仪器的标称精度获取。
2 监测精度的实际验证
为了验证智能全站仪应用于地铁隧道监测的实际精度,选取了广州地铁6号线某隧道区间进行测试。测试过程中所选择的智能全站仪型号为Leica TCRP 1201,其标称测距精度为1 mm+1.5×10-6D,方向测量值精度为1″。
在实际测试中,设计了一个可活动的杆件与监测小棱镜相连,通过人工调整加入位移量并与智能全站仪的测量结果进行对比来验证其精度。在距离测站点10、50、100、150 m处各布设1个监测断面,在每个断面上安置2个活动杆件,在杆件上安装监测小棱镜。断面点命名规则T101、T102(字母T代表测试,第一个数字1代表断面号,后两位数字01代表该断面点编号),如图2所示,每个断面布设两个监测点,分别位于地铁隧道道床及侧墙上。在安装杆件时,T101位置的杆件尽量保持水平,用于探测Y方向的径向变形;T102位置的杆件安装尽量铅垂,用于探测Z方向的竖直变形。

图2 断面监测点杆件安装示意图
杆件在各断面安装完成之后,在隧道观测墩安置仪器,通过自由设站法和极坐标法对基准点和各监测断面进行学习测量,并将计算得到的监测小棱镜的三维坐标作为初始值用于后期计算变形量。在自动监测阶段,一共进行了3期观测,每期观测之前都对各断面与监测小棱镜相连的活动杆件进行调整,人工加入一定的位移量并用游标卡尺进行量测,用于和智能全站仪的测量结果进行对比。各断面Z方向的对比结果如图3所示。

图3 各断面Z方向的监测精度对比
以游标卡尺测量的变化量为真值,智能全站仪的监测结果与之求差来分析智能全站仪的监测精度。由图3的对比结果可以看出,在10、50 m断面处智能全站仪的Z方向变形量监测精度优于0.5 mm。随着断面与测站的距离增加,智能全站仪的Z方向的监测精度降低,断面100 m处的监测点的精度稍高于1 mm,而在150 m处全站仪Z方向的监测精度接近2 mm。根据相关规范要求,若采用上述精度的智能全站仪监测隧道拱顶或隧道底板沉降,最佳监测范围为100 m以内。
各监测断面Y方向的对比结果如图4所示。由图中可以看出,与Z方向的监测精度类似,随着断面与测站的距离增加,智能全站仪Y方向的监测精度有逐渐降低的趋势。测试中在10、50、100 m断面处各期Y方向的监测精度均优于1 mm,而在150 m断面处各期Y方向的监测精度则降低到2 mm左右。结合地铁隧道径向形变的监测精度要求,在断面距离测站100 m的范围内,上述标称精度的智能全站仪可满足监测需求。
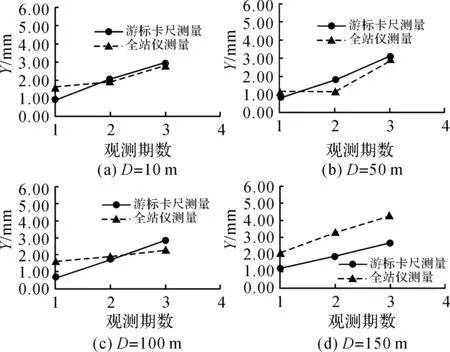
图4 各断面Y方向的监测精度对比
3 结 语
智能全站仪在地铁隧道结构的几何变形监测中应用越来越广泛,而其监测精度也备受关注。本文结合全站仪变形监测的基本数学模型,分析了其应用于地铁隧道监测的精度情况,并运用智能全站仪在实际的地铁隧道进行了试验验证。结果表明,采用测距精度为1 mm+1.5×10-6D,方向测量值精度为1″的智能全站仪,对于地铁隧道拱顶或底板沉降和径向形变的最优监测范围为100 m以内,若采用精度更高的设备,则有望进一步增大监测范围。

