有界约束平差模型的变量代换方法

张立艳

(成都农业科技职业学院，四川 成都 611130)

在大地测量及相关领域，随处可见一些能用不等式约束表示的先验信息。如在大坝变形分析中，可以根据控制点的位移方向建立形变量的不等式约束[1]；利用GPS进行高层建筑物变形监测时，可以根据双差观测值的精度和建筑物的最大形变量构造模糊度的不等式约束搜索空间[2]；在方差分量估计中，所有的方差分量均为正值[3]。合理利用有效的先验约束信息，能提高参数估计的精度和可靠性。不等式约束平差模型在最优化理论中等价于二次规划，可以采用起作用集算法、序列二次规划法和罚函数方法求解[4]。在测量领域，卢刚运用奇异值分解给出了不等式约束平差的最小距离方法[5]。朱建军将模型参数视作不等式约束区间上服从均匀分布的随机变量，给出了基于均值、众数和最小距离的贝叶斯解及其均方误差[6]。RAO将不等式约束转化为椭圆约束，采用极大极小准则给出了参数的有偏估计[7]。朱建军基于罚函数方法给出了不等式约束平差的一种简单迭代算法[1]。彭军还将多个不等式约束转化为单个凝聚约束，将不等式约束平差问题化为等式约束的非线性规划问题，并推导了参数估计的近似方差、均方误差矩阵及单位权方差[8]。

将不等式约束最小二乘平差问题转化为无约束极小化问题，罚函数方法是一种有益的尝试。凝聚约束方法也可以归结为求无约束最优化问题的解。以上两种方法都是对不等式约束条件的转换。不同于上述对约束条件进行转换，本文针对模型参数进行变量代换[9-10]，从而将约束最小二乘平差转化为无约束非线性规划问题，并采用一种常见的拟牛顿型算法即BFGS方法[11]进行参数估计。

1 有界约束平差模型及有效集方法

在测量数据处理中，一般是将含有误差的观测值表示为待估参数的函数，如式(1)中的上式。若预先得到全部或部分参数的上下确界，则可以建立如式(1)的下式所示约束。有界约束平差模型为

(1)

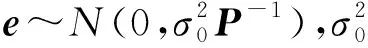
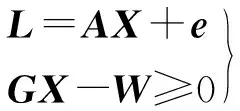
(2)

为了求解式(2)的最优估计值，根据最小二乘准则，在不等式约束的范围内，令观测值的误差平方和最小，从而得到如下的约束最优化问题

(3)

这里给出一种常见的解模型式(3)的起作用集方法。它在每次迭代中，以已知的可行点为起点，把在该点起作用约束作为等式约束，在此等式约束下极小化目标函数，求得新的比较好的可行点后，再重复上述步骤[4]。设在第k次迭代中，已知可行点X(k)，在该点起作用约束指标集为I(k)，解等式约束问题

(4)

模型式(4)可以按照附有限制条件的间接平差模型得到新的最优解X(k′)，然后将X(k′)代入所有的不等式约束条件进行判断。

(1) 如果X(k′)是可行点，且X(k′)-X(k)≠0，则在第k+1次迭代中，新的已知点取作X(k+1)=X(k′)。

(2) 如果X(k′)不是可行点，则令搜索方向为d(k)=X(k′)-X(k)，并沿着该方向进行搜索。

若迭代结束后，有效约束集对应的所有拉格朗日乘子都大于等于0，则X(k)是模型式(4)的最优解。若存在小于0的拉格朗日乘子，则将拉格朗日乘子取最小值所对应的约束从可行集中删除后重新迭代计算。

2 有界约束平差模型的变量代换方法

求解约束极值问题时，要兼顾目标函数值下降且满足约束条件，而无约束极值问题只要求满足目标函数值下降。因此，约束极值问题的求解比相应的无约束极值问题更为复杂。这里根据有界约束的特殊性，将处于有界约束中的参数进行变量代换，新的变量在整个实数空间中取值，从而将约束极值问题转换为无约束极值问题。下面给出两种实现有界约束参数的变量代换方法。

2.1 反正切变换

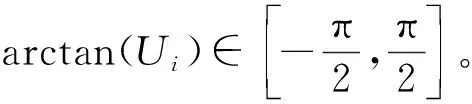
Xi=Wi1+(Wi2-Wi1)×(arctan(Ui)+π/2)/π

(5)

可以得知式(5)右端项的取值范围为[Wi1,Wi2]。Ui和Xi的函数关系如图1所示。

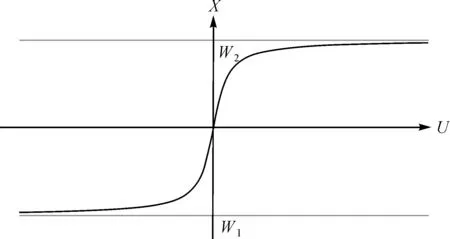
图1 经反正切变换后新变量与原变量关系

2.2 正弦变换

一般来说，具有上下界的函数，其变换方式并不是唯一的。构造如下的正弦函数

Xi=Wi1+(Wi2-Wi1)×(sinUi+1)/2

(6)

同理，正弦函数的定义域为整个实数空间，而它的值域sinUi∈[-1,1]。式(6)右端项的取值范围为[Wi1,Wi2]。Ui和Xi的函数关系如图2所示。

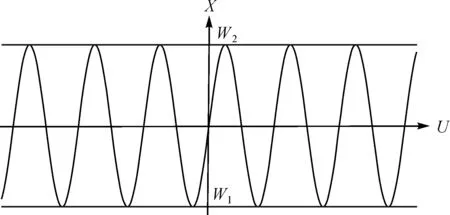
图2 经正弦变换后新变量与原变量关系

将具有上下约束的参数按照式(5)或式(6)进行变量代换以后，新的变量都是在整个实数空间内取值。然后，将新变量Ui代入式(1)中的上式，得到一个非线性观测方程，在最小二乘准则下，解无约束非线性极小化问题可以得到新变量的极值，再代入式(5)或式(6)可得到原变量的参数估值。

对于无约束非线性最优化问题，一种常用的方法是拟牛顿方法。它的基本思想是：用不包含二阶导数的矩阵近似当作牛顿法中Hessian矩阵的逆矩阵。其中BFGS方法是目前最流行有效的拟牛顿算法，采用BFGS方法求解非线性函数f(x)的极小值的一般步骤为[11]：

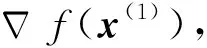
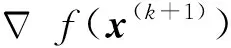
(5) 令k=k+1，转步骤(1)。

对于凸函数的最优化问题，采用精确线搜索，BFGS方法具有全局收敛特性，是一类具有较好数值效果和快速收敛的非线性最优化方法。

3 算例分析

在式(1)中，模拟如下算例

同时附加两个不等式约束条件：1.20≤x1≤1.30，2.50≤x3≤2.60。设观测值都为等权不相关观测值，即观测值的权矩阵为单位矩阵。当不考虑约束时，最小二乘解为

然后，采用本文提出的新方法，将约束变量分别进行如下变量代换

(7)

(8)

将中间变量分别代入式(7)，可得

同样，采用正弦代换式进行计算，初始值与反正切代换时相同，经过26次迭代，得到无约束解

将中间变量代入式(8)，可得到与反正切变换完全相同的解，且与起作用集方法的解结果相同。可见，有界约束的变量代换法求解有界约束平差模型是可行的。

4 结论与展望

对于只含上下有界约束且约束间互不相关的一类特殊不等式约束平差模型，本文提出将含有约束的参数进行变量代换，形成无约束非线性最优化问题。采用BFGS算法解上述问题，得到新变量的最优值，进而得到不等式约束最小二乘平差问题的解。但该方法目前只适用于模型参数是有界约束的情况，将该方法扩展到一般不等式约束的情况是下一步研究的方向。