一种基于多层感知器的动态区域联合短时降水预报方法
张鹏程 贾旸旸
(河海大学计算机与信息学院 江苏 南京 211100)
0 引 言
降水是多尺度大气系统共同作用的结果,受热力、流场、地形等多方面因素影响,复杂的物理形成机制使降水成为最难预报的天气要素之一。目前,降水预报方法主要分为两类:(1) 基于物理形成机制的预报方法;(2) 数据驱动的预报方法。
基于物理形成机制的预报方法主要是数值预报,由于大量的数据和计算的复杂性,数值预报往往需要大型计算机实现。数值预报目前已成为业务的重要依据,我国业务中常用的数值预报模式包括欧洲中期天气预报中心数值预报模式ECMWF、日本气象厅数值模式等。由于初始条件和边界条件等因素产生的不确定性,数值模式与实况始终存在偏差。
数据驱动的降水预报方法主要包括统计学方法和机器学习方法。时间序列分析是一种典型的多元统计分析方法,时间序列分析用于降水预报是基于降水的时间序列特性[1-2],如小波分析法(Wavelet)、自回归积分滑动平均模型ARIMA(Auto-regressive Integrated Moving Average Model)、马尔可夫模型(Markov Model)等。这类统计方法单纯从降水序列出发,没有考虑到气候或环境因素对降水的影响,只能从趋势上把握降水变化的大致方向。机器学习能够学习出气象或物理因子和降水之间的关系。降水预报中常用的机器学习方法包括支持向量机SVM、支持向量回归SVR、灰色预测方法、人工神经网络ANN等[3-5]。ANN是机器学习领域中最为活跃的分支之一,是有效的分类、拟合和标记算法。传统的用于降水预报的ANN模型包括前馈神经网络、BP神经网络BPNN、径向基函数神经网络RBFNN等[6-8]。为了区别于传统的ANN结构,深度学习DL和深层神经网络DNN的概念用来定义结构更为复杂、层次更为深厚的网络。
近年来,DL在图像识别、语音识别、自然语言处理等领域快速发展[9-11],相比于传统的ANN,DNN可以有更强的学习能力[12]。常见的DNN包括多层感知器MLP、深度信念网络DBN、长短期记忆网络LSTM、卷积神经网络CNN等。Lin等[13]将MLP用于台风降水预测,首先通过自组织映射算法对台风影响因子分类,再以此作为MLP的输入,降水作为MLP的输出,有效预测了台风降水。张鹏程等[14]以7个环境物理量作为DBN神经网络的输入,未来24小时降水量作为输出,通过在贵州遵义地区的实验证明了模型的有效性。Mekanik等[15]分析了ENSO和IOD两类气候因子与维多利亚地区春季降水的关系,并分别基于多元线性回归和MLP预测春季降水,发现MLP的泛化性能和准确率均优于多元线性回归模型。
目前,基于DL的降水预报方法通常以某一地区的因子和降水分别作为网络的输入和输出,没有考虑到不同地区之间的联系和降水系统的空间性质。本文在预报中心地区(站点)和周围地区(站点)之间建立多层感知器,通过主成分分析PCA方法对大气环流背景场和局地气象要素差异等13个因子降维,作为MLP的输入,并采用贪心算法确定MLP结构。通过联合多个MLP同时预报降水,提出了一种动态区域联合短时降水预报模型DRCF(Dynamic Regional Combined Short Time Rainfall Forecasting Model)。
1 主成分分析与MLP
1.1 主成分分析
主成分分析是多元统计学中常用的一种数据预处理和降维方法,问题变量个数太多会增加处理的复杂性[17]。PCA可以用较少的变量代表较多的信息。PCA可以删除变量的重复关系,建立尽可能少的新变量,使得这些新变量是两两不相关的,同时尽可能多得保持原有的信息。PCA的计算公式如下:
(1)
式中:X=(X1,X2,…,Xp)表示p个原始变量;Z=(Z1,Z2,…,Zp)表示p个新的变量。通过选择合适的μ,可以使得Z的各个因子之间不相关,同时主要的信息量集中到Z的前几个分量中,此时可以用Z的前几个分量代替X。μ的计算通常采用原始变量的相关系数矩阵计算,μ在数值上等于相关系数矩阵特征向量的组合。
1.2 MLP结构与调整算法
MLP是DNN中一种比较有代表性的网络[23]。MLP有很多层,第一层是输入层,最后一层是输出层,中间称为隐含层,每一层包括确定数目的神经元。MLP的神经元采用层内无连接,层间全连接的连接方式。图1是一个双隐含层的MLP结构示意图,图中输入层共有n1个结点,隐含层1和隐含层2分别有n2和n3个神经元,输出层有n4个神经元,除去输出层,每一层均有一个偏置结点。

图1 MLP结构示意图
MLP的前馈计算过程从输入层依次计算到输出层。对于一个输入、输出维数分别为n1、nm+2,且含有m个隐含层,每一个隐含层的节点数分别为(n2,n3,…,nm+1)的MLP,前馈过程中每个节点值得计算方法如下:
xij=f(WiXi-1+bi-1)
(2)
式中:xij代表第i层第j个神经元的值;Wi为第i-1层到第i层第j个神经元的权值向量;Xi-1为第i-1层所有神经元的值向量;bi-1表示第i-1层的偏置;f为激活函数。激活函数采用sigmoid函数:
(3)
MLP是典型的有监督学习算法,它的损失函数定义为:
(4)
式中:h为MLP的输出值;y为实际值;‖·‖是任一种距离范数,通常取2范数。
一般通过梯度下降法调整参数(包括权值和偏置),使得损失函数达到最小,本文MLP的参数调整算法采用动量BP算法。梯度计算和动量BP算法的计算方法如下:
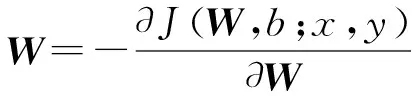
(5)
δWt=α▽Wt+βδWt-1
(6)
式(5)是梯度的计算方法;式(6)中α和β分别取(0,1)之间,本文均取0.5。
2 动态区域联合短时降水预报方法
DRCF主要包括3个部分:数据收集和预处理、MLP网络结构确定和参数调整、动态调整范围参数以及模式对比。图2显示了DRCF的建立过程。
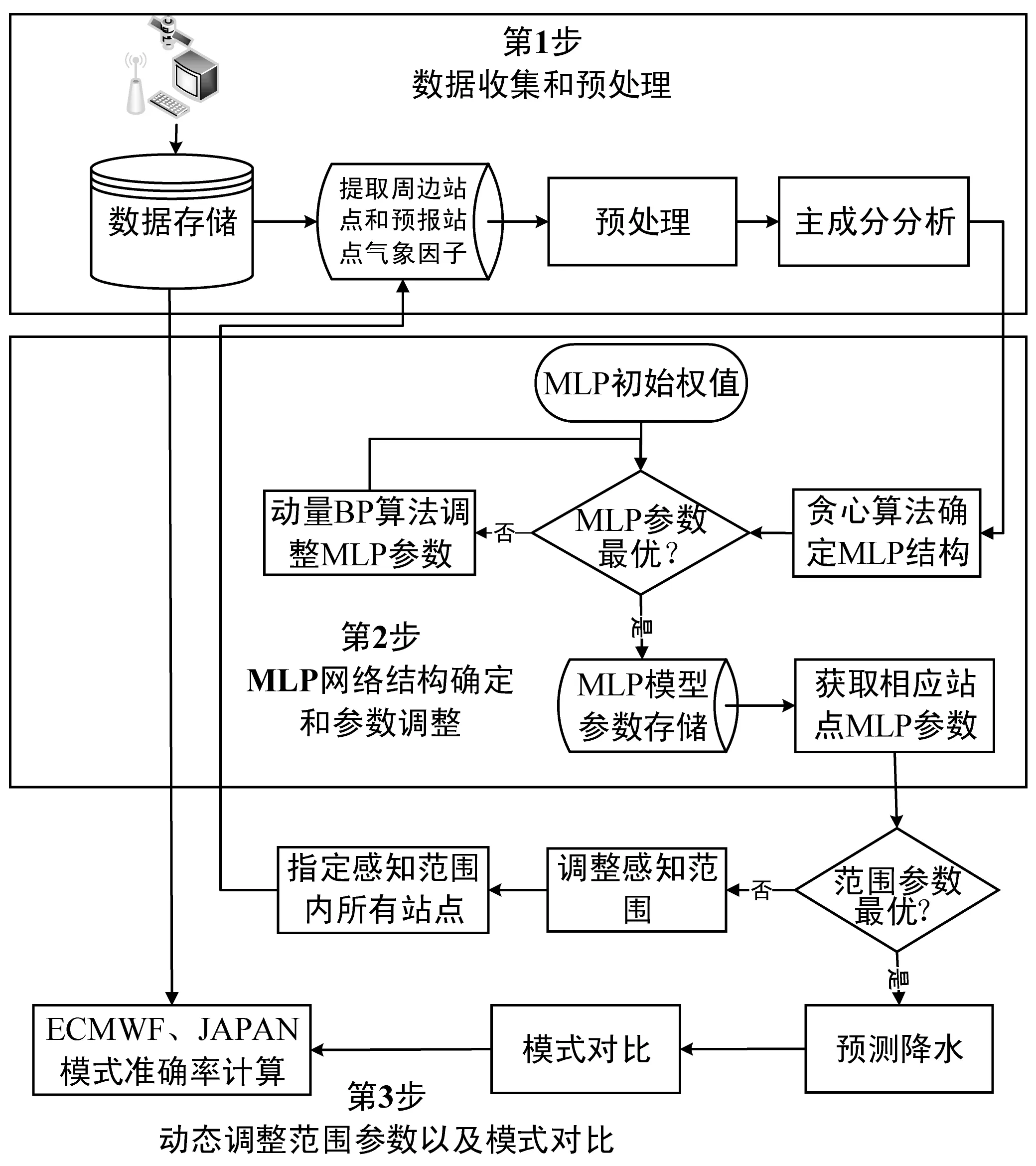
图2 DRCP建立过程
2.1 数据收集和预处理
数据收集主要收集13个气象因子,具体因子如表1所示。其中地面因子需要收集预报(中心)站点和周边站点的差值,其余因子为预报站点的值。

表1 MLP训练过程输入和输出气象因子
数据预处理包括离差标准化和主成分分析。由于各因子的量级不同,通过离差标准化方法将数据标准化到[0,1]之间,离差标准化的计算方法如下:
(7)
式中:x表示原变量序列中的某个值;xmax和xmin分别为变量中的最大值和最小值。
PCA可以在尽多保留因子整体信息的前提下,将因子的数目缩减,节省软硬件资源,PCA保留信息的标准为99%,此时新因子数据一般在6个以下。
2.2 MLP网络结构确定和参数调整
DRCF模型在中心地区和每一个周边地区之间建立联系,通过MLP来学习这种联系,此时每一个周边地区都可以预测中心地区的降雨,但这种准确率较低。为了提高预报准确率,使用多个周边地区(即MLP)一起预测中心地区的降水。DRCF的第二步是建立周边地区与中心地区的MLP,存储MLP权值和偏置,用于后期的预测。MLP的确定包括两个阶段:结构选择阶段和权值训练阶段。权值训练阶段的计算方式如1.2节所示。结构选择阶段采用贪心算法,即逐层确定每层结点个数,逐层顺序有两种:从输入层到输出层和从输出层到输入层。判断MLP优劣的标准是该MLP用于预测的均方根误差RMSE,其计算方法如下:
(8)
式中:N表示样本个数;y实况和y预测分别表示每个样本实况降水量和预测降水量。
2.3 动态调整范围参数以及模式对比
DRCF通过多个周边站点(MLP)共同预测中心站点的降水。当这些MLP中出现预报值大于0时,则预报有降水,且降水量等于它们的平均值;如果这些MLP中均预报无降水,则预报无降水。MLP的个数会影响预测的准确率,为了让DRCF达到最优的预测效果,MLP的个数是重要的研究对象。由于不同地区气象站点的分布密度不同,单独以MLP的个数作为一致的标准并不准确,DRCF模型以距离中心站点的距离作为标准选择周边站点,即选择某个距离内的所有周边站点,这个距离成为感知半径。感知半径代表着感知范围的大小,是感知范围的参数。两个站点之间的距离定义如下:
(9)
式中:x1和y1分别为预报中心站点的经度和纬度;x2和y2分别为周边站点的经度和纬度。
由于降水系统的空间特性,在预报过程中保持感知范围不变,并不一定达到最佳效果。在预报过程中动态调整感知半径,即动态调整MLP的个数,称这个过程为动态感知。图3展示了这种动态感知过程,中间较大圆圈表示预报站点,其余较小圆圈表示周围站点,实线表示周围站点与预报站点的联系,不同的虚线圈表示不同的感知范围。

图3 DRCF的感知过程
模式对比阶段,将DRCF的预报准确率和ECMWF及JMA数值模式做对比。准确率的计算标准除了RMSE外,同时采用TS评分,TS评分是目前中国气象业务中最常用的预报评价标准之一。TS评分方法中预报晴雨准确率(R)、预报降水准确率(r)和综合准确率(C)的计算方法如下:
(10)
(11)
(12)
式中:N1表示预报降水正确的样本数;N2表示预报无降水正确的样本数;N3表示预报没有降水但实际出现降水的样本数;N4表示预报有降水但实际没有出现降水的样本数。
3 实验与结果分析
3.1 实验环境与数据
实验所用设备软硬件配置如下,CPU:Lenovo Intel Core i3-2330M,内存:8 GB,硬盘:256 GB,操作系统:Windows 7。实验计算的软件使用MATLAB 2013a,DRCF模型中计算PCA时,使用MATLAB自带的princomp函数,MLP的动量BP调整算法使用MATLAB自带的learngdm权值学习函数,并通过train函数判定MLP训练结束。
实验使用的数据包括中国气象局发布的2015年-2017年地面填图数据和高空(500 hpa)填图数据,时间精度为3小时,两种数据均是按照气象站点排列的文本数据,可以按照地区编号提取数据。比较DRCF准确率时使用ECMWF和JMA数值模式2017年发布的逐3小时降水预报数据。这种数据是按照经纬度排列的格点式文本数据,可以根据经纬度提取相应地区的降水预报值。实验选择了全国56个地区(站点)作为预报对象,这56个地区均具有地面气象观测站和雷达探空站。DRCF模型需要一个预报中心地区和数个周边地区,周边地区选择中心地区周边的普通站点。图4中圆点表示56个中心站点的分布。
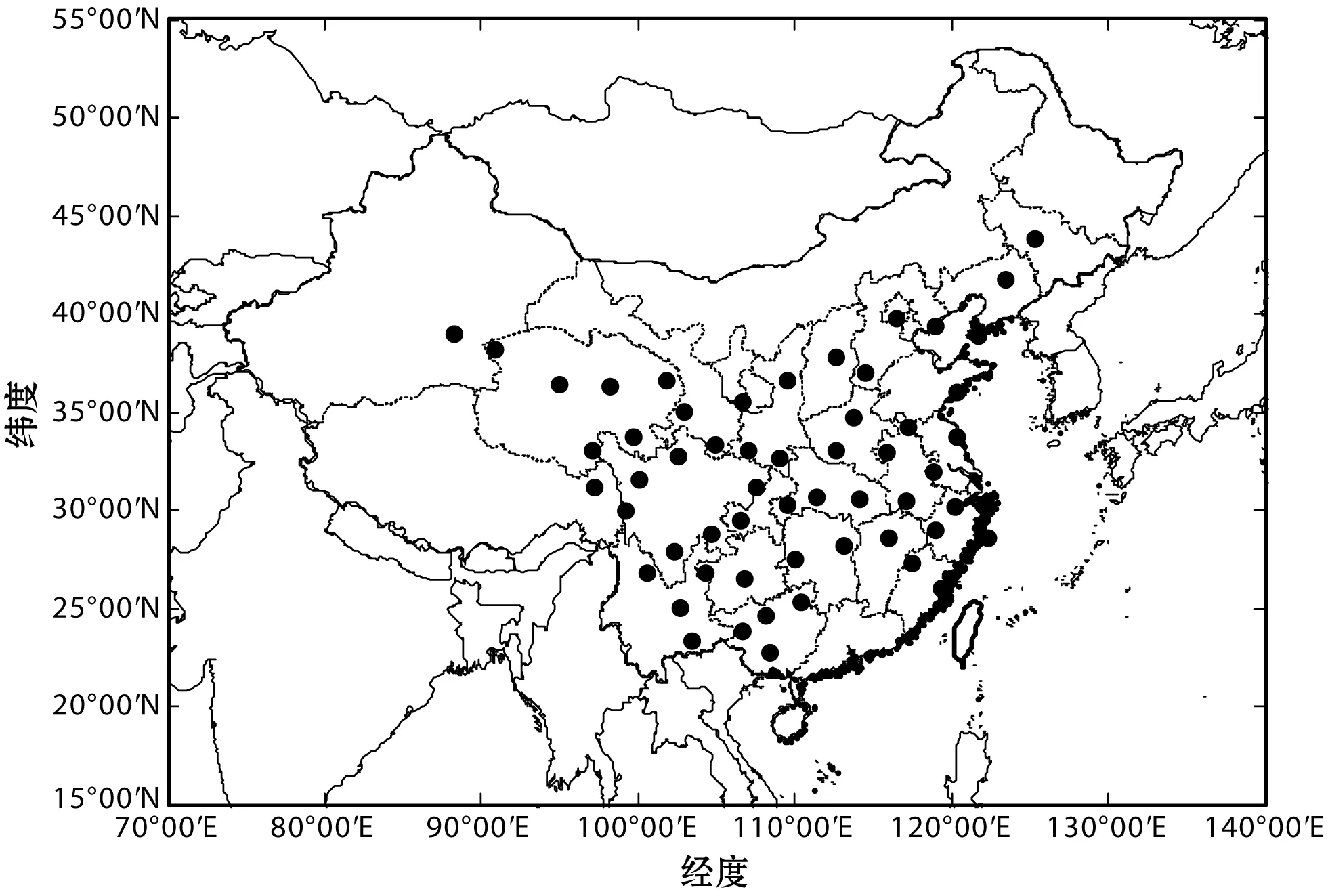
图4 中心站点分布
3.2 感知范围参数和准确率变化
不同的感知范围确定不同的MLP个数,MLP个数不同,预报准确率将不同。由于气象站点分布密度的差别,DRCF中使用感知半径来决定MLP的个数。为了说明这种策略的合理性,实验通过概率分布的方式比较分别用MLP个数和感知半径来确定最优值的区别。实验分别统计56个站点达到最高综合准确率时的MLP个数和感知半径的概率分布情况。图5中,(a)和(b)分别表示最优感知站点(MLP)个数和最优感知半径的概率分布。对比发现,最优感知半径的分布更为集中,而最优MLP个数却较为分散。对于56个预报站点,无法选择一个合适的最优MLP个数,但可以选择一个合适的最优感知半径。因此选择感知半径作为范围参数是合理的选择。
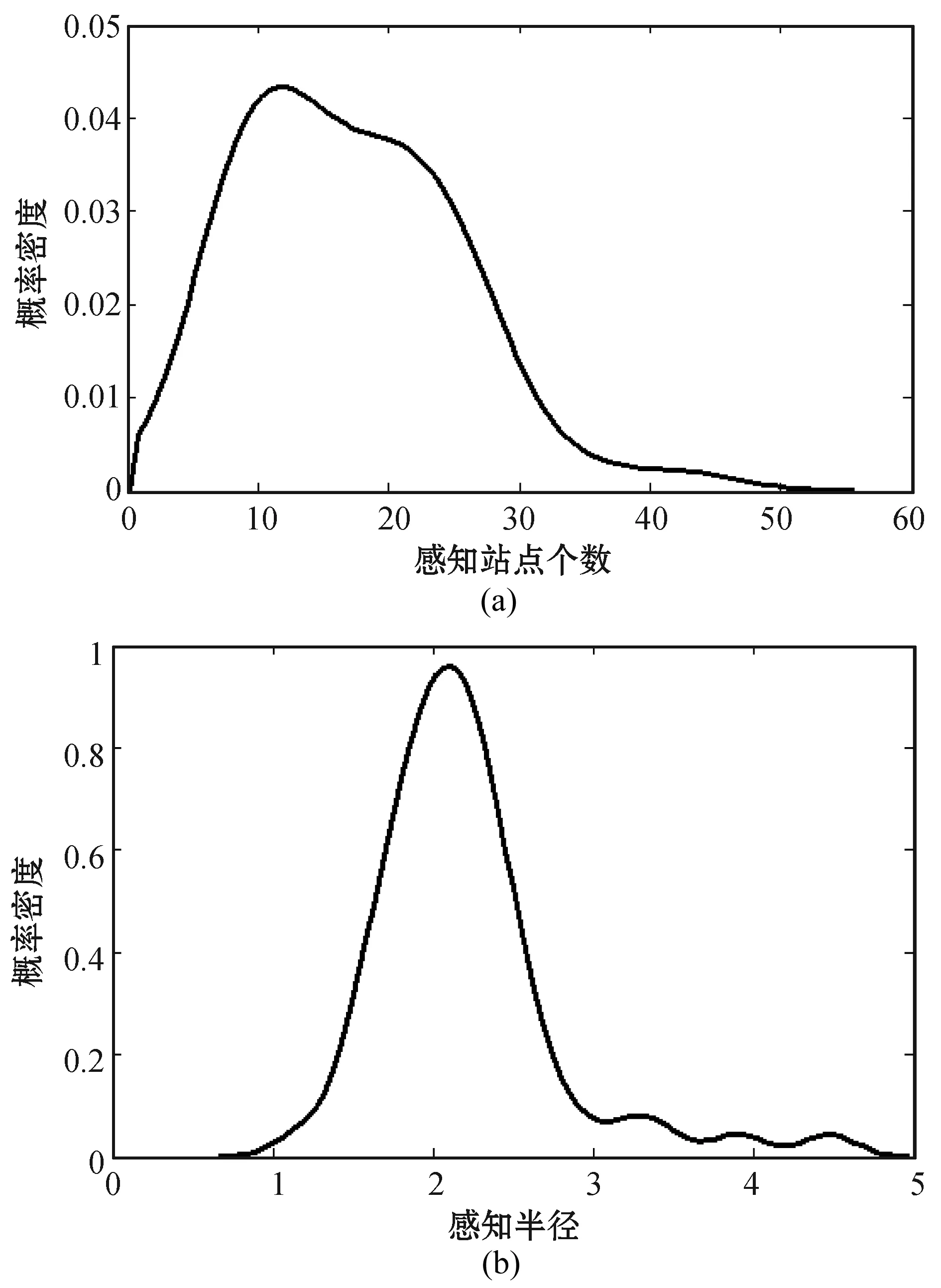
图5 最优感知站点个数和最优感知半径的概率密度分布
从图5(b)可以看出,56个站点中大多数站点当感知半径约等于2时,综合准确率达到最大。为了更准确地说明感知半径对准确率的影响,图6表示56个站点的4种准确率平均值随感知半径的变化情况。可以发现,随着感知半径的增加,预报晴雨准确率逐渐减小,预报降水准确率逐渐增加,综合准确率在2附近达到最优,RMSE在2~3.5之间达到最优。综合考虑四种准确率,当感知半径为2时,预报能力最佳。
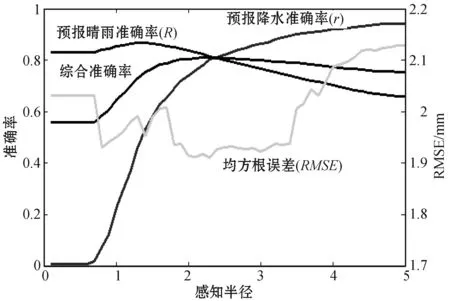
图6 准确率随感知半径的变化情况
3.3 动态感知和数值模式对比
当感知半径越大,预报降水命中率增加,而预报晴雨准确率下降,原因是随着感知范围的扩大,新增的周边站点某些时候会对预报站点做出错误判断,干扰了预报。分析两种准确率的定义可以发现,错误预报包括两种情况:(1) 预报站点有降水却没有预报出来,此时说明降水范围较大,感知范围过小;(2) 中心站点没有降水却误报降水的情况,说明降水在其余地区,没有影响到本地,此时感知范围过大。为了减小这两类错误的发生,提出改进措施,在预报站点出现降水时,增加感知范围,而在没有降水的情况下减小感知范围。由3.2节知最优感知半径为2,因此设置感知半径的波动范围为1.5~2.5之间,动态感知策略调整感知半径以及计算预报结果的算法过程如下:
定义station和station_0表示站点对象,其中station_0表示预报中心站点对象,station_0.rain表示预报站点的降水序列;station表示某个周边站点,station.rain表示周边站点的降水序列,station.MLP表示周边站点MLP的预测结果,staion.range表示周边站点到预报站点的距离。radius表示感知半径。station_1表示周边站点集,station_2表示感知半径内周边站点集。
(1) 确定感知半径radius。
if station_0.rain[t-1,t-2,t-3]=0 && all station.rain[t-1]=0
radius←1.5
else if station_0[t-1,t-2,t-3]=0 && some station.rain[t-1]>0
radius←2.5
else if station_0[t-1]>0
radius←1.5
else
radius←2
end
(2) 寻找radius内周边站点,加入station_2集。
for station in station_1
if station.range add station to station_2 end end (3) 计算预报值rain。 rain←0 number←0 for station in station_2 if station.MLP>0 rain←rain+station.MLP number←number+1 end end if number>1 rain←rain/number else rain←0 end 动态感知策略是DRCF的重要组成部分,为了说明模型的预报性能以及动态调整策略的合理性,将未使用动态调整策略的模型(感知半径保持为2,记为RCF)、使用动态调整策略的模型(DRCF)以及ECWMF、JMA数值模式分别应用于56个气象站点,计算R、r和RMSE三种准确率的平均值,分别记为R平均、r平均和RMSE平均,结果如表2所示。 表2 DRCF与ECMWF、JMA数值模式准确率对比 对比发现,与RCF相比,R平均、r平均分别提高了0.02和0.03,而RMSE平均减小了1.09,预报性能有所提高,因此动态调整策略可以提高预报准确率。与两家数值模式对比,DRCF在三种准确率上均优于两家数值模式。 当前基于DL的降水预报方法,通常以某一地区的物理量和降水分别作为网络的输入和输出,没有考虑到不同地区之间的联系和降水系统的空间性质。本文在预报站点和周围站点之间建立联系。通过PCA方法对大气环流背景场和局地气象要素差异等13个因子降维,并在预报中心地区与每个周边地区之间建立MLP,学习相邻站点之间的降水联系。通过多个MLP同时预报中心地区的降水,并动态改变MLP的个数,建立了DRCF模型。实验证明,感知半径的不同导致DRCF的准确率不同,当感知半径为2时,DRCF的综合准确率最高。动态调整感知半径可以提高DRCF的准确率,DRCF可以有效预报3小时降雨量,预报准确率高于ECMWF和JMA数值模式。然而,DRCF的预报时效为3小时,而实际业务中往往需要更长的预报时效。因此,下一步将会在预报时效上提出改进措施。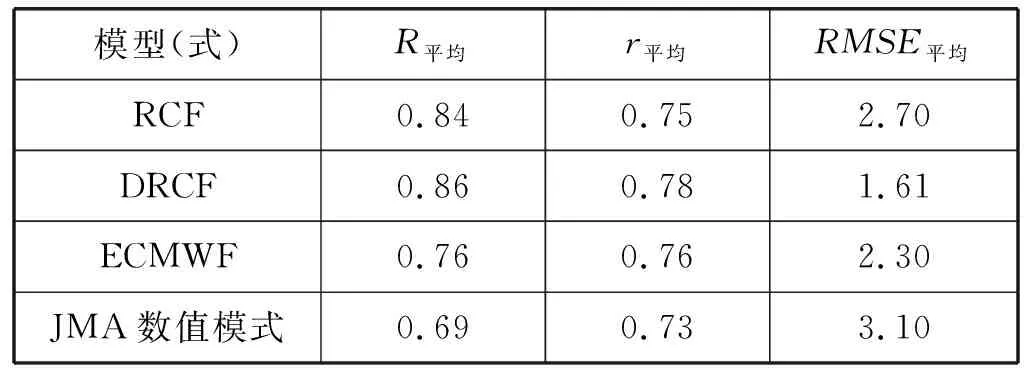
4 结 语

