基于改进的PSO算法优化FSVM的滚动轴承故障诊断
林雅慧 王海瑞 靖婉婷
(昆明理工大学信息工程与自动化学院 云南 昆明 650500)
0 引 言
捣固车是一种大型养护机械,其主要用于铁路新路线的施工和铁路维护时的故障清除等,目的是为了保障列车可以稳定高效的运行。因此,对捣固车的各种故障进行快速准确地判断具有不可忽视的工程价值[1]。滚动轴承是机械设备的重要组成部分,也是故障频发的部件之一,它以很大概率决定着整个机械设备能否正常工作[2]。由于传统的依靠个人经验进行故障诊断不仅浪费了大量的时间和精力,而且其诊断精度往往不高。
由Vapnik等在1995年提出的新型分类器支持向量机SVM,一经提出便受到海内外学者的广泛关注[3-5]。SVM主要用于线性分类问题,通过构造一个最优超平面把问题进行分类;而那些线性不可分的问题主要是通过核函数把低维空间映射到高维空间中去,从而实现线性可分[6-8]。虽然SVM具有较好的分类能力和全局泛化能力,但因为受到环境因素的影响,SVM所采集的样本有噪声点和孤立点等模糊信息的存在,最终造成分类无法实现群体最优,诊断准确率也大幅度降低。为了解决这一问题,在2002年Lin等[9]提出了模糊支持向量机FSVM的概念,将模糊因子引入支持向量机中,有效地改善了外界因素对分类精度的影响。鉴于FSVM良好的分类性能,本文选取FSVM作为滚动轴承的故障检测方法。
粒子群算法(PSO)具有结构简洁,运算中无需过多的参数调节,实现速度快,轻松与其他方法相融合等优势。因此,本文选取粒子群算法用于FSVM模型的优化。同时为了更大限度地均衡粒子群优化算法模型的全局寻优优势和局部寻优优势,本文将在算法寻优的过程中加入惯性因子。融入了动态更新惯性权重的IPSO-FSVM分类模型大大提高了分类的精度和效率。通过对比实验可以看出,本文所提出的故障诊断模型在性能和时间等各个方面都优于其他故障诊断模型,验证了本文所提方法的优越性。
1 粒子群优化算法及其改进
1.1 基本粒子群优化算法
美国Kennedy和Eberhart博士在1995年提出一种启发式随机优化的全局优化算法,即粒子群优化算法PSO[10]。该算法主要是通过观察研究鸟类的觅食行为并结合Ryunolds和Heppner的两位生物学家所提出的两种鸟群模型来优化问题[11-14]。在粒子群优化算法中,位置和速度两个向量尤为重要。假设粒子的搜索空间为N维空间,种群粒子总数为M。第i个粒子在第t次寻优时,其位置表示为Xi(t)=[Xi,1(t),Xi,2(t),…,Xi,N(t)],速度表示为Vi(t)=[Vi,1(t),Vi,2(t),…,Vi,N(t)],粒子的个体极值表示为Pi(t)=[Pi,1(t),Pi,2(t),…,Pi,N(t)],全局极值表示为G(t)=Pg(t)=[Pg,1(t),Pg,2(t),…,Pg,N(t)],1≤g≤M。采用式(1)进行粒子的个体极值更新:
(1)
对(t+1)时刻粒子群算法的粒子速度和位置进行更新:
Vi,j(t+1)=Vi,j(t)+c1·r1,i,j(t)·(Pi,j(t)-
Xi,j(t))+c2·r2,i,j(t)·(Gj(t)-Xi,j(t))
(2)
Xi,j(t+1)=Vi,j(t+1)+Xi,j(t)
(3)
式中:1≤i≤M,1≤j≤N;t表示的是粒子进行第t次寻优;c1和c2均为常数,表示学习因子,c1用来保证粒子向局部最优位置移动的距离,c2用来保证粒子向全局最优位置移动的距离;r1,i,j(t)和r2,i,j(t)~U(0,1)。
1.2 改进的粒子群优化算法
为了很好地平衡粒子群优化算法的全局寻优能力和局部寻优能力,本文引入惯性因子ω来达到上述目的。在式(2)中加入惯性因子ω后,其速度更新公式改为:
Vi,j(t+1)=ωVi,j(t)+c1·r1,i,j(t)·(Pi,j(t)-Xi,j(t))+
c2·r2,i,j(t)·(Gj(t)-Xi,j(t))
(4)
一般情况下,学习因子的大小严重影响到群体的收敛速度,设c1=c2=2。
在粒子群优化算法中为了避免信息丢失,尽可能地实现全局寻优最优化。在对速度进行更新调整时,可引入交叉变异思想,进而在某些方面改进了全局搜索极值的能力。为了使得粒子惯性权重ω的调节更为合理,本文在确保ω拥有明显的自适应特征的同时,将适应度函数的结果融入到粒子惯性权重ω的调节流程中。粒子惯性权重ω如下:
(5)
式中:ωmin、ωmax分别表示惯性因子的最小值和最大值。根据以往的实验经验,可取ωmin=0.3、ωmax=1.0。
当f≥favg时,f与favg接近,惯性因子ω相应地增加,f与favg远离,惯性因子ω相应地减少,使得粒子不再局限于局部最佳,而向全局最优靠拢,突显了收敛性的特质;当f 假设模糊支持向量机的训练集为:S={(x1,y1,μ1),(x2,y2,μ2),…,(xl,yl,μl)}。其中:xi∈Rn;0<μi≤1;yi∈{-1,1},i=1,2,…,l;μi模糊隶属度表示样本xi属于某类的程度。松弛变量ζi用来检测样本分类的误差,μiζi表示样本中含有模糊问题的松弛变量,用来降低重要性不同的变量被错分的可能性。模糊支持向量机的最优分类超平面如下: (6) s.t.yi(ω·φ(xi)+b)-1+ζi≥0 (7) 式中:ζi≥0;惩罚系数C为常数,FSVM方法对惩罚系数C进行模糊化处理,确保了不同的隶属度在模型中发挥不一样的作用。当样本取得一个较小的隶属度值时,将减轻样本对整体的作用,同时也降低了外界模糊信息对FSVM的影响。 本文的目的是解决适用于轴承故障诊断的多值分类器的设计问题。多类分类方法可分解成多组两类分类方法,并将两类分类方法使用二叉树的结构结合而成进行分类使用。本文使用改进的自适应ω惯性因子对IPSO-FSVM模型参数进行改进优化,使得所构造的N类故障分类器为性能最优。其模型如图1所示。 图1 基于改进的PSO的多分类FSVM故障检测模型 为了佐证改进的粒子群算法优化FSVM故障诊断模型性能良好,本文选用美国凯斯西储大学(Case Western Reserve University)提供的相关数据进行实验[15]。实验根据小波三层分解原理,提取轴承的能量特征,其部分实验数据如表1所示。实验选取轴承的4种状态(正常、内圈故障、外圈故障和滚动体故障)[16],每种故障选取30组样本作为训练样本,总共需要选取120个特征向量,并将选取的120组特征向量录入到数据样本中为训练做准备。对每种故障选取20个特征向量,共80个存入到数据样本中作为测试样本集。实验设置惩罚系数C=[0.01,100],径向基核函数参数σ=[0.05,100],迭代次数为200次。 表1 小波提取轴承故障能量特征的部分样本 为了体现文中方法的优势,实验将对改进的粒子群优化算法优化FSVM和基本的粒子群优化算法优化FSVM在轴承中的故障样本进行比较训练,其中包括寻优的效率和检测的准确率,从而判断改进的粒子群优化模糊支持向量机的鲁棒性。实验通过对比上述两种故障诊断模型的迭代次数与适应度函数值,其关系如图2所示。 图2 PSO-FSVM和IPSO-FSVM的迭代次数与适应度的关系图 本文选取相对误差作为两种模型的适应度函数值。适应度函数值收敛时,意味着FSVM模型取到最优参数,也就说明其预测相对误差最小。从图2中可以看出,当改进的粒子群优化算法参数达到最优时,算法迭代到第42次;当基本的粒子群优化算法参数达到最优时,算法迭代到底69次,此时惩罚系数C和核函数参数σ取到最优解,但不如IPSO。因此,可以得出,IPSO对FSVM参数寻优速度比基本的PSO对FSVM参数寻优速度快,并且判断错误率较低。 为了证明IPSO-FSVM模型的优越性,设置对比实验。在两种模型的训练数据和测试数据都相同的情况下进行故障类型的识别,通过实验结果来证实IPSO-FSVM诊断模型的鲁棒性。图3和图4为两种故障诊断模型的预测测试集分类结果。 图3 PSO-FSVM预测与实际分类比较 图4 IPSO-FSVM预测与实际分类比较 表2更为直观地表述了两种故障诊断模型的诊断正确率。 表2 IPSO-FSVM和 PSO-FSVM故障诊断模型的诊断正确率 由图3、图4和表2可知,当采用PSO-FSVM模型进行故障诊断时,其诊断正确率为90.00%;当采用IPSO-FSVM模型进行故障诊断时,其诊断正确率高达93.75%,已经能够较好地对轴承的各类故障进行识别分类。由实验结果可知,对于小样本集,使用IPSO-FSVM模型得到的分类准确率比PSO-FSVM来的高,说明IPSO-FSVM模型的分类能力很强,能够高效地完成小样本的故障检测。 本文根据小波三层分解对故障信号进行能量特征提取,将分解所获得的各频段信息重构,最终提取能量特征输入FSVM模型,完成模型的训练。采用基于模糊样本点的FSVM方法进行轴承故障分类,有效地解决了噪声及模糊点对分类结果的影响。同时为了提高分类效率,选取粒子群优化算法优化FSVM参数,并将粒子群优化算法进行改进,融合惯性因子从而更大限度地均衡粒子群优化算法模型的全局寻优优势和局部寻优优势。 实验结果表明:改进的粒子群优化算法对FSVM参数寻优速度比基本的粒子群优化算法对FSVM参数寻优速度快,分类效果好,很大程度上提高了轴承故障分类的效率以及准确度,拥有很好应用价值。2 模糊支持向量机及其改进算法
2.1 模糊支持向量机
2.2 改进粒子群算法优化模糊支持向量机
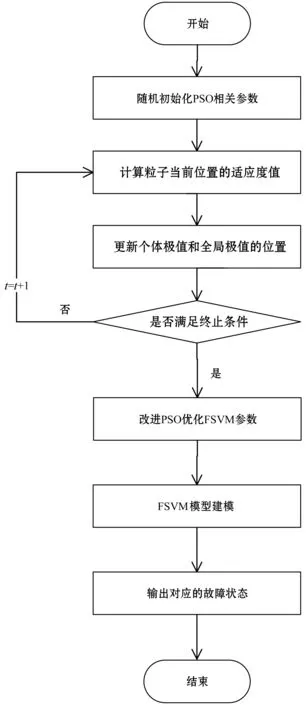
3 实验及结果分析
3.1 实验准备和特征提取

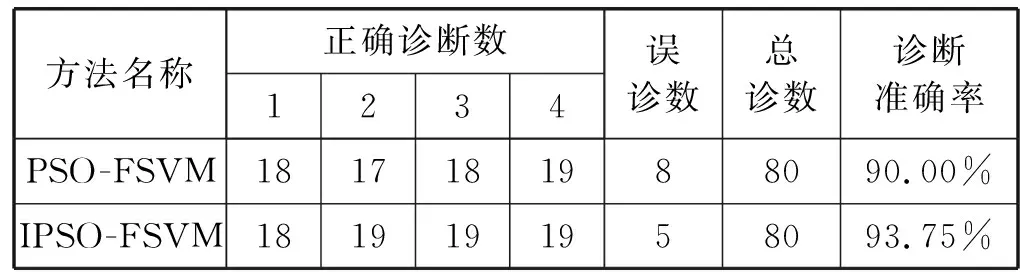
3.2 实验结果分析



4 结 语

