空隙率对钢筋石笼拖曳系数的影响研究

伍学文，郭红民，张田甜，张 杨，柳 滔，胡海松

(1.三峡大学水利与环境学院，湖北 宜昌，443002；2.中国葛洲坝集团基础工程有限公司，湖北 宜昌，443002)

块体在水流作用下的稳定性与水平方向的拖曳力直接相关，在拖曳力的表达中拖曳力系数的确定是非常重要的。杨文俊[1]指出对于立方体截流材料的推力系数(包括拖曳系数和上举力系数)一般选取1.1，四面体和块石一般选取0.6～1.1；叶恩立[2]认为拖曳系数是关于形状的函数，研究得到不同形状所对应的拖曳力系数值；毛伟[3]将块体形状概化为长方体，研究了在此形式下的拖曳力与块体形状的关系式。目前多是针对未考虑空隙的块体进行的研究，但钢筋石笼因有空隙具有透水性的特点导致其在水流中的稳定情况与块体存在不同。针对有空隙的钢筋石笼的研究，郭红民[4]等从钢筋石笼的空隙率出发对综合稳定系数做过相关研究，得出空隙率越大，综合稳定系数越大的结论。但对于带有空隙的钢筋石笼在计算拖曳力时，拖曳系数的确定相关研究资料较少。本文将探讨空隙率对钢筋石笼的拖曳系数的影响，为实际工程应用提供参考。

1 理论分析

钢筋石笼在水流作用下主要受5个力的作用：拖曳力FD、上举力FL、重力G、浮力Ff和阻力FZ。其受力分析如图1所示。水流流动导致钢筋石笼与水流发生相对运动，从而会产生拖曳力FD；钢筋石笼在水流中，由于顶部和底部流速不相等，根据伯努利方程会产生压力差，产生上举力。引用Eveet[5]等人关于拖曳力和上举力的计算公式如式(1)和式(2)，其中CD为拖曳系数，CL为上举力系数，A1为迎水面面积；A2为底面面积，v为块体起动流速，γs为钢筋石笼容重，γ为水的容重，μ为底面摩擦系数，V为钢筋石笼体积。其中CD和CL不是常数，随块体的形状、雷诺数、攻角以及透水性等的不同而不同，这些因素相互影响。对于他们之间的变化规律仅有一些经验性的公式和成果，没有成熟的计算公式。尤其是针对有空隙的钢筋石笼，限于试验条件和测试手段，用传统试验方法和理论分析难以直接得其与空隙率之间的关系。所以本文将借助数值模拟的方法对其进行研究。

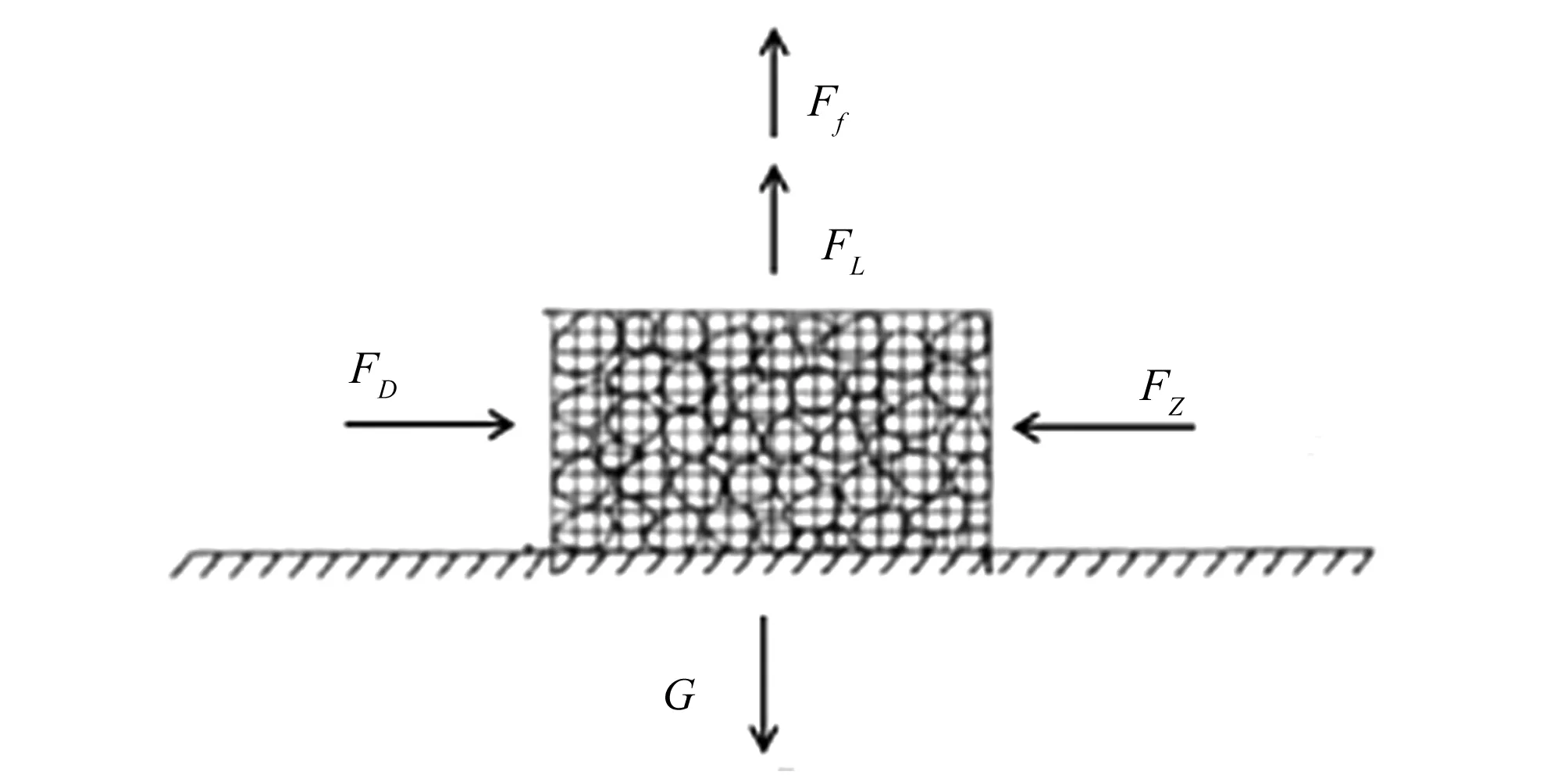
图1 钢筋石笼受力图Fig.1 Force diagram of reinforced gabion

(1)

(2)

Ff=ρgV

(3)

FZ=μ(mg-FL-Ff)

(4)

2 数学模型的建立2.1 控制方程

连续方程：

(5)

动量方程：

(6)

式中：ρ为体积分数平均的密度；μ为分子黏性系数；р为压强；μt为紊流黏性系数，其表达式为 ，其中Cμ为经验常数,Cμ=0.084 5；μ+μt为广义黏性系数；μi，μj分别为流速矢量在xi，xj方向的分量。

2.2 紊流模型

RNGk-ε模型在经过了改进和实用化的处理后，在形式上类似于标准k-ε模型，但是在计算功能上强于标准k-ε模型，其考虑了旋转效应，因此对强旋转流动计算精度也较高，模型中包含了计算湍流Prandtl数的解析公式，并且对近壁区进行适当处理后可以计算低雷诺数效应。经过许多学者的验证表明RNGk-ε对复杂水流形态模拟精准。

紊动能k方程：

(7)

紊动耗散率e方程：

(8)

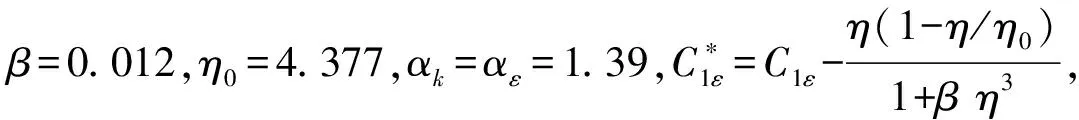
2.3 拖曳力及拖曳系数的计算

FD=Fpress+Ffric

(9)

(10)

(11)

(12)

结合数值模拟可提取的数据，根据式(12)可以得到在本文计算条件下，不同空隙率所对应的拖曳力系数CD如表1所示。

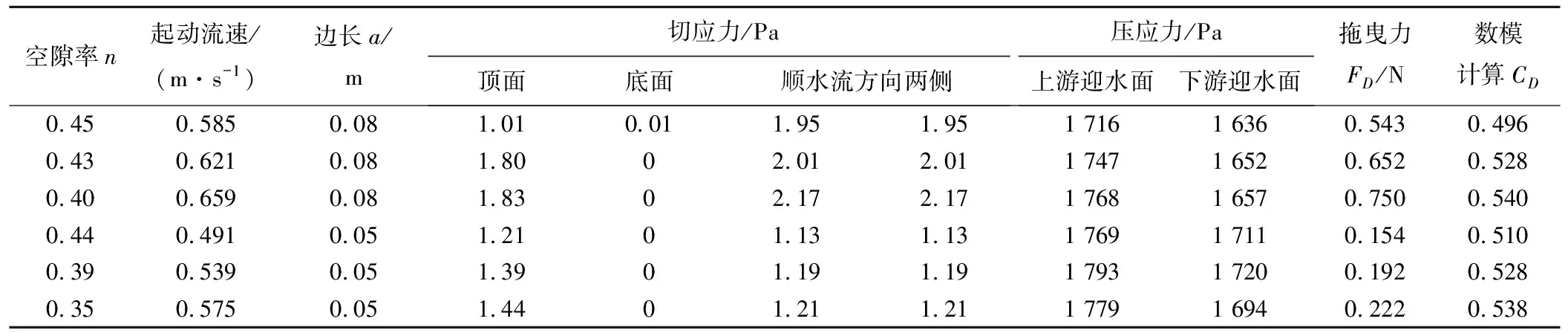
表1 数模计算钢筋石笼不同空隙率对应的CD值Tab.1 Calculation of CD value corresponding to different voids in reinforced gabion by numerical simulation

3 试验及数模验证

庞启秀[6]在研究块体在水流作用下的试验时指出对于非球形颗粒，每个颗粒虽有不为0的升力，但颗粒群中由于各颗粒取向的随机性，这些力互相抵消，因此通常不考虑上举力，并在其试验中得到了验证；Zhu[7]研究表明上举力数值很小接近零；叶恩立、周宜红[2]等对钢筋石笼研究时指出，由于钢筋石笼的透水性，在其底部面积不大时，上举力的影响远小于拖曳力对稳定性的影响。根据上述已有的研究成果，忽略上举力的影响，根据前面的理论分析，由式(1)、式(2)、式(3)和式(4)可以得到起动流速公式如式(13)所示，流速和拖曳系数以及钢筋石笼空隙率有关。根据公式(13)得到通过试验计算的拖曳系数公式(14)。

(13)

(14)

本文设计制作了两种尺寸大小、三种不同空隙率的正六面体钢筋石笼在水槽中进行了试验研究，水槽底面摩擦系数为μ=0.21，如图2所示。在钢筋石笼开始滑动条件下测得的流速作为不同尺寸大小不同空隙率的钢筋石笼的起动流速如表2所示。

图2 不同空隙率的钢筋笼模型Fig.2 Reinforced gabion model with different voids

将试验所得起动流速值带入式(14)得到相应的拖曳力系数见表2。为了验证数值模拟计算的准确性，将数模计算结果同物理模型试验结果进行对比如表2所示。由表2可知数值计算得到的拖曳系数与试验实测数据计算得到的结果较为接近，两者最大偏差率不超过1.32%，表明数学模型具有较好的计算精度；同时在忽略上举力的影响得到的公式(13)具有一定的适用性。

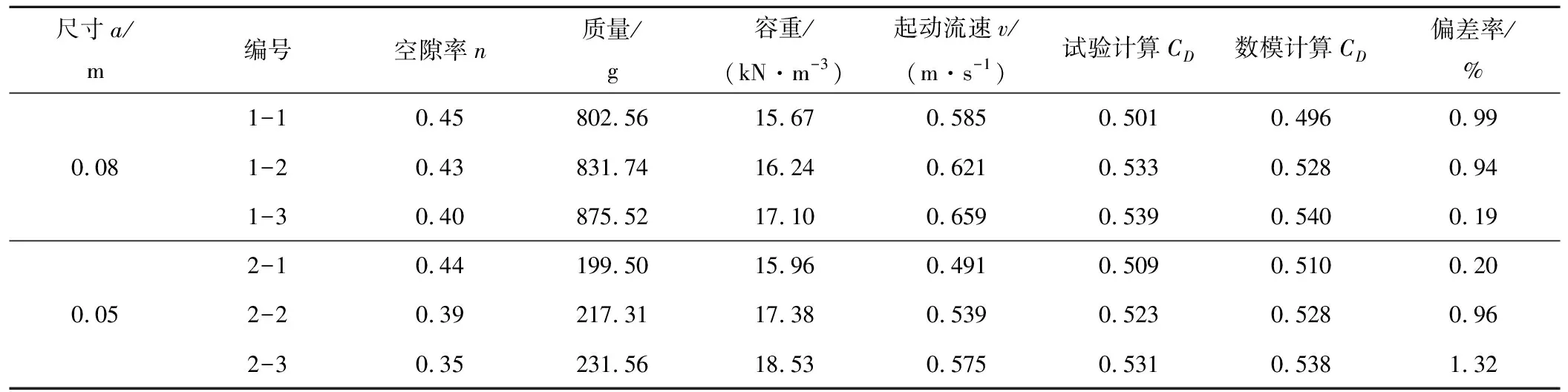
表2 两种尺寸不同空隙率钢筋石笼起动流速及CD值Tab.2 CD value and starting velocity of reinforced gabion with two sizes and different voids

4 空隙率与拖曳系数关系的拟合

为了进一步探讨空隙率和拖曳力系数之间的关系，本文对钢筋石笼在尺寸大小及摩擦系数相同的情况下，采用数值模拟探讨了在不同流速与不同空隙率下的钢筋石笼的拖曳力系数CD的变化。设置正六面体钢筋石笼模型边长为0.08 m，摩擦系数为0.48(模型在光滑水泥面上实测值)，在同一流速下设置5种不同的空隙率，共设置五组流速做参照对比试验。根据式(9)、式(10)、式(11)和式(12)，给定边长，摩擦系数和流速设置单一变量空隙率，根据数值模拟提取结果计算出拖曳力FD，再计算拖曳力系数CD，数值模拟提取值如表3所示。不同起动流速下的钢筋石笼空隙率与拖曳力系数CD关系曲线图如图3所示。

从图3知，在钢筋石笼尺寸、摩擦系数以及给定流速相同的情况下，空隙率会对拖曳力系数CD产生影响，并且随着空隙率的增大，拖曳系数减小，钢筋石笼所受拖曳力越小，越稳定。与前人研究得到的空隙率越大，钢筋石笼的综合稳定系数越大的结果相符。

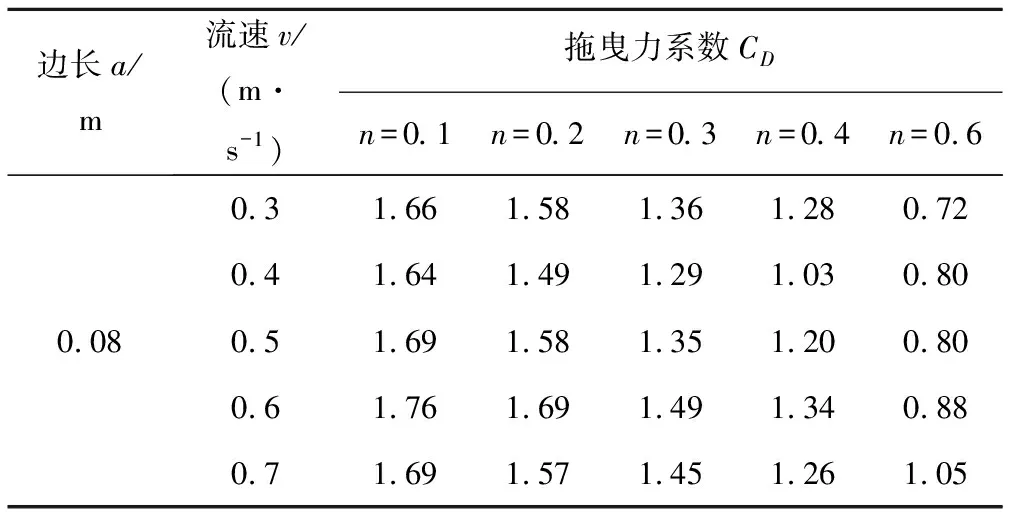
表3 钢筋石笼空隙率与拖曳力系数关系表Tab.3 Table of relationship between void ratio and drag force coefficient of reinforced gabion

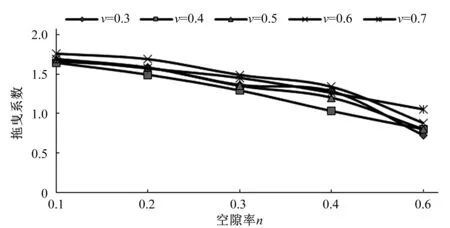
图3 钢筋石笼不同流速下的空隙率与拖曳系数的关系曲线Fig.3 The relationship between void ratio and drag coefficient of reinforced gabion under different Velocity

将表3与图3得到的结果通过拟合得出空隙率与拖曳力系数CD的关系式如式(15)。将式(15)带入式(13)得到新公式如式(16)。

CD=0.9n-0.3

(15)

(16)

5 拟合公式的验证

根据修正后的起动流速公式(16)计算得到的流速与通过模型试验得到的起动流速对比，对比结果如表4所示，对比图如图4所示。由对比结果可知，最大偏差不超过1.97%，说明修正公式(16)计算得到的流速值与试验所得的起动流速值基本吻合。由此可见，拖曳力系数与空隙率的关系式有一定的准确性，经过修正后的起动流速公式可用于正六面体钢筋石笼的抗冲稳定计算。

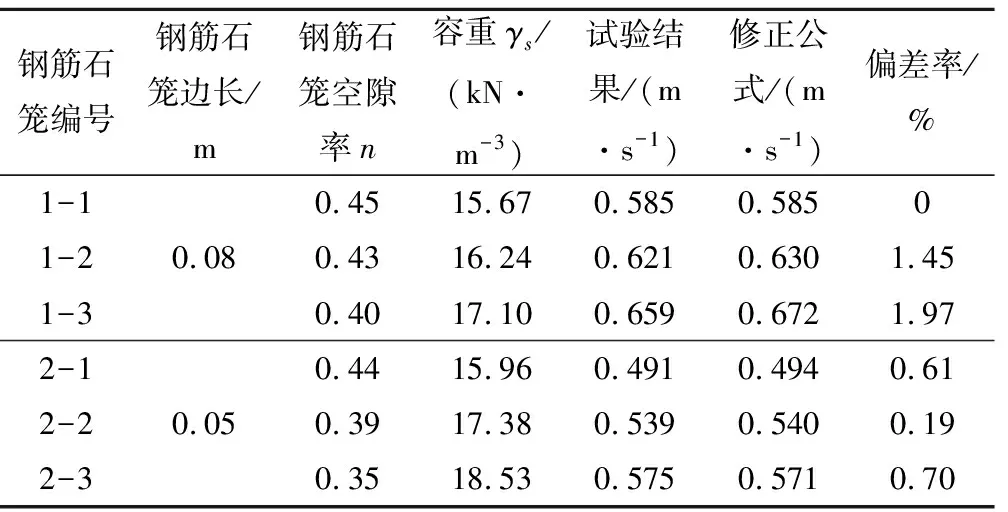
表4 钢筋石笼起动流速对比Tab.4 Comparative Diagram of starting Velocity of reinforced gabion

6 结 语

(1)通过模型试验和数值模拟结果对比，表明钢筋石笼空隙率n会对拖曳力系数CD产生影响，并随着空隙率的增大，拖曳系数减小，有利于钢筋石笼的稳定。

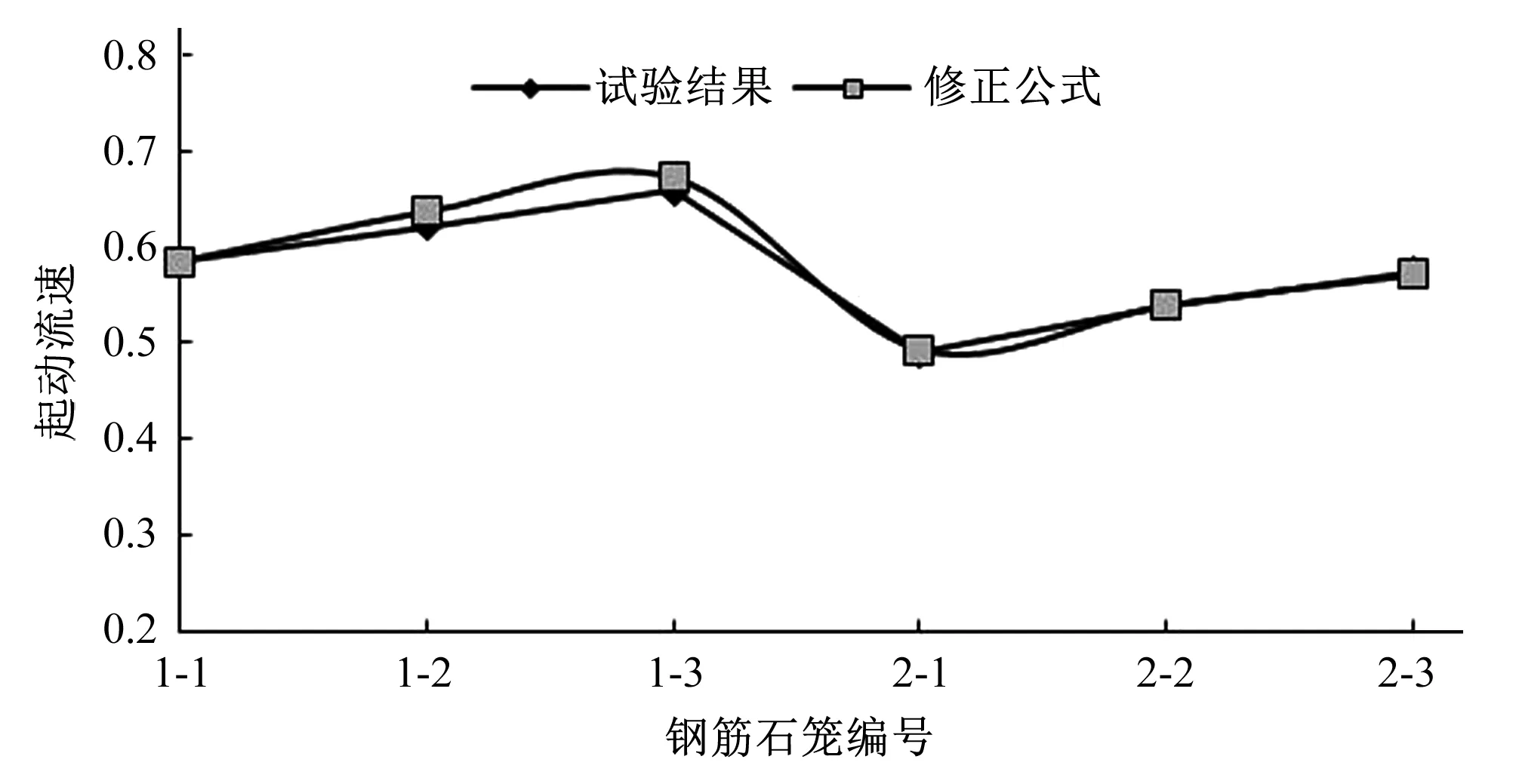
图4 试验结果与修正公式结果对比图Fig.4 Comparative diagram of test results and modified formula results

(2)通过拟合得到了空隙率n与拖曳系数CD的关系式，对正六面体钢筋石笼的起动流速公式进行了修正，通过与物理试验结果相比具有较好的吻合性。得到的空隙率与拖曳系数的公式可以为今后拖曳系数选取的参考依据，并且修正后的起动流速公式可用于正六面体钢筋石笼的抗冲稳定计算。

□