基于几何非线性的复合材料加筋壁板分析

刘智敏，孙启星 ，刘慧慧 ，毛端华 ，王艳丽，朱丽媛

（1.空军驻江西地区军事代表室，江西 南昌，330024;2.航空工业洪都，江西 南昌，330024）

0 引言

复合材料在航空领域应用日益广泛，在结构设计中经常采用加筋板、框梁等形式提高蒙皮薄板结构强刚度[1-3]，结构设计中一般采用线性分析即可满足设计要求，通过蔡吴准则或应变法判断结构是否安全[4]。非线性一般用于结构极限承载能力分析或结构损伤后剩余强度分析，以理论研究为主,在工程设计中，由于计算量大、设计参数多，非线性应用较少。

复合材料加筋壁板在充压分析时，采用线性计算不能与试验完全吻合，理论计算与试验强刚度结果差异较大。若对复合材料进行损伤演化分析，计算量比较大，且复合材料材料非线性段较短、试验数据不完善，计算精度会更差。基于复合材料以线性承载为主的特性，分析时可忽略材料非线性的影响，主要分析几何变形非线性对结构变形、承载的影响，计算结果仍采用蔡吴准则或应变法进行评估，即可满足计算精度要求，又可提高计算效率。

1 试验方法及结果

复合材料加筋壁板结构见图1，采用RTM工艺一次成型，结构充压时横筋承载大于纵筋，铺层设计纵筋在纵横筋交错时断开，方格内铺层按图2进行剪口铺层，其中图2（b）剪口位于纵筋/横筋距离盒子边缘1/3位置以减小剪口对结构承载的影响。

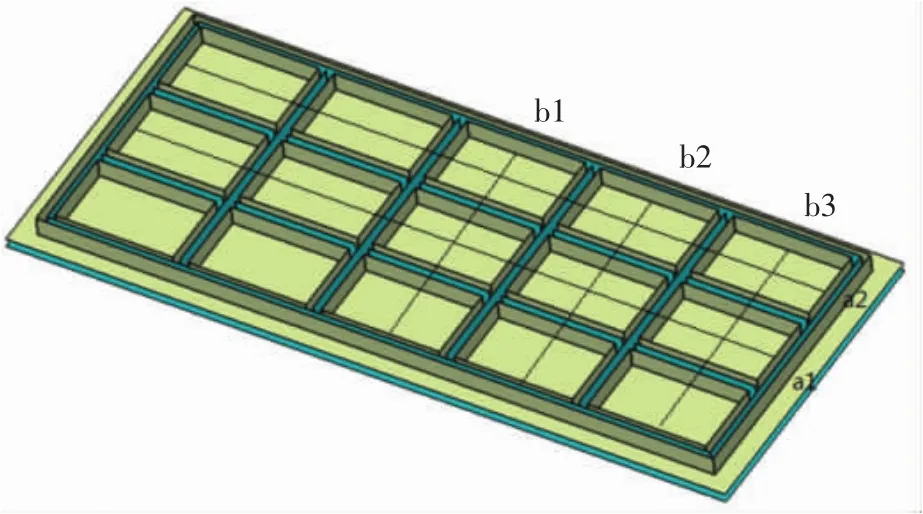
图1 复合材料加筋壁板

图2 复合材料加筋壁板剪口图

对加筋壁板进行充压试验 （见图3），压力达到0.096MPa时试验件有异响，压力剧降，对试验件进行分离，发现试验件在横筋中间（承载最大位置，铺层[4 5/0/45/0/45/45/45/0/45/0/45/0/45]s）和横筋铺层剪口处断裂（铺层[45/0/45/45/45/0/45/0/45/0/45]s）（见图 4）。

图3 复合材料加筋壁板充压试验

2 理论分析

图4 加筋壁板破坏位置

对加筋壁板进行线性/非线性分析，计算应力结果见图5，线性分析结构最大应变为9570，几何非线性分析结构最大应变为9030，均位于边缘螺栓连接位置，为局部应力集中；安全裕度结果见图6，线性计算安全裕度为-0.059，非线性计算安全裕度为0.121，危险点与试验破坏位置一致，说明计算与试验吻合良好；位移结果见图7，线性计算位移为13.1mm，非线性计算为11mm。通过应变、安全裕度、位移结果对比，考虑结构几何非线性，安全裕度由-0.059提高到0.121，结构承载能力提高了19.1%；结构的刚度也有提高，位移从13.1mm减小到11mm，结构刚度提高了18.2%。考虑结构变形后载荷重分配，对结构进行几何非线性分析结构的承载能力（应变、裕度）均有提高。

图5 应变

图6 安全裕度

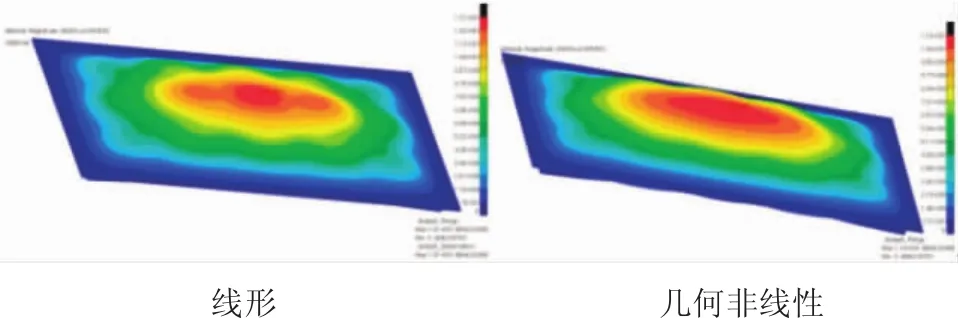
图7 位移

几何非线性分析时对结构变形进行迭代分析，考虑了结构变形以后的刚度变化，线性计算和几何非线性计算结果差异较大。提取图1中纵向（a1、a2）、横向（b1、b2、b3）截面计算结果，见图 8～图 14。

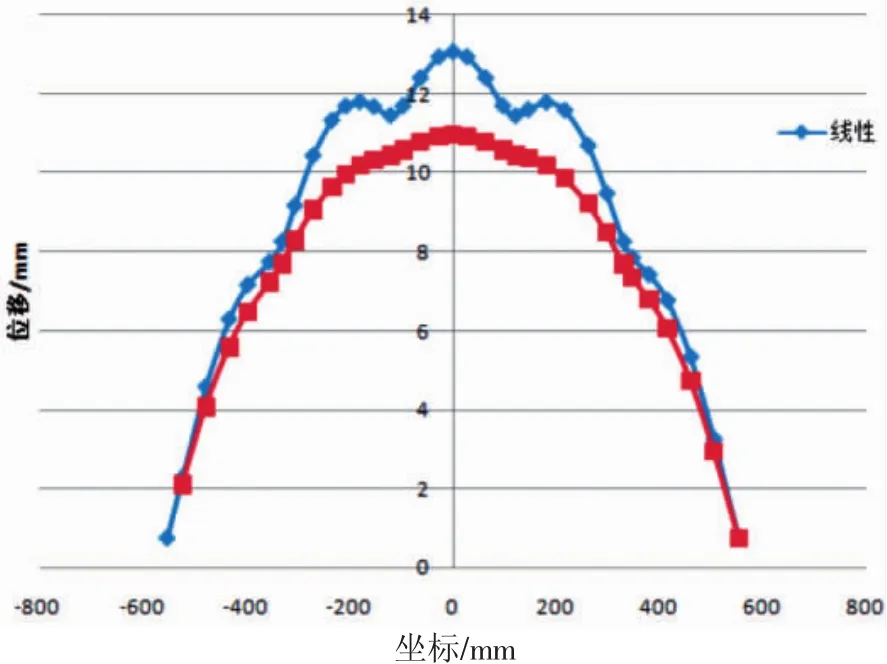
图8 加筋板纵向中线（a1）位移对比

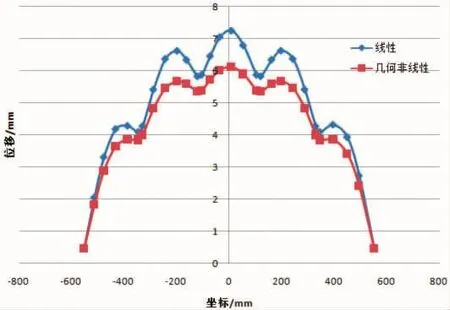
图9 加筋板纵向侧边线（a2）位移

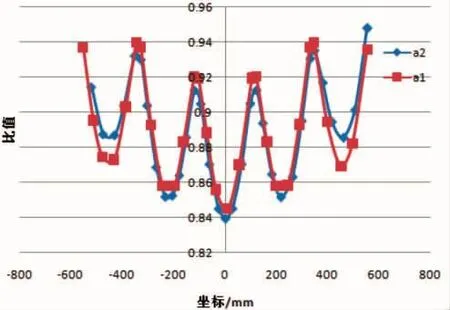
图10 纵边位移比值对比

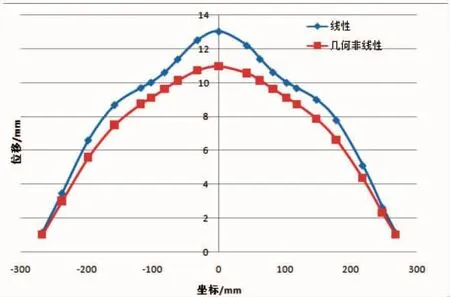
图11 加筋板横向中线（b1）位移

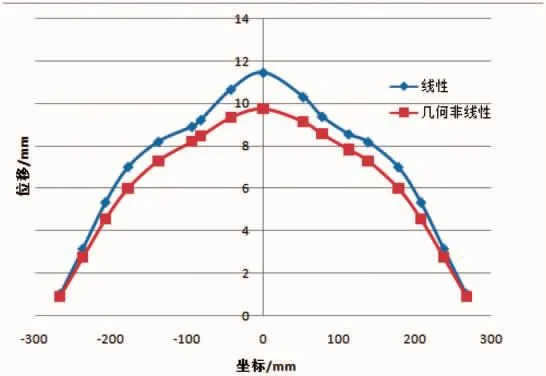
图12 加筋板横向侧边中线（b2）位移

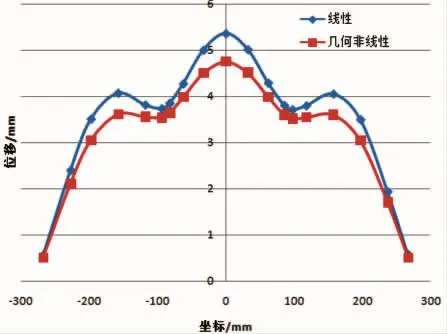
图13 加筋板横向侧边中线（b3）位移

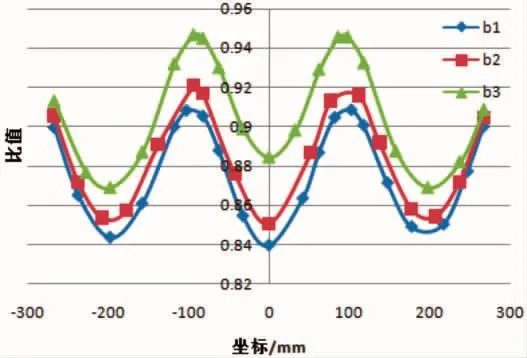
图14 横边位移比值对比

各位置几何非线性计算结果位移均小于线性计算结果，且非线性计算结果纵向和横向位移曲线更为光滑，如图8、图11，几何非线性位移平板中间位置位移曲线比较平顺，纵筋、横筋对结构变形影响较小；在图9、图13中，线性、非线性结果纵横筋对结构的位移影响较大，可以明显看到纵横筋位置结构刚度的变化，结构在有纵横筋的位置位移曲线变缓、刚度有明显提高。这两者的差异主要是由于结构的刚度变化引起，线a1、b1位于加筋板中部，也是纵筋/横筋中间位置，即筋条变形最大、刚度最小的位置，纵横筋对线a1、b2位移约束较小，因而非线性结果比较平滑；而线a2、b3位于纵横筋靠近边缘位置，纵横筋对平板支撑刚度较大，线a2、b3非线性计算位移在纵横筋位置有明显的突变。而对于线性计算结果，所有的分析都是基于平板最初的刚度，未根据结构变形后的刚度进行重新分析，因此在有纵横筋的位置结构位移都有明显变化，线性计算和非线性计算的差异说明了结构变形后载荷重分配对结构变形的影响。

a1、a2、b1、b2、b3 线性、非线性位移结果比值见图 10、图 14，纵边（a1、a2）和横边（b1、b2、b3）两者的比值趋势有明显不同，纵边位移比值a1最大值大于a2，最小值在不同的波峰波谷之间交替出现，两侧的最小值在a1，中间的最小值在a2；而横边则明显b1＜b2＜b3，三条比值曲线为近似平行曲线。位移比值的差异与结构约束和结构形式有关，对于b1、b2、b3三条曲线，其两边支撑条件一样，结构尺寸相同，但是纵筋的支持刚度不同，越靠近边缘，纵筋对结构的支撑刚度越大，即三条曲线刚度排序为b1＜b2＜b3，而对于几何非线性分析结构变形越大，几何非线性对结构变形的影响越大，线性与非线性计算结果的差异也越大，因而存在三条位移曲线比值b1＜b2＜b3，同时三条曲线结构形式一致，其变化规律近似，三条比值曲线近似平行。

a1、a2两条曲线位移比值与上面的分析变化规律有极大不同，这与纵横筋的跨度有关，纵筋的长度大于横筋的，因而横筋刚度要大于纵筋，在横边变形时，纵筋提供的支撑刚度占比较小，因而不能改变整个结构的变形趋势，而对于纵边变形，横筋对结构变形提供的刚度占比更大，因此横筋改变了结构原有的承载分配，相比a2，a1刚度较弱，但是a1、a2纵横筋刚度贡献比也不同，这种刚度的变化会改变结构的几何非线性度，观察图10曲线趋势，加筋板纵向侧边第一方格，两边横筋位置a1非线性度小于a2；方格内部平板区，a1刚度小于a2，其非线性度大于a2，这表明，在第一方格内a1横筋对结构的贡献大于a2；对于中间其他平格，a1非线性度均小于a2，图10中a2非线性位移曲线解释了这种现象，a2非线性位移曲线波折度远大于a1。纵横比位移比值的差异反映结构几何非线性并非单纯的与位移有关，结构形式对几何非线性也有较大影响。

3 结论

本文对复合材料加筋壁板充压进行了试验和理论分析，获得如下结论：

1）线性计算和非线性计算结果均在试验值附近，其计算精度均可接受，但是非线性计算结果位移更符合真实结构，考虑几何非线性，结构刚度提高18.2%，结构承载能力提高19.1%；

2）几何非线性与结构变形有关，同一结构变形越大，几何非线性对结构承载影响越大，结构存在变形较大时应考虑几何非线性以获得较好的计算精度；

3）结构形式对几何非线性分析影响较大，在结构设计中需要进行刚度匹配，以利用结构几何非线性特性获得更好的力学性能。