电池剩余放电时间的预测模型∗
王建芳 丁艾琳
(1.西安铁路职业技术学院 西安 710026)(2.西安交通大学经金学院 西安 710061)
1 引言
铅酸电池广泛应用于电瓶车、电动汽车、清洁车、自行车、老年代步车和自动引导车等。电池的使用量变得越来越大,那么,对于电池的荷电状态和供电时长研究显得尤为重要,提出以下问题:
1)建立同一批次电池以不同电流强度放电的放电曲线模型,并给出其平均相对误差MRE。分别以30A、40A、50A、60A和70A电流强度放电,测得电压都为9.8V时,根据获得的模型求剩余放电时间;
2)建立20A~100A之间任一恒定电流强度的放电曲线模型,并用MRE评估模型的精度。用表格和图形给出55A时的放电曲线;
3)预测电池衰减状态3的剩余放电时间。
(数据来源高教社杯全国大学生数学建模竞赛2016C题)
2 问题分析
问题1)中,首先读取数据,画出散点图,选择预测分析方法,得到放电曲线t=fi(u)模型;其次,从最低保护电压开始以不超过0.005的最大间隔筛选231个电压样本点,计算平均相对误差;最后将电压9.8V代入30A~70A的模型中,求出剩余时间。
问题2)中,在问题1)的基础上,首先找到电流强度与系数之间的关系式,得到t=f(u,i)的通用模型;其次通过计算平均相对误差来评估模型精度;最后利用通用模型求55A时的放电曲线。
问题3)中,首先读取数据,画出散点图,通过回归分析找到4种状态的关系模型,其次,根据模型预测出衰减状态3的缺失数据,最后求出剩余时间。
3 问题1)模型建立与求解
3.1 建立20A~100A各电流强度的放电曲线模型
根据附件1(见2016C)数据,利用Matlab软件[1~5]画出散点图 1,通过分析图像,发现它们有共同的曲线变化趋势,t∝u之间可能存在幂函数或指数函数关系,在此采用多项式拟合[6~8],拟合曲线如图2、3所示(以20A、30A为例)。
20A~100A各放电曲线模型如下:
3.2 MRE计算
MRE的定义:由于放电曲线的预测精度取决于低电压段的质量,所以采样点的选择从最低保护电压Um开始,以最大间隔不超过0.005V选取231个电压样本点,其对应的样本放电时间与模型放电时间的平均相对误差表示如下。

其中,ti为样本放电时间,为模型放电时间,n为样本数,由式(2)计算可得到20A~100A的MRE值如表1所示。

表1 20A~100A的MRE值
由表1可知,平均相对误差的范围在1.5%~3%之间,误差很小,所得放电曲线模型精度满足要求。
3.3 30A~70A剩余放电时间计算
将 u=9V, 9.8V 代入模型(1)电流强度 i=30, 40,50,60,70A的函数关系式中,计算得出其对应的剩余放电时间如表2所示。利用Matlab软件[6~8]画出t∝i变化趋势如图4所示。

表2 30A~70A剩余放电时间表
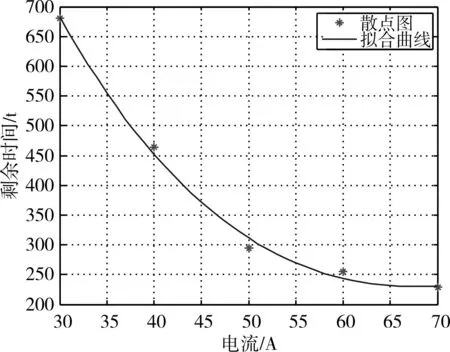
图4 30A~70A剩余放电时间图(9.8V)
由图可知,随着电流强度的增加,剩余放电时间在逐步减少。
4 问题2)模型建立与求解
4.1 任一电流强度的放电曲线模型
根据对问题的分析,需要得到任一电流强度下的放电曲线,需建立电压U、时间t、电流I之间的函数关系式,由问题1可知,电池的放电曲线满足二次函数,并且二次函数的系数随电流的变化而变化,所以建立如下模型:

通过数据拟合[9~11],可得各系数与电流强度的关系如下:
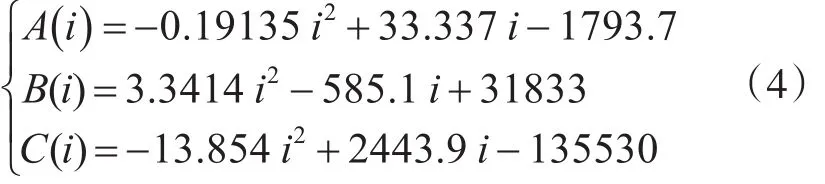
将式(3)和(4)合并可得到 u=f(t,i)的二元函数模型如下:
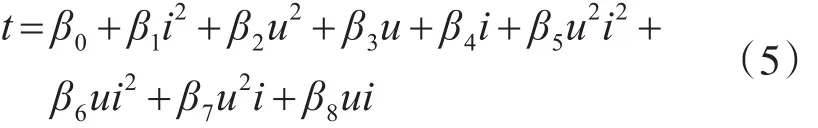
其中系数取值可由A(i),B(i),C(i)的系数确定。
4.2 模型精度评估
通过计算平均相对误差来评估模型的精度。将电流强度 i=20A~100A 代入式(3)和式(4)中,运用Matlab软件和Excel求得各电流强度对应的平均相对误差如表3所示。
对9个平均相对误差进行综合分析,求其平均值为2.8%<3%,在误差范围内,因此模型建立合理,可以推广为一般通用模型。
4.3 电流强度为55A时的放电曲线
将i=55A 代入式(3)和式(4)中,可得到电流强度为55A时的放电曲线模型为


表4 55A时间表
对照2016C附件1数据,55A放电时间均包含在50A~60A之间。

图5 55A剩余放电时间与电压关系图
5 问题3)模型建立与求解
要补充状态3的缺失数据,先对4种状态的样本数据进行关联分析。根据4种状态:新电池状态0、衰减状态1、衰减状态2所给数据,利用Matlab软件作出散点图如图6所示。
由图6可知,4种状态之间逐步衰减,但衰减程度可能不同,在此以相邻状态的数据差值Δti,i+1(i=0,1,2)作为衰减因子,采用多元线性回归法[12~15],以 Δt2,3为因变量,以 Δt0,1,Δt1,2作为自变量,进行多元线性回归分析,则有
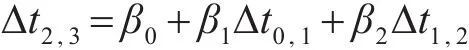

图6 4种状态的的散点图
衰减状态3的预测放电时间为
衰减状态3的预测剩余放电时间为

由以上分析得到模型如下:
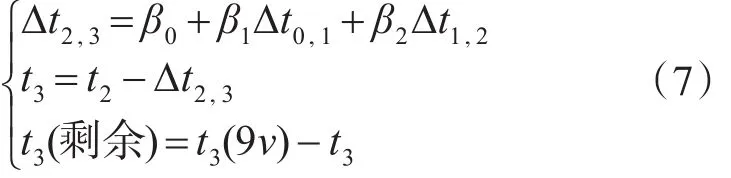
由模型计算可知,R2=99.5% ,p<<α,说明模型是可信的,利用Matlab做出4种状态的放电曲线如图7所示,由此得到衰减状态3剩余放电时间为219.52min。
6 结语
通用模型简单方便,根据不同情况,只要将数据改变代入模型中,即可求任意电流强度的放电曲线。由于数据量大,多次拟合,存在一定误差,但通过MRE评估后,模型可靠,可推广用于生活中的多个领域。

