流体压力对液压管路流固耦合振动特性的影响研究*

安晨亮，马金玉，王阔强

(1.北京航天发射技术研究所，北京 100076；2.北京精密机电控制设备研究所，北京 100076；3.燕山大学 机械工程学院， 河北 秦皇岛 066004)

0 引 言

液压系统以其功重比高的特点被广泛应用于航空航天、船舶、重型机械等工业领域。液压管路作为液压系统的动力传输元件，在传递能量的同时也会受到泵源流量、压力脉动，结构基础激励、外部叠加载荷的作用，从而产生剧烈的流固耦合振动，为液压系统带来振动、噪声问题，威胁系统的可靠性。以航空液压系统为例，据中国民航总局统计，全部飞行事故中有超过30%是由于液压系统管路故障而引起的，而液压管路故障的主要诱因是管路结构变形、发热和振动[1]。随着液压系统不断向高速高压化方向发展，液压管路的流固耦合振动也呈现出频域范围宽、振动幅值大的特点。因此，研究流体参数对液压管路流固耦合动力学行为影响规律，具有重要理论及工程意义。

国外学者很早就开始进行了这方面的研究，在流固耦合模型的建立和求解方面取得了丰富的成果。20世纪初，JOUKOWSKY[2]提出了水锤理论，为后续的流固耦合理论的研究奠定了理论基础；60年代中期，SKALAK[3]对该经典水锤理论进行了扩展，建立了流固耦合4-方程模型，并对水锤理论进行了计算；在此基础上，DAVIDSON[4]完善了4-方程模型，提出了流固耦合8-方程模型，可以充分说明管路的轴向运动和横向运动，并利用传递矩阵法建立了弯曲管路模型，求解了流固耦合8-方程模型，为方程的传递矩阵法求解提供了理论基础。

国内学者也在这方面进行了很多研究，丰富了管路流固耦合振动的研究方向。1999年，焦宗夏[5]考虑简化形式的摩擦项，并利用传递矩阵法对流固耦合14-方程模型进行了求解，得到了摩擦项不会改变管路的固有频率只会影响管路在谐振频率处的响应幅值的结论；同年，张立翔[6]详细论述了4-方程的频域数值解法，利用传递矩阵法对所述模型进行了求解；2002年，刘忠族[7]利用传递矩阵法求解了空间弯曲管路系统的频域响应[8]，与解析解进行对比，证明了其方法的正确性；2011年，柳贡民[9]对流固耦合14-方程模型中不同支撑条件的建立进行了研究，提出了基于弹性支撑条件的14-方程模型；2014年，徐远志[10]在考虑了不同约束条件的影响基础上，分别对不同类型的管路模型进行了建模及求解，方便了复杂管路系统的求解。

本文在考虑泊松耦合作用的基础上，建立液压管路流固耦合14-方程动力学模型，用传递矩阵方法求解不同油液压力下管路轴向速度响应的频域解，并进行液压管路振动测试实验，获取压力对液压管路流固耦合振动特性影响规律。

1 管路流固耦合模型建立及求解

目前，管路流固耦合动力学模型主要有4-方程模型、6-方程模型、8-方程模型和14-方程模型，其中14-方程模型最为完善，被广泛应用于流固耦合振动分析中[11-12]。本文以液压系统直管和弯曲管路为研究对象，进行管路流固耦合理论分析，主要包括14-方程、边界条件和激励条件的建立，同时考虑摩擦耦合对管路流固耦合的影响，建立流固耦合摩擦模型。

1.1 弯曲管路流固耦合14-方程的建立

弯曲管路微元如图1所示。

其中坐标系的定义遵循右手定则，基于De Jong的弯曲管路模型，建立弯曲管路14-方程模型。具体模型如下所列。

(1)轴向动力学模型：

(1)

(2)

(3)

(4)

(2)横向y-z动力学模型：

(5)

(6)

(7)

(8)

(3)横向x-z动力学模型：

(9)

(10)

(11)

(12)

(4)扭转动力学模型：

(13)

(14)

式中：ff—弹性修正因子，ff=1.65r2/eR；ψ—管路弯曲角度，rad。

由于弯曲管路的14-方程模型是由直管路14-方程模型扩展而来，当弯曲半径R→∞时，该模型即为直管路流固耦合动力学模型。

1.2 管路流固耦合摩擦项

流体摩擦项在流固耦合14-方程中的具体形式为流体对管路壁面的剪切力。ZIELKE[13]利用Bessel函数和Laplace变换得出了管路中流体对管壁摩擦的频域摩擦模型，具体表达式为：

(15)

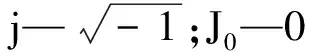
对上述频域摩擦项公式(15)进行拉普拉斯反变换，可以得到时域摩擦公式：

(16)

式中：W—无量纲时间加权函数，τ=νft/R2。

并且，当τ<0.02时：

(17)

当τ>0.02时:

(18)

由流固耦合14-方程模型可知，流体剪切力主要存在于水锤方程(1)中。对水锤方程进行Laplace变换后，将流体剪切力模型代入其中，可得：

(19)

Trikha在时域范围内对摩擦模型进行简化，得到了经典的摩擦模型，其近似式为：

(20)

将Trikha时域简化模型进行Laplace变换，可得到频域下的表达式：

(21)

加权系数mi和ni值如表1所示。

表1 Trikha加权系数mi和ni值

那么就有：

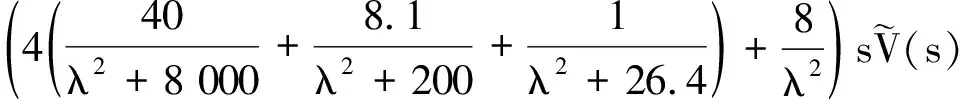
(22)

1.3 管路流固耦合14-方程频域特性求解

根据张立翔对单管的流固耦合14-方程频域求解的阐述，本文依据其求解思想，将流固耦合14-方程统一表示为以下：

(23)

式中：A，B—对时间微分的14阶常数项矩阵和对空间微分的14阶常数项矩阵，分别表示各变量对时间和空间的变化梯度；C—摩擦和粘性阻尼系数；向量r(z,t)—管路的外部激励；Φ(z,t)—管路某轴线截面位置的变量向量。

Φ(z,t)的具体形式为：

(24)

对上述通式进行Laplace变换，可得到：

(25)

式中：所有标注～的向量—含变量s的Laplace变换后的向量。

(26)

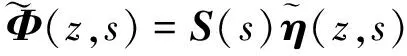
(27)

将式(27)代入方程(26)，可以得到：

(28)

其中：

Λ(s)=S-1(s)A*-1(s)BS(s)

(29)

且：

(30)

为求解方程(28)，Λ(s)须为对角阵。实际上，Λ(s)为A*-1(s)B的特征值，即：

det(B-λ(s)A*(S))=0

(31)

那么Λ(s)可表示如下：

(32)

S(s)为A*-1(s)B的特征向量矩阵，即：

S(s)=(ξ1(s),ξ2(s),Lξ14(s))

(33)

式(28)的一般解为：

(34)

且有：

(35)

(36)

(37)

结合式(27)可得：

(38)

当z=0时，E(0,s)=I，可得：

(39)

将上式代入式(38)，不难看出，管路在任意位置z与位置0处的状态变量间的关系为：

(40)

式中：M(z,s)—管路的“场传递矩阵。

M(z,s)=S(s)E(z,s)S-1(s)

(41)

1.4 单直管路模型求解

对于单根长度为L的管路，其管路边界条件存在于管路两端(z=0和z=L)，各自有7个边界条件，其一般表达式为：

(42)

(43)

式中：D0(s)，DL(s)—管路两端7×14的“边界矩阵”；Q0(s)，QL(s)—管路两端7×1的“激励矩阵”。

建立管路初始端至末端间的状态向量传递关系：

(44)

因此，可以求得管路初始端的状态变量为：

(45)

其中：

(46)

(47)

于是，根据式(45)可求得管路初始位置状态变量，则根据“场传递矩阵”可以得到任意位置的状态变量。

1.5 弯曲管路模型求解

弯曲管路的边界矩阵与激励矩阵的关系可参照单直管路模型求解方式建立。在场传递矩阵建立的过程中，需要对管路中直管单元、弯曲单元和空间弯曲单元，分别建立场传递矩阵，总体场传递矩阵可写为：

Mglobal(L,s)=MN(LN,s)…Mi(Li,s)…M1(L1,s)

(48)

式中：Mi—各管段场传递矩阵；Li—各管段长度。

如果在第i+1段为空间弯曲管路则场传递矩阵可写为：

Mglobal(L,s)=MN(LN,s)…
Mi+1(Li+1,s)Ri(φ)Mi(Li,s)…M1(L1,s)

(49)

式中：φ—第i段与第i+1段相邻坐标系旋转角度，当管路轴向正对观察者时，观察者看到的逆时针即为正向；Ri(φ)—管路坐标变换矩阵。

2 压力对管路振动特性的影响分析

2.1 直管模型

管路支撑方式如图3所示。

图3 直管模型

距管路两端0.25 m处分别设为固定支撑。管路两端自由。将该约束形式下的液压直管可以划分为3段，分别是L1、L2和L3，管路及流体详细参数如表2所示。

表2 直管及流体物理参数

2.2 弯管模型

C919飞机机翼弯曲管路支撑方式如图4所示。

图4 C919飞机机翼弯管模型

同直管安装，故管夹支撑位置认定为是固定支撑。本研究将该约束条件下的管路分成15段在Matlab中进行建模，管路及流体详细参数如表3所示。

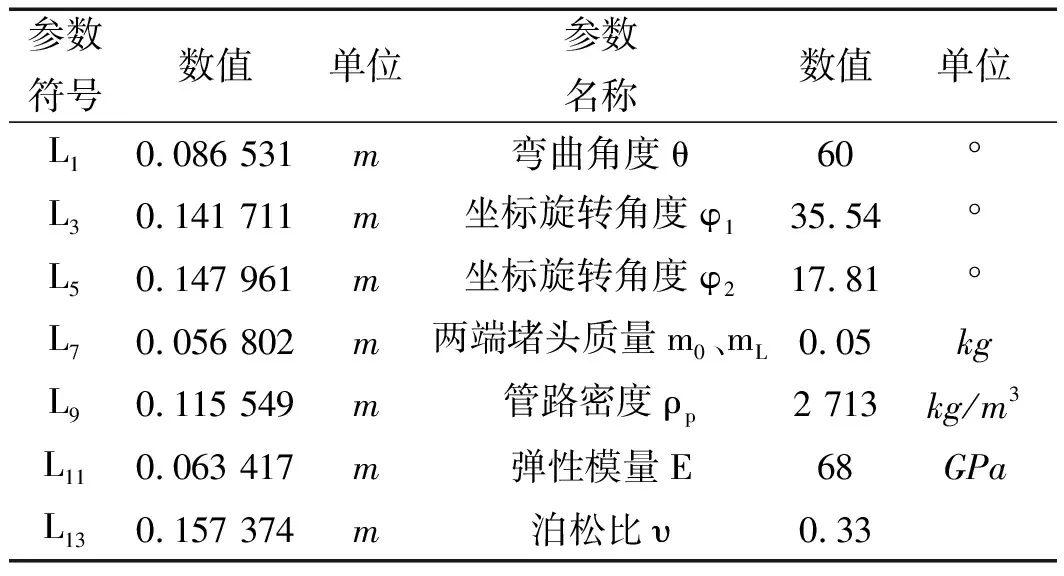
表3 C919飞机机翼弯管结构参数

2.3 压力对管路流固耦合振动特性的影响

随着工艺需求变化，液压系统压力均会不同[11]。调节压力分别为2 MPa、4 MPa、6 MPa和10 MPa(弯管压力只做到6 MPa)。计算导管的振动响应。

节流阀的流量特性通用表达式为:

q=KqAΔPm

(50)

式中：q—流体流量；Kq—节流系数；A—孔口面积；M—与结构有关的参数，0.5≤m≤1。

当m=1时节流阀的流量与压力特性可认为是线性关系，又由于阀出口压力为0，速度为流体与管路管壁之间的轴向相对速度，得：

(51)

那么，当电机转速500 r/min，流量为7.57 L/min，对应压力2 MPa、4 MPa、6 MPa和10 MPa下，得到直管的轴向速度响应如图(5,6)所示。

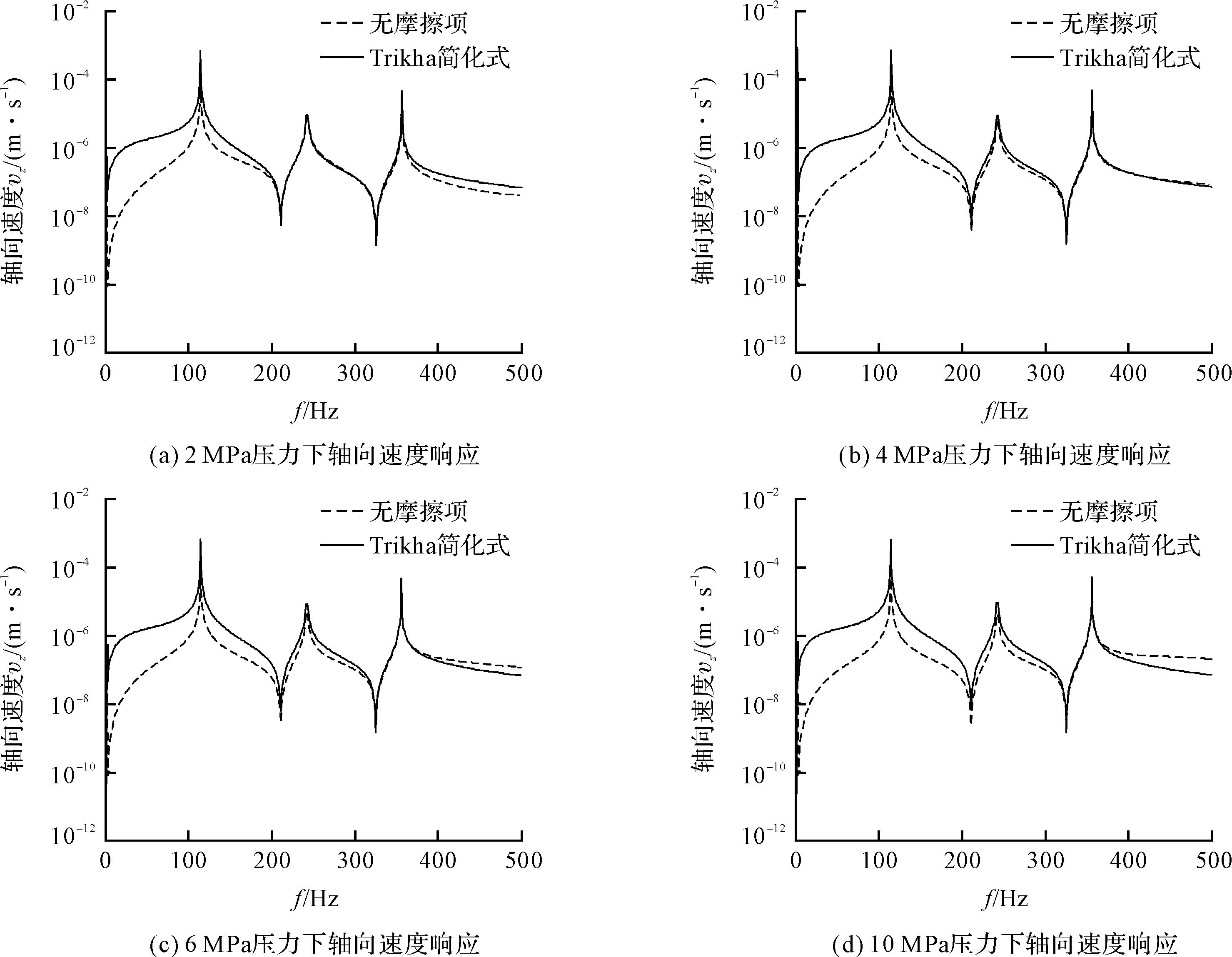
图5 不同压力下直管轴向速度响应曲线

图6 不同压力下弯管轴向速度响应曲线

通过对比不同压力作用下管路轴向速度响应曲线可以看出：随着流体压力增大，管路在高频处响应更为圆滑。这说明流体压力一定程度上会影响管路系统的阻尼，压力越大，阻尼越大。

3 实验研究

3.1 实验台及实验步骤

本文利用搭建的液压管路振动实验台进行实验研究。实验台主要包括液压系统、控制系统和采集系统。液压系统电机转速由电控柜控制，数据采集主要采用NI-PXI来进行，并通过Matlab软件进行数据处理，得出实验结果。

实验设备如图7所示。

管路流固耦合振动实验主要通过NI测试系统设置泵口压力，通过传感器和NI测试系统采集响应压力信号，利用Matlab软件处理实验数据，得出实验频域结果。

3.2 结果分析

当电机转速为500 r/min，流量为7.57 L/min时，调节压力大小分别为2 MPa、4 MPa、6 MPa和10 MPa，(弯管压力只做到6 MPa)。得到管路的轴向振动响应如图(8,9)所示。

图7 实验设备

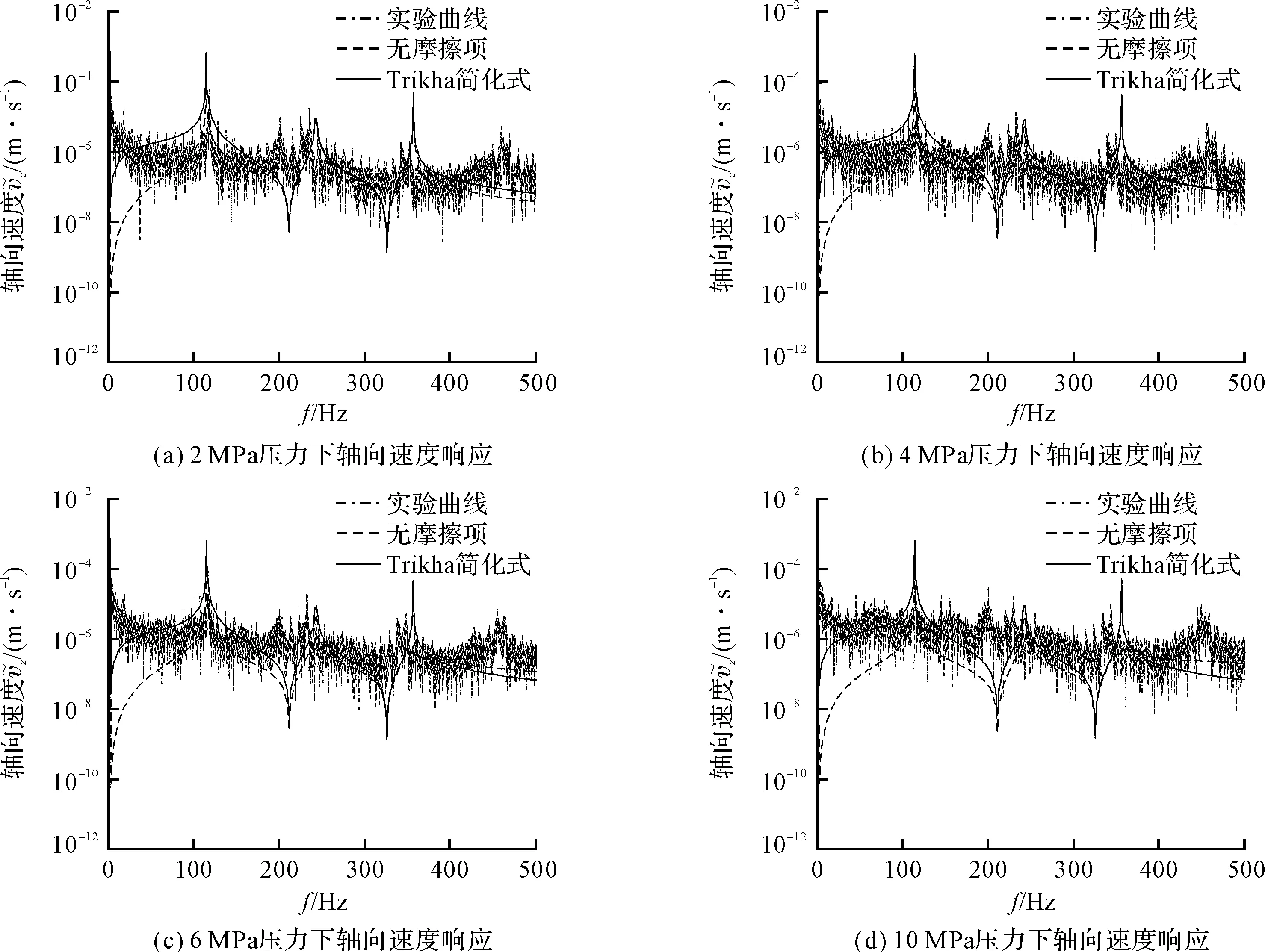
图8 不同压力下直管轴向速度响应曲线

图9 不同压力下弯管轴向速度响应曲线

从图(8，9)轴向速度响应曲线中可以看出：实验得出的谐振频率与数值分析误差不超过10%。但实验曲线中响应幅值较数值分析结果略有减小，这是由于实验中管路支撑和管路两端边界的阻尼较大，一定程度上吸收了管路振动的能量，降低了管路振动的幅值；当流量和脉动频率一定时，随着管路压力的不同，基频基本维持在120 Hz左右，说明压力对管路振动特性影响较小。

4 结束语

本文在理论推导和数值分析的基础上，探究了管路流固耦合振动特性。通过建立考虑摩擦耦合效应的管路流固耦合动力学模型，利用传递矩阵法求解管路轴向振动响应，得到了压力对管路流固耦合振动特性的影响,并通过实验进行了验证,得出了以下结论：

(1)当流体流速和脉动频率一定时，改变管路内介质压力，管路的轴向振动响应变化较小，说明压力对管路轴向振动影响较小;

(2)管路内介质压力的增大，会导致流体与管路之间的阻尼增大，摩擦耦合的影响也会逐渐凸显出来。考虑摩擦耦合作用的管路振动响应结果与实验结果更为相符。