多种空间域滤波方法在大华北地区地壳垂直形变场中的对比分析
畅柳 王宁 时爽爽
摘要: 对中值滤波、模式滤波、盒式滤波、余弦滤波与高斯滤波5种空间域滤波方法的原理及特点进行分析,并对其进行实验模拟,基于模拟试验结果选取高斯滤波应用于大华北地区地壳垂直形变数据优化处理中。结果表明中值滤波适用于背景比较平缓的曲面;模式滤波受突跳空间影响范围最大;盒式滤波对于削弱突跳幅值和突跳空间影响范围效果居中;余弦滤波和高斯滤波的滤波效果接近,但高斯滤波能更好地控制突跳对滤波的影响范围。将空间域滤波方法应用于形变分析数据处理中时,滤波窗口宽度建议选取为削弱目标长半径的2倍。
关键词:中值滤波;模式滤波;盒式滤波;余弦滤波;高斯滤波;形变分析
中图分类号:P315.725 文献标识码:A 文章编号:1000-0666(2018)03-0464-08
0 引言
空间域滤波是一种采用滤波处理的影像增强方法,其理论基础是空间卷积和空间相关。目的是改善影像质量,包括去除高频噪声与干扰、影像边缘增强、线性增强以及去模糊等(郑丽娜等,2012)。采用空间域滤波进行空间信息的残差分离,旨在从观测值中提取出感兴趣的部分(Kim,Wessel,2013)。如在重力位势研究中,需要去除深层结构造成的长波长效应,因为其掩盖了短波长特征(郭志宏等,2003;龚正,许才军,2016;Hillier,Watts,2005);而海洋测深数据的研究方面,在对海洋地壳沉降进行建模时需要区域测深不受小规模特征的影响(Hillier,Watts,2005)。在区域形变分析时,根据实际的需求有时也需要将长波长与短波长的信息进行分离(杨国华等,2001)。大量的实际计算发现利用平滑滤波拟合法能够较好地突出地壳垂直运动信息,消弱地表层的噪声扰动(杨国华等,2001;杨博等,2011)。
在传统的区域水准结果分析中,通常采用剔除异常点、增大绘图时重采样间隔等方法,削弱由于观测点不稳定等因素造成的局部噪声。剔除异常点时,异常点的判断与人的经验相关性较大,常常会出现同一套原始数据不同人处理结果不同的情况,增大绘图时重采样间隔本质上稀释了原始数据也存在一定的缺陷。本文基于对中值滤波、模式滤波、盒式滤波、余弦滤波以及高斯滤波的模拟实验,分析不同滤波的特点,选取较为合适的空间域滤波,将其应用在1990—2010年大华北地区的区域水准得到的垂直形变速率的处理中。
1 几种空间域滤波方法原理
图像处理中经典的滤波模型主要有中值滤波、模式滤波、盒式滤波、余弦滤波以及高斯滤波等,这几种滤波的原理和特征如下所述。
中值滤波与模式滤波属于非卷积滤波。这2种滤波方法的原理差别主要体现在窗口中心点的选取,中值滤波是在滤波窗口的输入信息中提取出中位值作为该窗口中心点的滤波值;而模式滤波主要提取最大似然值作为该窗口中心点的滤波值。盒式滤波、余弦滤波和高斯滤波都属于卷积滤波,滤波后的值与滤波窗口内的每一个值都存在直接关系,而其权重取值不同决定了这几种滤波的差异。
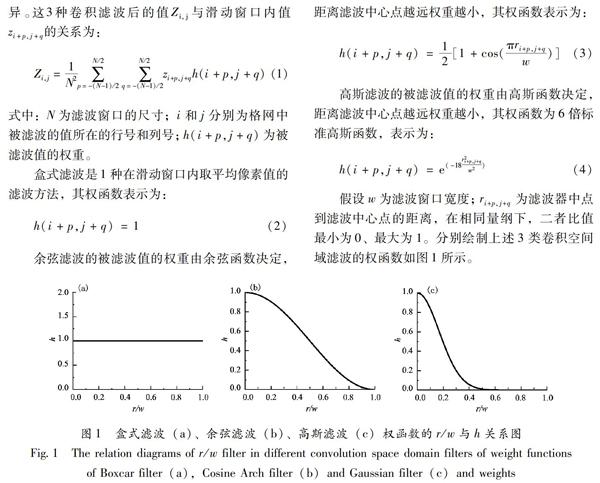
盒式滤波的权重为单位权重,与被滤波点与滤波中心点的距离无关,相当于滤波窗口内的值取平均。对于余弦滤波,当被滤波点到滤波中心点的距离为0时,权重为1,随着滤波器中点到滤波中心点的距离增加,权重降低,直至滤波器中点到滤波中心点的距离等于滤波窗口宽度时权重为0。对于高斯濾波器,当被滤波点到滤波中心点的距离为0时,权重为1,随着滤波器中点到滤波中心点的距离增加,权重快速降低,直至滤波器中点到滤波中心点的距等于滤波窗口宽度时权重为0。高斯滤波比余弦滤波权重降低更快,在滤波器中点到滤波中心点的距离等于滤波窗口宽度的0.5倍左右时权重已经接近于0。
2 模拟实验
为了比较不同空间域滤波方法的滤波效果,模拟一个无量纲的带有突跳的平面,突跳的半径为3,参考Kim和Wessel(2013)的做法,将滤波宽度设置为目标半径的2倍,也就是6。模拟的原始面如图2a所示,假设我们的目标是要将这一突跳在大背景中消除,如图2b所示,不同滤波方法的结果如图2c~i所示。
中值滤波和模式滤波都可将突跳剔除,为了比较这2种滤波方法的滤波效果,分别采用长度为6和3的滤波窗口宽度进行模拟试验(图2c~f)。对于平面上的突跳,滤波窗口宽度选取合适,中值滤波与模式滤波都可以较好地剔除突跳(图2c,e);如果滤波窗口宽度选取较小(图2d,f),中值滤波对突跳的削弱效果优于模式滤波。
3种卷积滤波中,盒式滤波由于是求取滤波窗口的平均值,滤波后突跳的峰值降低明显(图3e),但是其影响范围也明显扩大;余弦函数滤波与高斯滤波相比,滤波效果差异不大(图3h,i),但高斯滤波权重随距离收敛的更快。滤波函数模型和模型测试结果显示平面上的突跳对高斯滤波的影响范围比余弦函数滤波小。
在实际的速率面中,平面带突跳的情况是较少的,大多数情况下都是在缓和的曲面上有一些突跳。因此,我们模拟一个带有突跳的斜面,
突跳半径为3,同样将滤波宽度设置为目标半径的2倍,也就是6,不同滤波方法的滤波结果如图3所示。
从图3c~g中可以看出,高斯滤波和余弦函数滤波结果相近,从滤波原理也可以看出它们的加权方法都是离滤波中心越近权重值越大,只是权函数有所不同。如果在要保留滤波对象的特征的前提下进行滤波,这2种方法更合适,且二者差异不明显,从权值函数的函数特性上,高斯函数收敛更快,更能突出滤波对象的特征。
中值滤波器和模式滤波器在平面中有突跳的情况下滤波效果非常好,可以消除突跳,但是模式滤波在斜面有突跳的情况下对背景信息(斜面)影响比较大。因此除非有特殊需求,不建议使用模式滤波。盒式滤波器在平面有突跳的情况下在削弱突跳方面较高斯滤波和余弦滤波器效果好,但是对背景信息有一定范围的影响。
通过上述的试验认为,对于要剔除或削弱突跳信息,且要尽量少地对背景信息造成影响的需求下,在比较平缓的背景曲面上建议采用中值滤波,在背景曲面起伏波动较大的情况建议采用卷积滤波,且优先考虑高斯滤波。在实际的应用中,应该根据具体的需求选择合适的滤波器和滤波窗口宽度,也可以多种滤波器配合使用。
3 空间域滤波在垂直形变中的应用
为了讨论采用模拟数据分析优选的滤波方法在实际形变数据处理中的应用效果,收集大华北地区1990年前后和2010年前后2期的水准资料,采用分段动态线性速率模型计算垂直运动速率(田晓等,2018)(图4,5中简记为1990—2010年),选取玉渊潭原点为起算点,得到相对速率场(杨国华等,2001;郭宝震等,2017;孙启凯等,2017;苏建锋,薄万举,2016)。2期的原始速率矢量如图4a所示,数据的公共测点为300个,公共测点平均间距约为8.7 km,选取略小于其间距0.05°(约5.5 km)的数据插值间隔进行格网重采样,绘制等值线,如图4b所示。图4b中等值线结果中仍然有一些小的或正或负的突跳(等值线中的小圆圈)。等值线图像上反映的目标突跳长半径最大约为0.25°,因此滤波窗口设定为0.5°,并选用高斯滤波器进行滤波,结果如图4c所示。
从图4c中可以看出,滤波窗口为0.5°的高斯滤波很好地保留了原始的背景运动信息,剔除了大部分的突跳信息。为了对比不同滤波窗口宽度的滤波效果,再选取滤波窗口宽度分别为1.5°,2.0°,3.0°的滤波窗口进行高斯滤波,结果如图5所示。
从图5中可以看出,小于0.5倍滤波窗口宽度的信息几乎都被削弱或消除,滤波窗口宽度越大,剔除掉的信息越多。滤波窗口宽度为1.5°和2.0°的高斯滤波后,宝坻沉降区和呼和浩特沉降区已无法辨识,包头、大同、太原、北京沉降区还能辨识但是幅度明显降低。以2.0°滤波窗口宽度滤波后的沉降幅度更小。经过 3.0°滤波窗口宽度的高斯滤波后,小尺度的形变信息几乎都被剔除,可以明显看到该区域东南降西北升的大尺度形变信息。
水准资料在地震预测的应用中,区域隆升可能具有更强的预测意义,且区域隆升受观测环境影响的可能性较小。因此,在滤波过程中,应当考虑滤波的方向性,以完整保留区域隆升的信号。对上述滤波方法及滤波窗口宽度进行比较,选取滤波窗口宽度为0.5°的高斯滤波,进行优化:原始数据中的正值区域不进行滤波,仅对负值区域进行滤波,结果如图6所示。对比图6与图4b可以看出,优化后的方法完整保留了原始数据的正值区域的形变信息,负值区域的沉降区的大部分突跳信息也得以剔除或削弱。
4 结论
本文对2种非卷积滤波、3种卷积滤波方法进行了对比分析及模拟实验,并将其应用于于大华北地区地壳垂直形变数据优化处理中。研究结果表明中值滤波在带突跳的平面中能较好的消除突跳,但在带突跳的斜面受突跳的影响范围较大,因此适用于背景运动较为平缓的区域;模式滤波受突跳影响范围最大,除非有特殊需求一般不建议使用;盒式滤波在削弱突跳幅值方面弱于2种非卷积滤波,在卷积滤波中效果最好,但其受突跳影响空间范围较大;余弦滤波和高斯滤波在削弱突跳幅值方面较弱,但是可以较好地兼顾削弱突跳的影响和保持背景信息,高斯滤波权函数的特性决定了其能更好的控制突跳对滤波的影响范围。
通过不同尺度的空间域滤波可以得到不同尺度的形變信息。小尺度滤波可以滤掉一些空间小突跳,大尺度滤波可以得到研究区域的背景运动趋势,在此基础上进行格网点加减运算还可以得到扣除背景运动趋势之后的细部相对运动状态。该方法的应用需要对不同空间、不同尺度的研究对象进行探索,本文目前仅提出了该方法应用的可能性,后续还需要进行更细致的研究。
参考文献:
龚正,许才军.2016.日本东北大地震引起的洋底地壳和海水质量重分布效应分析[J].大地测量与地球动力学,36(5):377-379,385.
郭宝震,闫琳琳,叶庆东.2017.基于水准与重力资料的首都圈地区形变分析[J].测绘科学,42(12):88-91,97.
郭志宏,刘浩军,熊盛青.2003.平面网格位场数据的空间域非线性曲率滤波方法[J].地球物理学进展,18(1):134-137.
苏建锋,薄万举.2016.高噪声背景下GNSS垂向分量应用探讨[J].地震,36(1):105-116.
孙启凯,池国民,徐东卓.2017.首都圈地区地壳垂直形变特征及剖面分析[J].大地测量与地球动力学,37(5):497-501.
田晓,郑洪艳,苏广利,等.2018.多面函数和移动法综合模型支持下的区域垂直形变场拟合[J].测绘通报,(2):41-45,88.
杨博,张风霜,韩月萍,等.2011.球面水平应变场无偏计算的实现与滤波[J].地震研究,34(1):59-66.
杨国华,王敏,韩月萍.2001.华北中北部地壳运动与张北地震[J].中国地震,17(3):304-311.
郑丽娜,张涛,匡海鹏,等.2012.基于线阵CCD空间滤波效应的航空相机像移速度测量方法[J].光学学报,32(11):109-115.
Hillier J K,Watts A B.2005.Relationship between depth and agein the North Pacific Ocean[J].Journal of Geophysical Research Atmospheres,110(B2):B02405,doi:10.1029/2004JB003406,2005.
Kim S,Wessel P.2013.Directional median filtering for regional-residual separation of bathymetry[J].Geochemistry Geophysics Geosystems,9(3):Q03005,doi:10.1029/2007GC001850.
Abstract In this paper,principle and characteristics of five filter type which is the Median Filter,Mode estimator Filter,Boxcar Filter,Cosine Arch Filter and Gaussian Filter are studied,and selected a suitable method in north China vertical deformation analysis.The results show that the Median Filter is suitable for the background which is smooth surface.The effect of Mode estimator Filte,in the spacial scale impact by the cone is maximum.The effect of Boxcar Filter,in reducing the amplitude of the cone amplitude and the spacial scale impact by the cone is median.The effect of Boxcar Filter and Gaussian Filter are close,and Gaussian filter can better control the influence area range of the cone the filter.When the filter is applied to the deformation analysis,the filter window width is recommended to twice of the target radius.
Keywords:Median Filter;Mode estimator Filter;Boxcar Filter;Cosine Arch Filter;Gaussian Filter;Deformation Analysis

