Exact Boundary Controllability on a Planar Tree-LikeNetwork of Vibrating Strings with DynamicalBoundary Conditions

Tatsien Liand Yue Wang

1School of Mathematical Sciences,Fudan University&Shanghai Key Laboratory for Contemporary Applied Mathematic&Nonlinear Mathematical Modeling and Methods Laboratory,Shanghai 200433,P.R.China;

2School of Mathematical Sciences,Fudan University,Shanghai 200433,P.R.China.

Received March 13,2018;Accepted April 27,2018

Abstract.This paper concerns a planar tree-like network of vibrating strings with point masses at the nodes.We use a constructive method with modular structure to get the ’one-sided’exact boundary controllability for this system with dynamical boundary conditions.Moreover,by constructing the ’longest’chain-like subnetwork and its’midpoint’,we divide the whole tree-like network into two tree-like sub-networks,and prove the ’two-sided’exact boundary controllability.

Key words:A planar tree-like network of vibrating strings,dynamical boundary condition,exact boundary controllability.

1 Introduction

On a planar tree-like network of vibrating strings,the exact boundary controllability for linear wave equations with Dirichlet boundary conditions was studied in[1]-[2]and[8].In the quasilinear case,by establishing the semi-global piecewiseC2solution for quasilinear wave equations with Dirichlet,Neumann,Robin and dissipative boundary conditions on a planar tree-like network of strings,Gu&Li([3])got the ’one-sided’exact boundary controllability,respectively.Thus,if the network hasksimple nodes,then the ’one-sided’exact boundary controllability can be obtained by means of boundary controls acting on(k−1)simple nodes.

For 1-D elastic strings with tip-masses at the ends,based on the theory of semi-globalC2solution to the corresponding mixed problem,we have established the local exact boundary controllability for(a coupled system of)quasilinear wave equations with dynamical boundary conditions in[9,10]by means of a constructive method with modular schedule(see,e.g.,[5,6]).

In this paper,we consider a planar tree-like network of vibrating strings with point masses at the nodes.Dynamical boundary conditions are encountered in analyzing mechanical behavior of point masses at the simple nodes.While,on the multiple nodes,through the continuity of displacements and the corresponding total stress boundary condition,the interface conditions are obtained.For a tree-like network withksimple nodes,we get its’one-sided’exact boundary controllability by only(k−1)controls given on simple nodes,which is consistent with the result without point masses in[3].Moreover,this paper examines the’two-sided’exact boundary controllability for the first time,that is,the controls are given on all the simple nodes.This result not only leads to a significant reduction of controllability time,but also applies to the case without point masses at nodes,which can be regarded as an important complement to the results in[3].

This paper is organized as follows.The mathematical model and main results of’onesided’and ’two-sided’exact boundary controllability on a planar tree-like network are presented in Section 2.To prove these results,in Section 3,we first establish the existence and uniqueness of semi-global piecewiseC2solution to the corresponding mixed problem on a planar tree-like network.Then based on this,we prove the ’one-sided’exact boundary controllability for this system in Section 4 by constructing the semi-global piecewiseC2solution,which satisfies simultaneously the initial condition,the final condition,all the given boundary conditions and all the interface conditions.Then,in Section 5,we construct the ’longest’chain-like subnetwork and its’midpoint’,and divide the whole tree-like network into two tree-like sub-networks artificially,then finish the proof of the ’two-sided’boundary controllability.

2 Modeling and main results

In this section,we consider a planar tree-like network which is composed ofN(N>1)vibrating strings:S1,...,SN.Without loss of generality,we suppose that one end of stringS1is a simple node.We take this simple node as the starting nodeEof the network.For stringSi,let nodedi0(noded10is justE)and nodedi1be its two ends,thex−coordinates of which arex=di0andx=di1,respectively.AndLi=di1−di0is the length of stringSi.We always suppose that nodedi0is closer toEthan nodedi1in the network,and all nodes are with unit mass(See Figure 1).The case without masses at nodes can be treated in a similar and simpler way.

LetMandSbe two subsets of{1,...N},M∪S={1,...N}.i∈Mif and only ifdi1is a multiple node,while,i∈Sif and only ifdi1is a simple node.Thus,the collection of simple nodes on the network consists ofEand{di1,i∈S},while,the set of multiple nodes is{di1,i∈M}.

Fori=1,...,N,we consider the following quasilinear wave equations on the stringSi(see[3]):

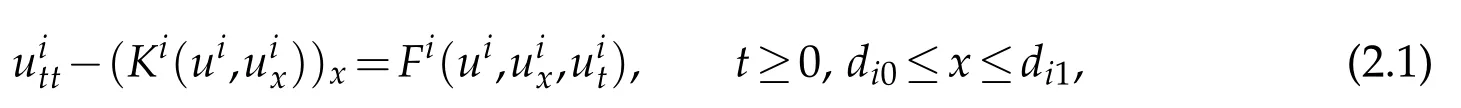
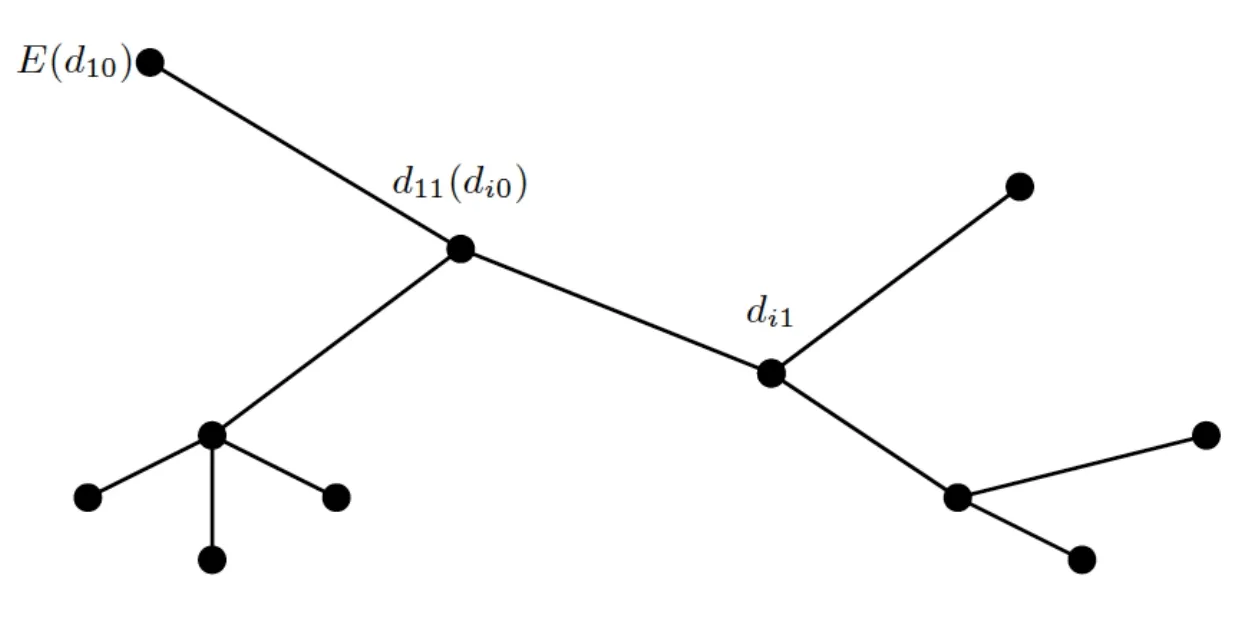
Figure 1:Planar tree-like network with point masses at nodes.

whereKi=Ki(u,v)is a givenC2function ofuandv,such that

andFi=Fi(u,v,w)is a givenC1function ofu,v,w,satisfying

Without loss of generality,we assume that

The initial condition is given by

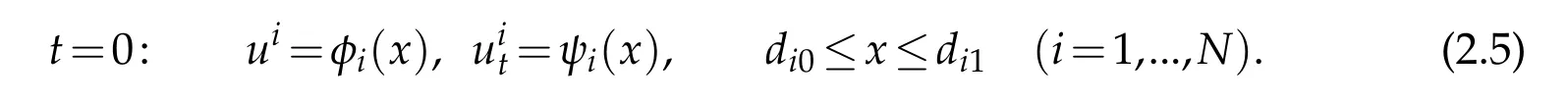
At any given simple nodeEordi1(i∈S),the nonlinear dynamical boundary condition is given as

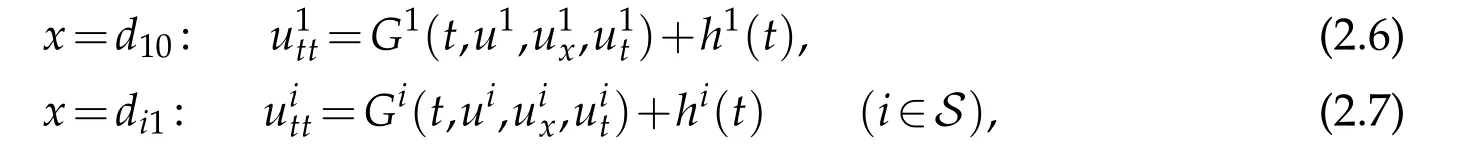
whereGi=Gi(t,ui,,)is aC1function of its arguments andhi(t)is aC0function oft(i=1 ori∈S),and the conditions ofC2compatibility are satis fied at the points(t,x)=(0,d10)and(0,di1)(i∈S),respectively.Moreover,without loss of generality,we may assume that

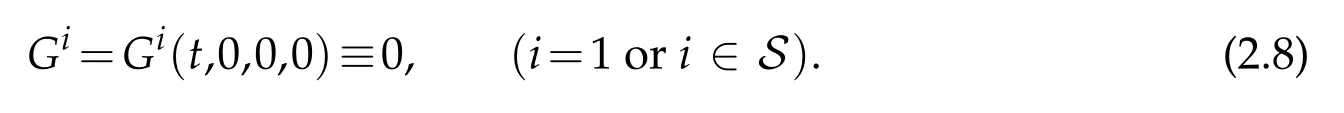
While,on the multiple nodedi1(i∈M),we have the interface conditions:

whereHi(t)is aC1function oft,andJidenotes the set of all the indicesjsuch thatdj0is just the nodedi1(see Figure 2).

Since there is no loop in the tree-like network,for any given indexi∈S,there exists a unique chain-like subnetwork connecting nodesEanddi1(i∈S).Distands for the set of indices corresponding to all the canals in the unique chain-like subnetwork connecting nodesEanddi1(i∈S),and for simplicity,Dialso stands for this chain-like subnetwork(see Figure 2).

Figure 2:For multiple node d11,J1={2,3};for simple node d91D9={1,3,8,9}.

Theorem 2.1.[One-sided exact boundary controllability]Let

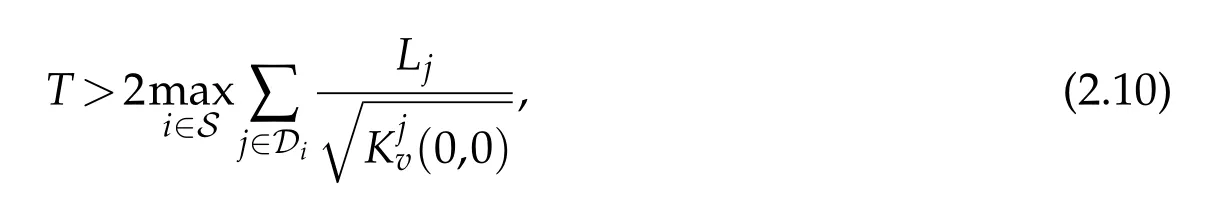
for any given initial data(φi,ψi)(i=1,...,N)and final data(Φi,Ψi)(i=1,...,N)with small norms

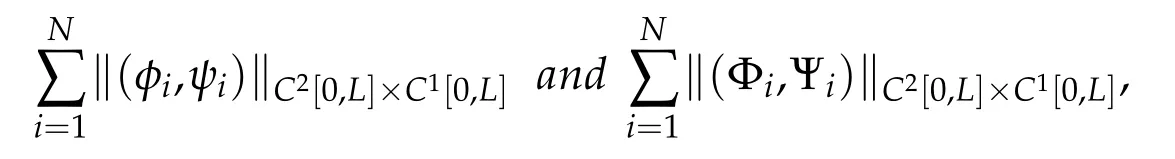
and for any given function h1(t)(h1(t)≡0or h1(t)∈C1[0,T]with small C1norm)in the boundary condition(2.6)on the starting node E and any given functions Hi(t)∈C1[0,T]with small C1normsintheinterfacecondition(2.9)onallthemultiplenodes di1(i∈M),suchthattheconditionsof C2compatibility or piecewise C2compatibility are satisfied at the points(t,x)=(0,d10),(T,d10)and(0,di1),(T,di1)(i∈M),respectively.Suppose furthermore that

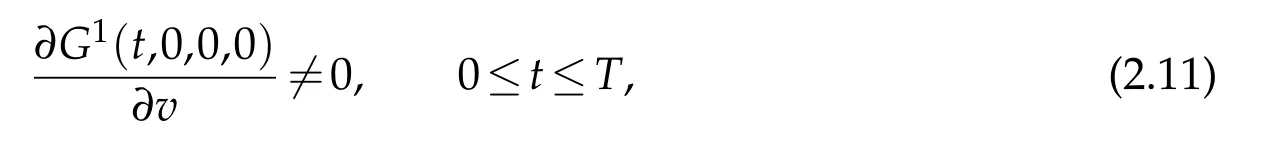
where v denotes the third argument of function G1.Then,there exist boundary controls hi(t)withsmall normson all the simple nodes except the starting one,such that on thedomainR(T)=(t,x),0≤t≤T,di0≤x≤di1},the mixed initial-boundary value problem for system(2.1)with(2.5)-(2.9)admits a unique piecewise C2solution ui=ui(t,x)(i=1,...,N)with small piecewise C2norm,which exactly satisfies the final condition:

The above result can be considered as a generalization of the’one-sided’exact boundary controllability considered in[3]in the case with masses at the nodes.Furthermore,we can also examine the corresponding ’two-sided’exact boundary controllability.For the convenience of description and proving,we first define a ’longest’chain-like subnetwork,and choose the simple nodeEas the starting node for this ’longest’one.For this purpose,we assume that the tree-like network hasmsimple nodes:E1,E2,...,Em.Let={1,...,m}.For any giveni,j∈,i6=j,there is a unique chain-like subnetwork connecting simple nodesEiandEj.LetDijdenote not only the set of indiceskof all stringsSkcontained in this subnetwork,but also the subnetwork itself.

Definition 2.1.The ’length’of the chain-like subnetwork connecting simple nodesEiandEjis defined as

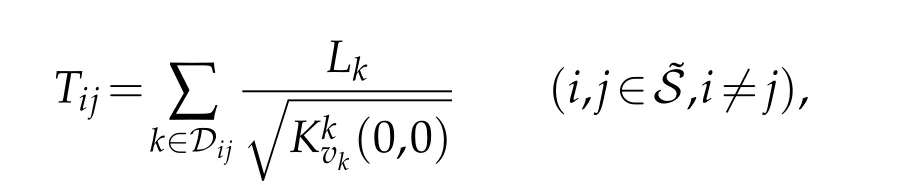
wherevkisthe second argument of functionKk.Noting thatN>1 andNis finite,we can findi0,j0∈(i06=j0),such that

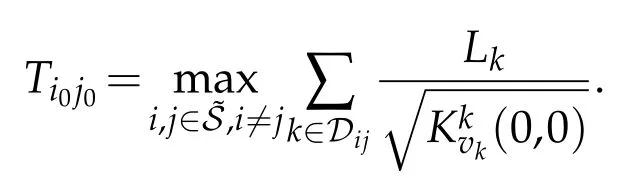
Thechain-likesubnetworkbetweenEi0andEj0isdefinedasa ’longest’chain-likenetwork in this tree-like network.Then,a simple node of the ’longest’chain-like network is taken as the starting node of the whole network,and we can rewrite the ’length’of the ’longest’chain-like network as

Theorem 2.2.[Two-sided Exact Boundary Controllability]Let

whereis given by(2.13).For any given initial data(φi,ψi)(i=1,...,N)and final data(Φi,Ψi)(i=1,...,N)with small norms

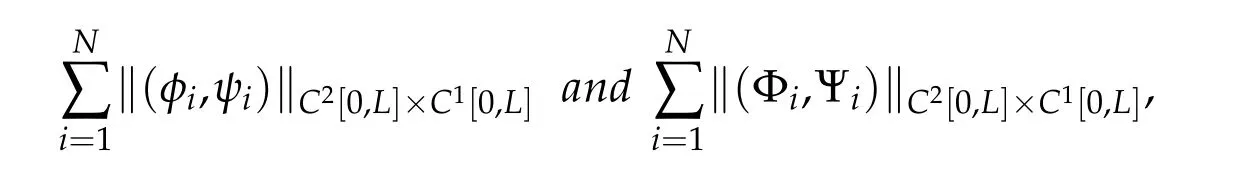
and for any given functions Hi(t)∈C1[0,T]with small C1norms in the interface condition(2.9)on all the multiple nodes di1(i∈M),such that the conditions of piecewise C2compatibility are satisfied at the points(0,di1)and(T,di1)(i∈M),there exist boundary controls hi(t)withsmall normson all the simple nodes,such that on the domainR(T)={(t,x),0≤t≤T,di0≤x≤di1},themixedinitial-boundaryvalueproblemforsystem(2.1)with(2.5)-(2.9)admits a unique piecewise C2solution ui=ui(t,x)(i=1,...,N)with small piecewise C2norm,which exactly satisfies the final condition:

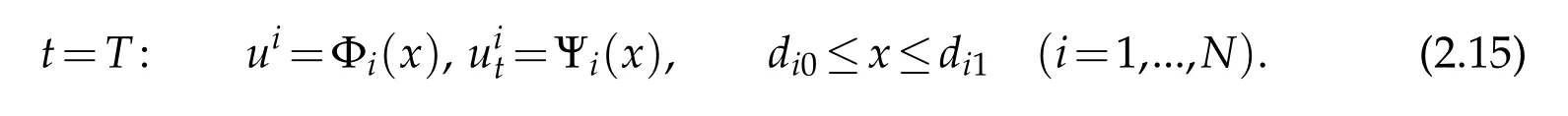
3 Existence and uniqueness of semi-global piecewise C2solution

In order to obtain the exact boundary controllability for system(2.1)with dynamical boundaryconditionsandinterfaceconditions(2.7)-(2.9)onatree-likenetwork,weshould first prove the existence and uniqueness of semi-global piecewiseC2solution to the corresponding mixed initial-boundary value problem.To this end,we reduce wave equations(2.1)to a first-order quasilinear hyperbolic system.

Let

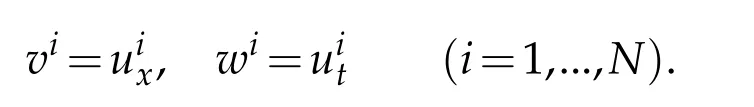
Fori=1,...,N,system(2.1)can be reduced to

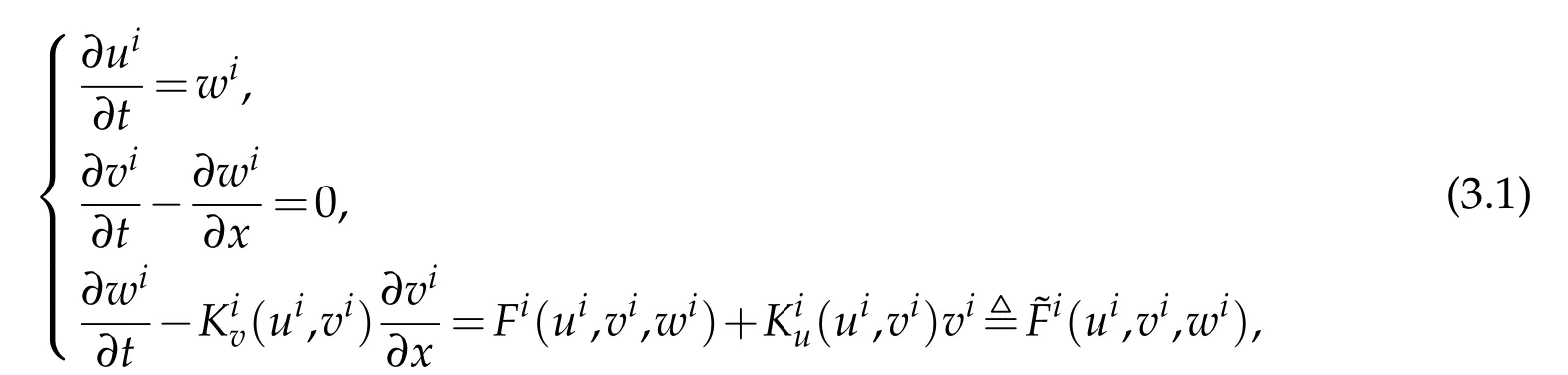
Noting(2.2),(3.1)is a distinct hyperbolic system with 3Nreal eigenvalues:

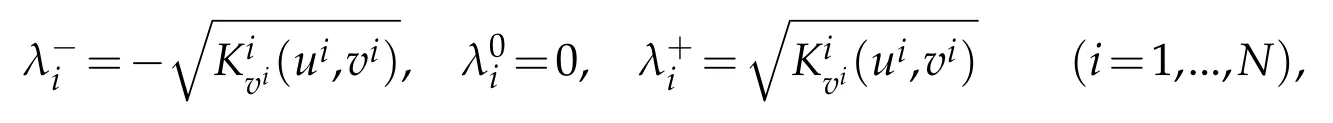
and the corresponding left eigenvectors can be taken as

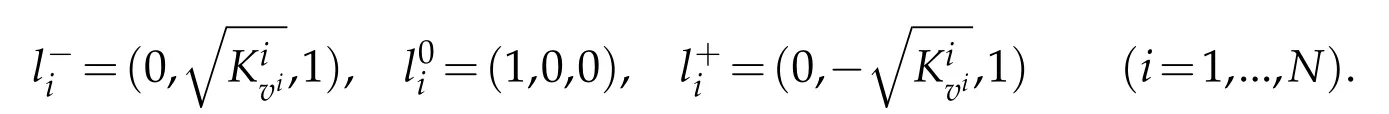
Let

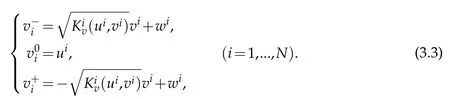
Noting(2.2),in a neighborhood of(ui,vi,wi)=(0,0,0),by the Implicit Function Theorem,(3.3)can be rewritten as

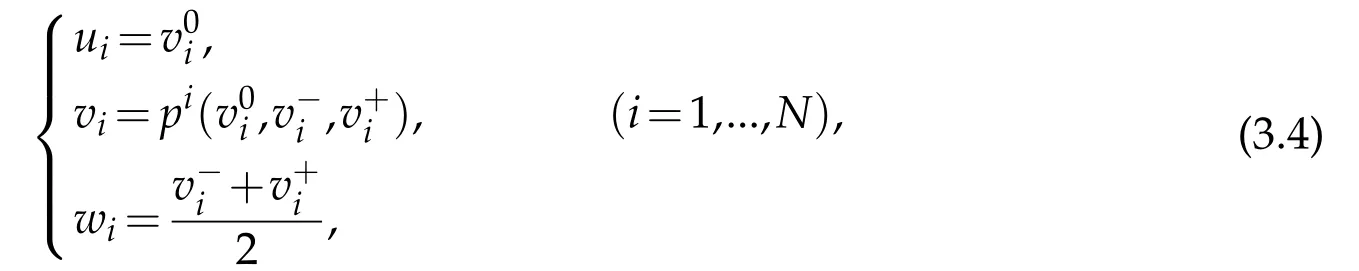
wherepiis aC1function of its arguments.

The initial condition(2.5)now becomes

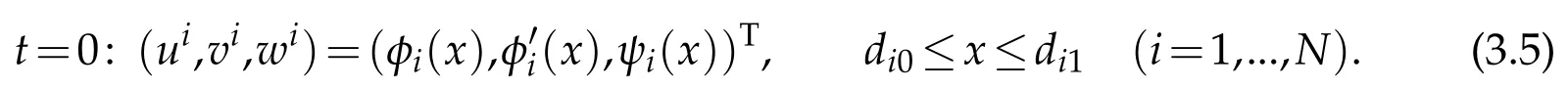
On simple nodeEanddi1(i∈S),the dynamical boundary conditions(2.6)and(2.7)can be correspondingly replaced by the following nonlocal boundary conditions[9],

Noting(3.3)-(3.4),the nonlocal boundary conditions above can be rewritten as,

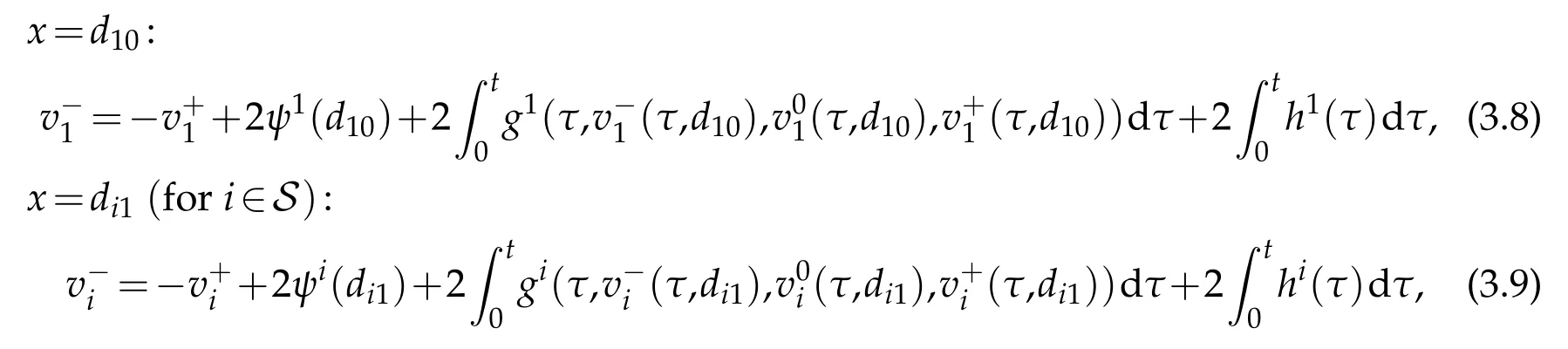
where

While,noting the conditions of compatibility atmultip lenodedi1(i∈M),the interface condition(2.9)can be replaced by

then it can be rew ritten as

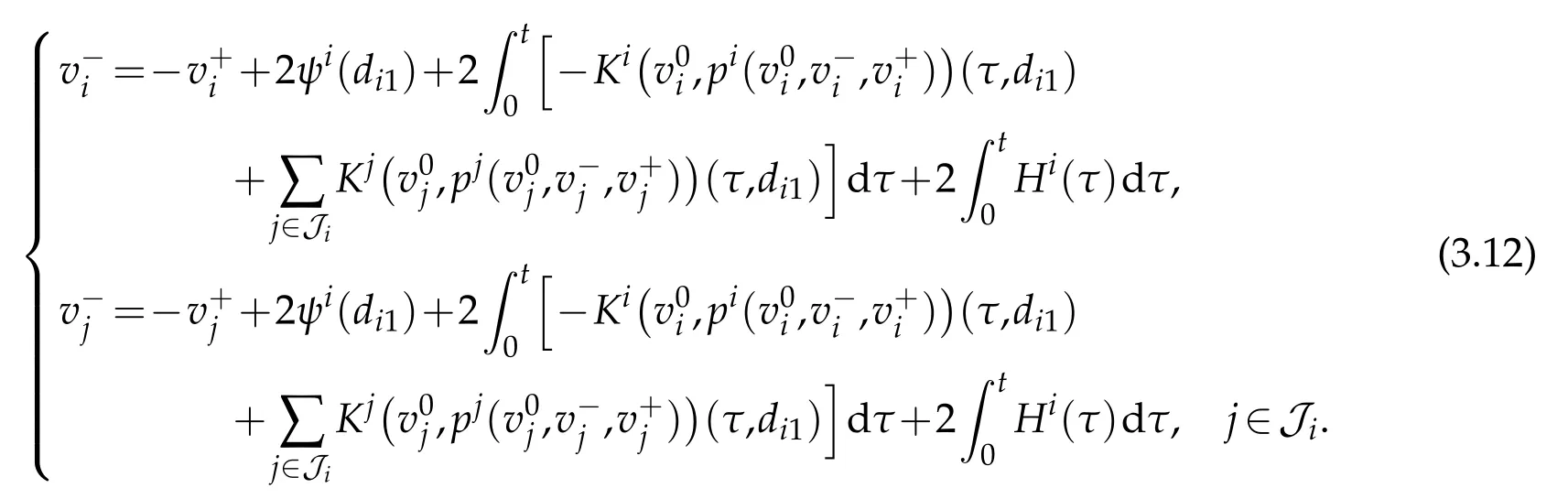
Applying the resulton the semi-global C1 solution to a first-order quasilinear hyperbolic system with zero eigenvalues associated with a kind of non local boundary condition(see[9]),we can obtain the following

Lemma 3.1.Under the assumptions given at the beginning of Section 2,for any given T>0,sup-pose thatM)are small enough(depending on T),and the conditions of C2compatibility or piecewise C2compatibility are satisfied at the points(t,x)=(0,d10),(0,di1)(i∈S)and(0,di1)(i∈M),respectively.Then,the forward mixed initial-boundary value problems(2.1)and(2.5)-(2.9)admit a unique piecewise C2solution ui=ui(t,x)(i=1,...,N)with small piecewise C2norm on thedomain

Similar resu lt can be obtained for the backw ard mixed p roblem(2.1)(2.7)-(2.9)and(2.12)with the final condition

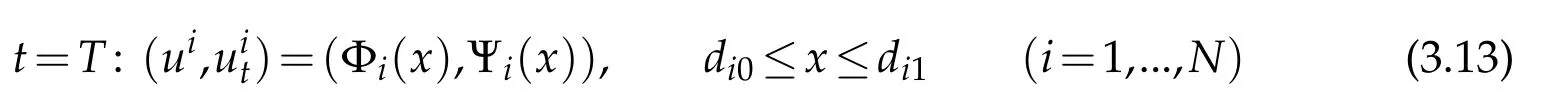
as follow s.

Lemma 3.2.Under the assumptions given at the beginning of Section 2,for any given T>0,sup-pose thatM)are small enough(depending on T),and the conditions of C2compatibility or piecewise C2compatibility are satisfied at the points(t,x)=(T,d10),(T,di1)(i∈S)and(T,di1)(i∈M),respectively.Then,the backward mixed initial-boundary value problems(2.1),(2.7)-(2.9)and(3.13)admit a unique piecewise C2solution ui=ui(t,x)(i=1,...,N)with small piecewise C2norm on the domain

Remark 3.1.[Hidden Regularity]For the piecewiseC2solutionui=ui(t,x)(i=1,...,N)giveninLemma3.1(orLemma3.2),ifhi(t)≡0ormoregenerally,hi(t)∈C1[0,T]withsmallC1[0,T]norm on all the simple nodesEanddi1(i∈S),then there is a hidden regularity onx=d10andx=di1(i∈S)that bothu1(t,d10)andui(t,di1)(i∈S)∈C3[0,T]with smallC3norms.

Similarly,since it is assumed thatHi(t)∈C1[0,T]with smallC1norm on all the multiple nodesdi1(i∈M),there is a hidden regularity of the piecewiseC2solutionui=ui(t,x)(i=1,...,N)onx=di1(i∈M)thatui(t,di1)∈C3[0,T](i∈M)with smallC3norm.

Remark 3.2.If the types of boundary conditions on the simple nodesEanddi1(i∈S)are mixed,namely,atx=d10andx=di1(i∈S),for each indexi=1 ori∈S,the corresponding boundary condition can be taken as anyone of the following boundary conditions:

wherebi>0 is aC1function ofui,Gi=Gi(t,ui,,)is aC1function of its arguments,whilehi(t)isC2(for Dirichlet Type)orC1(for Neumann Type or Third Type)orC0(for Dynamical Type)function oft.The interface condition on multiple nodedi1(i∈M)is still given by(2.9)such that the conditions of piecewiseC2compatibility at the points(t,x)=(0,di1)(i∈M)(resp.(T,di1)(i∈M))arestillsatis fied.ThenLemma3.1andLemma 3.2 still hold,provided that the corresponding conditions ofC2compatibility at the points(0,d10)and(0,di1)(i∈S)(resp.(T,d10)and(T,di1)(i∈S))are satis fied,respectively.

It is worth mentioning that the hidden regularity can be only realized in the case that the boundary condition at simple node is taken as a dynamical boundary condition(3.14d)and the interface condition at multiple node is given as(2.9),satisfying the additional assumptions given in Remark 3.1.

4 Proof of’one-sided’exact boundary controllability

In order to prove Theorem 2.1,it suffices to prove the following:

Lemma 4.1.Under the assumptions of Theorem2.1,with the interface conditions(2.9)at all the multiple nodes and boundary condition(2.6)(h1(t)≡0or h1(t)∈C1[0,T]with small C1norm)at the starting simple node E(d10),system(2.1)admits a piecewise C2solution ui=ui(t,x)(i=1,...,N)with small piecewise C2norm on the domainwhich exactly satisfies the initial condition(2.5)and the final condition(2.12).

Proof.The proof is based on Lemma 3.1 and Lemma 3.2 and by means of the constructive method given in[4],[5]and[9].Noting(2.10),there exists anε0>0 so small that

Let

and fori∈S,let

For convenience,we suppose that there arekmultiple nodes andmsimple nodes.

(i)We first consider the forward mixed initial-boundary value problem for system(2.1)with the initial condition(2.5),the interface conditions(2.9)onkmultiple nodes,the boundary condition

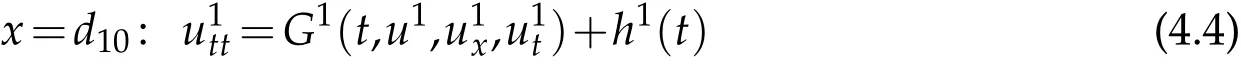
on the simple nodeE,and the following artificial boundary conditions on other(m−1)simple nodes:

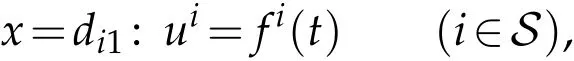
wherefi(t)(i∈S)are any givenC2functions oftwith smallC2[0,T0]norm,such that the conditions ofC2compatibility are satisfied at the point(t,x)=(0,di1)(i∈S).By Lemma 3.1 and Remark 3.2,on the domain

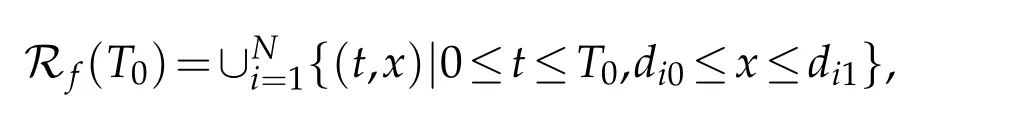
there exists a unique piecewiseC2solution uf=uf(t,x)=((t,x),...,(t,x))with small piecewiseC2norm.In particular,we have

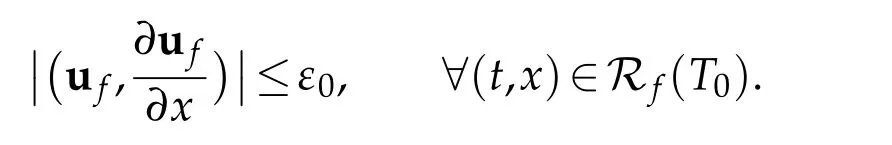
Thus,we can determine the value ofatx=d10as follows(see Figure 3(a)):

Similarly,on the multiple noded11,we can determine the corresponding value ofand(,)(j∈J1)as follows:

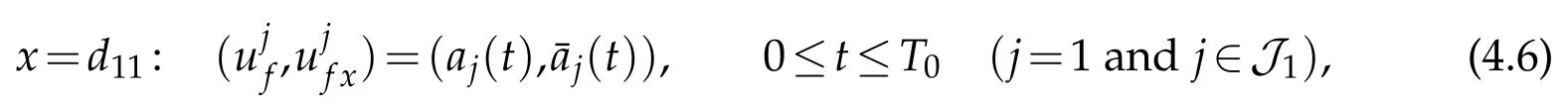
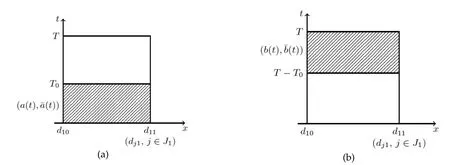
Figure 3:(a)Forward mixed problem; (b)backward mixed problem.

(ii)Similarly,we consider the backward mixed initial-boundary value problem for system(2.1)with the final condition(2.12),the interface conditions(2.9)onkmultiple nodes,the boundary condition(4.4)on the simple nodeEand the following artificial boundary conditions on other(m−1)simple nodes:

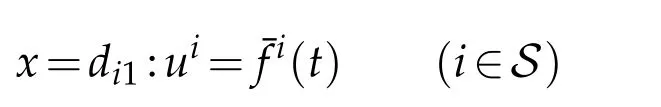
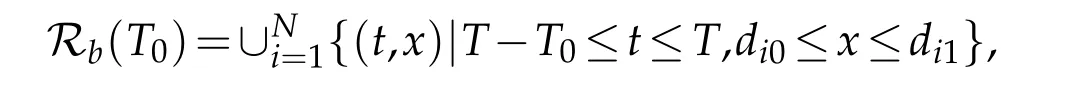
there exists a unique piecewiseC2solution ub=ub(t,x)=((t,x),...,(t,x))with small piecewiseC2norm.In particular,we have

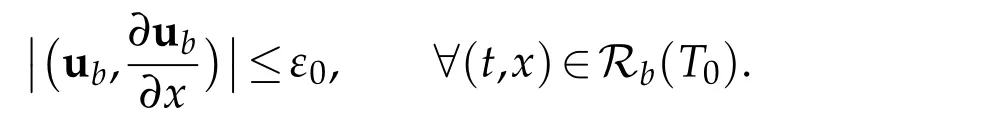
Thus,we can determine the value ofatx=d10as follows(see Figure 3(b)):

Similarly,on the multiple noded11,we can determine the corresponding value ofandas follows:

(iii)SinceRf(T0)andRb(T0)do not overlap,we want to construct(c(t),¯c(t))as a choice of the value of(u1,)atx=d10with smallC3[0,T]×C1[0,T]norm,such that

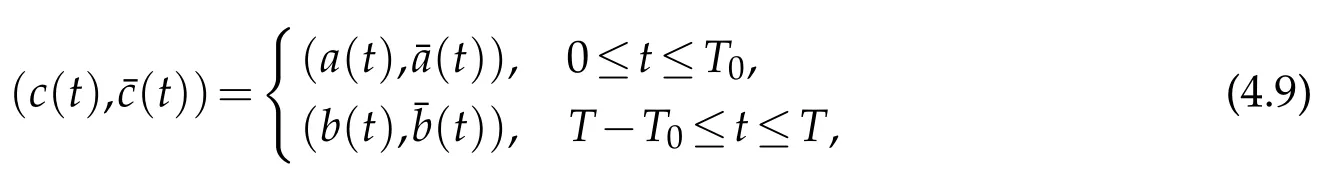
and(u1,,,)=(c(t),c0(t),c00(t),¯c(t))satisfies the boundary condition(4.4)on the whole interval[0,T]atx=d10.

To this end,we first findc(t)∈C3[0,T]with smallC3[0,T]norm,such that

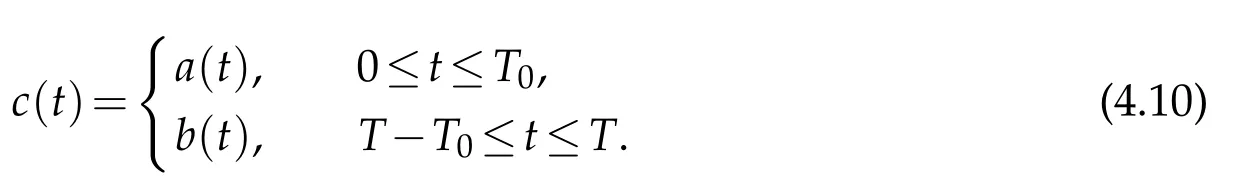
Thus,atx=d10,we have(u1,,)=(c(t),c0(t),c00(t)).

Noting(2.11),by the Implicit Function Theorem,the boundary condition(4.4)atx=d10can be uniquely rewritten on 0≤t≤Tas follows:

Let

Noting the hidden regularity given in Remark 3.1,¯c(t)∈C1[0,T]with smallC1[0,T]norm,and it is easy to see that

(iv)Noting(2.2),we now change the status oftandx,and consider the rightward mixed initial-boundary value problem(see Figure 4(a))for system(2.1)with the initial condition

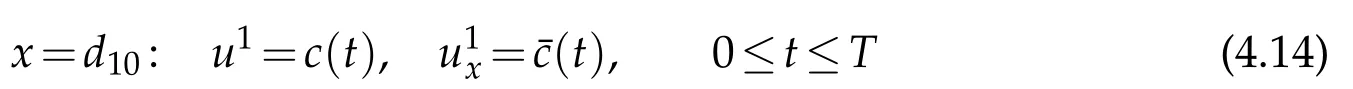
and Dirichlet boundary conditions

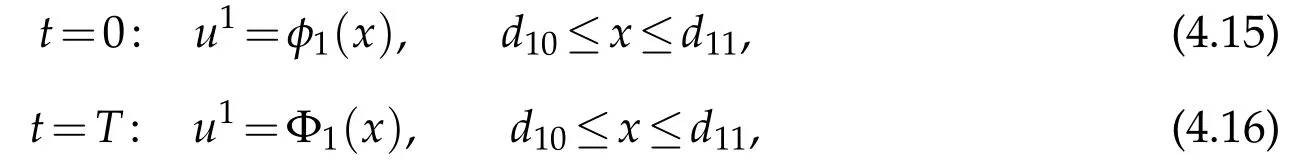
whereφ1(x)and Φ1(x)are given by(2.5)and(2.12),respectively.Obviously,the conditions ofC2compatibility at the points(t,x)=(0,d10)and(T,d10)are satisfied.Then by Lemma 3.1 and Remark 3.2,there exists a uniqueC2solutionu1=u1(t,x)with smallC2norm on the domainR1(T)={(t,x)|0≤t≤T,d10≤x≤d11}and

Figure 4:(a)Rightward mixed problem;(b)uniqueness of solutions on the shaded domain.

TheC2solutionsu1andsatisfy simultaneously the same system(2.1)(in which we takei=1),the same initial condition

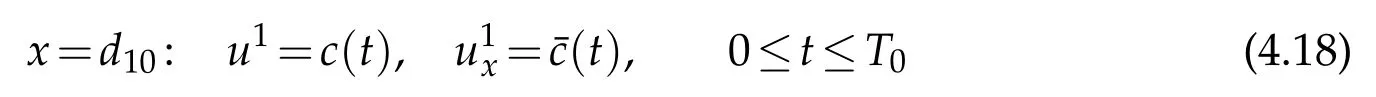
and the same boundary condition(4.15),by uniqueness ofC2solutions to the one-sided mixed initial boundary value problem(see[7]),it is easy to see thatu1on the domain(see Figure 4(b))

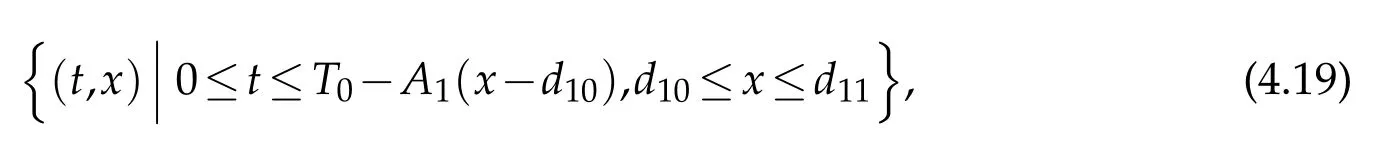
where

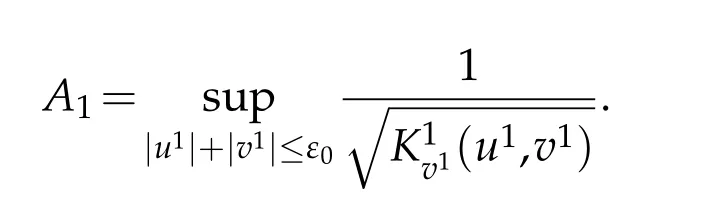
In particular,on the interval[d10,d11]on thex-axis,u1satisfies the initial condition(2.5)(in which we takei=1)and

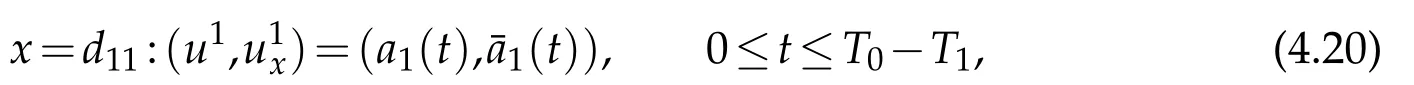
where(a1(t),(t))is given by(4.6)(in which we takej=1).

In a similar manner,we obtain thatu1on the domain(see Figure 4(b))

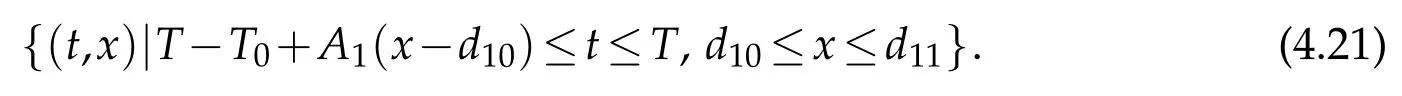
In particular,on the interval[d10,d11]on thex-axis,u1satisfies the final condition(2.12)(in which we takei=1)and

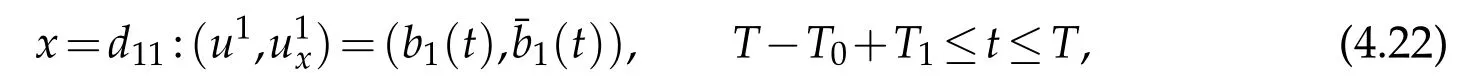
where(b1(t),(t))is given by(4.8)(in which we takej=1).

(v)On the multiple noded11,we now construct(cj(t),¯cj(t))∈C3[0,T]×C1[0,T](j=1 andj∈J1)with smallC3[0,T]×C1[0,T]norm,such that

where(aj(t),(t))and(bj(t),(t))are given by(4.6),(4.8)(in which we takej∈J1)and(4.20),(4.22)(in which we takej=1),respectively.Furthermore,(j=1 andj∈J1)should satisfy the interface conditions(2.9)atx=d11on the whole interval[0,T].

Firstly,theC2solutionu1=u1(t,x)given in step(iv)determines(c1(t),(t))as the value of(u1,)on the whole interval[0,T]atx=d11.Thus,(c1(t),(t))∈C3[0,T]×C1[0,T]with smallC3[0,T]×C1[0,T]norm,and by(4.20)and(4.22)we have

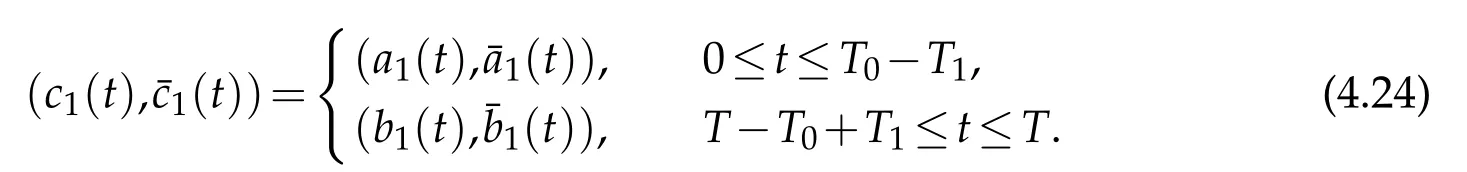
Then,by the continuity of displacements given by the interface conditions(2.9),setting

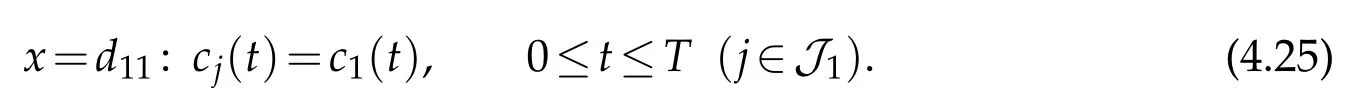
we havecj(t)∈C3[0,T]with smallC3[0,T]norm and

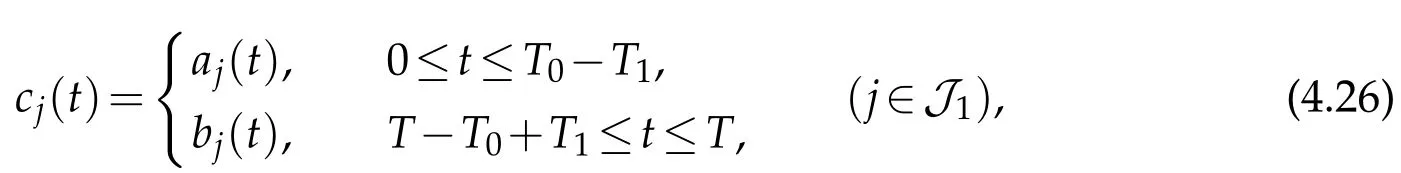
whereaj(t)andbj(t)are given by(4.6)and(4.8)(in which we takej∈J1),respectively.

Noting(2.2),in particular,there exists at least one indexj0∈J1,such that

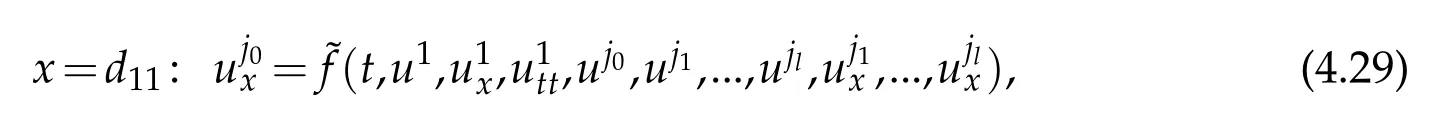
Setting

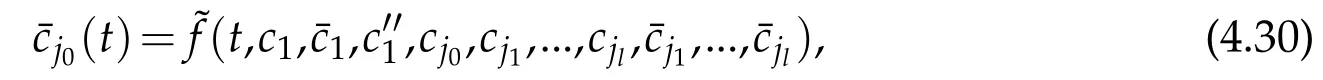
we get thatcj0(t)∈C1[0,T]with smallC1norm,and

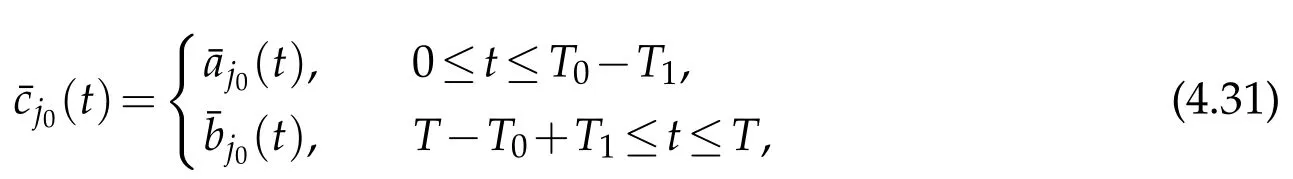
Thus,we find(cj(t),(t),(t),(t))as the value of(uj,,,)(j=1 and∈J1),satisfying the interface conditions(2.9)on the whole interval[0,T]atx=d11.

(vi) Forj∈J1(namely,dj0=d11),we can regard the nodedj0as a new starting node and do step (iv) again, namely, consider the rightward mixed initial-boundary value problem for system (2.1) with the initial condition

and Dirichlet boundary conditions

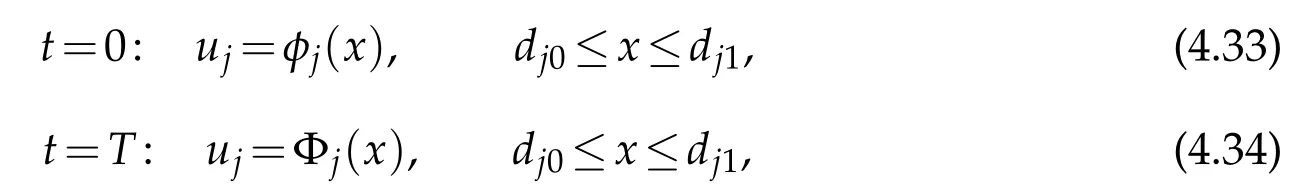
whereφj(x)and Φj(x)are given by(2.5)and(2.12)(in which we takei=j),respectively.Obviously,the conditions ofC2compatibility at the points(t,x)=(0,dj0)and(T,dj0)are satisfied,respectively.Then by Lemma 3.1 and Remark 3.2,there exists a uniqueC2solutionuj=uj(t,x)with smallC2norm on the domainRj(T)={(t,x)|0≤t≤T,dj0≤x≤dj1},and

TheC2solutionsujandujfsatisfy simultaneously the same system(2.1)(in which we takei=j),the same initial condition

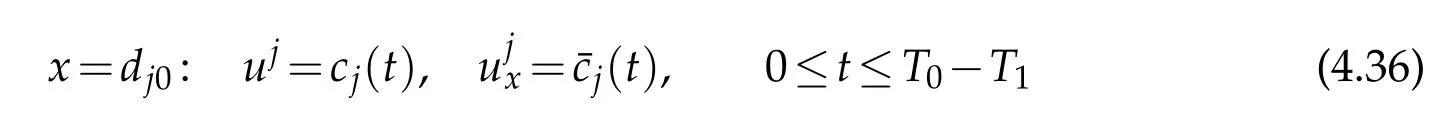
and the same boundary condition(4.33).By uniqueness ofC2solutions to the one-sided mixed initial boundary value problem(see[7]),it is easy to see thatuj≡on the domain

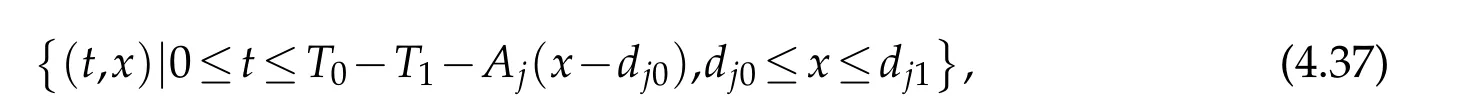
where

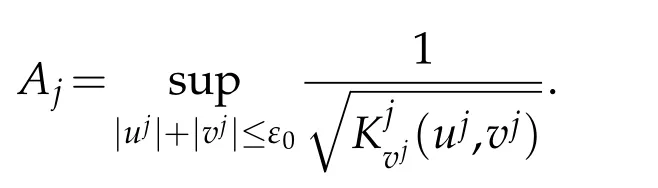
In particular,on the interval[dj0,dj1]on thex-axis,ujsatisfies the initial condition(2.5)(in which we takei=j)and

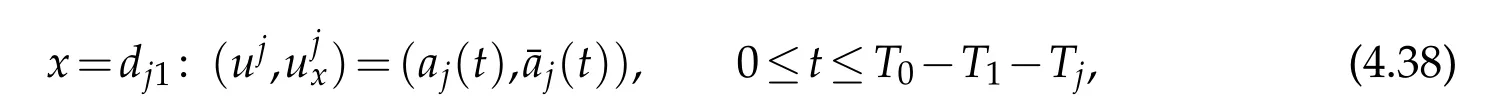
where(aj(t),(t))is given by(4.6).

Similarly,we have thatuj≡on the domain

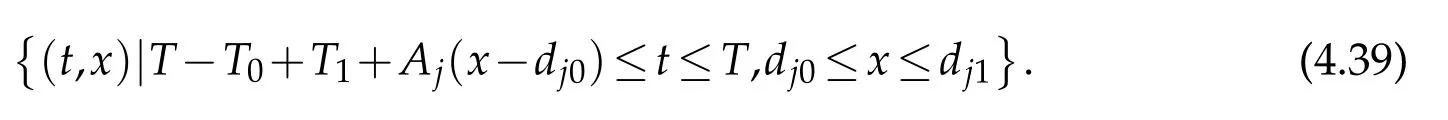
In particular,on the interval[dj0,dj1]on thex-axis,ujsatisfies the final condition(2.12)(in which we takei=j)and

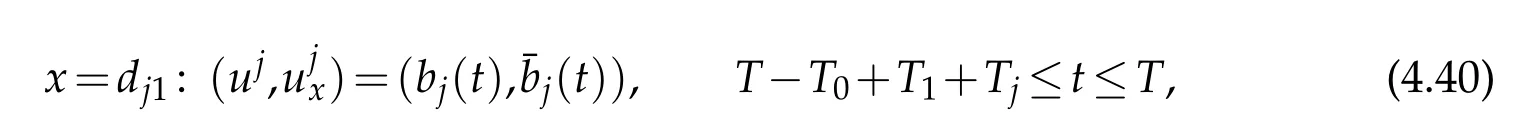
where(bj(t),(t))is given by(4.8).

The constructive process is over whenj∈S,namely,is a simple node.Otherwise,ifj∈M,namely,dj1is still a multiple node,we do step(v)again,namely,considerdk0(k∈Jj)as a new starting node and do step(iv).This process can be stopped in limited steps.

(vii)Noting the definition ofT0given by(4.2),for any giveni∈S,we have

which promises that the piecewiseC2solutionsui=ui(t,x)(i=1,...,N)obtained above satisfies

thus,u=(u1,...,uN)=(u1(t,x),...,uN(t,x))is a solution required by Lemma 4.1.

5 The proof of’two-sided’exact boundary controllability

In order to proof Theorem 2.2,it suffices to proof the following

Lemma 5.1.Under the assumptions of Theorem2.2,system(2.1)with the interface conditions(2.9)at all the multiple nodes admits a piecewise C2solution ui=ui(t,x)(i=1,...,N)with smallpiecewise C2norm on the domainwhich exactly satisfies the initial condition(2.5)and the final condition(2.15).

Proof.Based on Lemma 3.1 and Lemma 3.2,referring to and adjusting the constructive method given in[4],[5]and[9],we first find a ’longest’chain-like subnetwork and its midpointx0.Then,starting fromx0,we solve a leftward and a rightward mixed problem on the corresponding half tree-like networks,respectively,and construct a desired piecewiseC2solution.

Noting the definition of control timeTgiven by(2.13)-(2.14),there exists anε0>0 so small that

Let

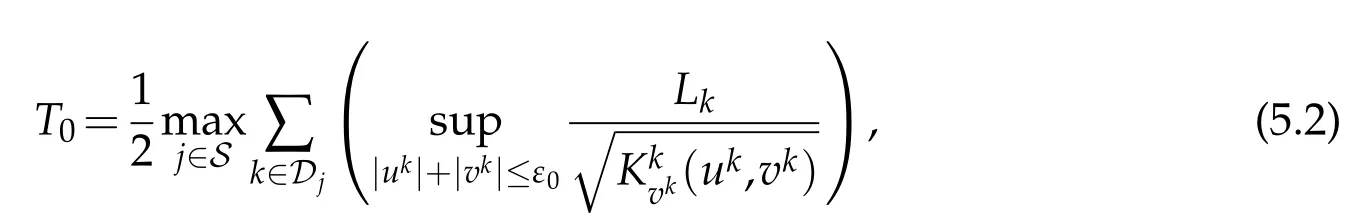
and forj∈S,let

Similarly to the proof of Lemma 4.1,we want to construct a piecewiseC2solution u=(u1,...,uN)required by Lemma 5.1 on the tree-like network.

(i)On the domain

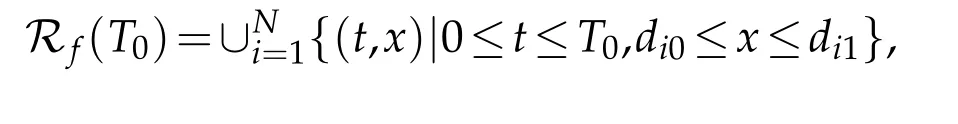
we consider the forward mixed initial-boundary value problem for system(2.1)with the initial condition(2.5),the interface conditions(2.9)onkmultiple nodes and the following artificial boundary conditions on all the simple nodes:

wheref0(t)andfi(t)(i∈S)are any givenC2functions of t with smallC2[0,T0]norms,such that the conditions ofC2compatibility are satisfied at the point(t,x)=(0,d10)and(0,di1)(i∈S),respectively.By Lemma 3.1 and Remark 3.2,there exists a unique piecewiseC2solution uf=(,...,)with small piecewiseC2norm on the domainRf(T0).

(ii)On the domain

we consider the backward mixed initial-boundary value problem for system(2.1)with the final condition(2.15),the interface condition(2.9)onkmultiple nodes and the following artificial boundary conditions on all the simple nodes:

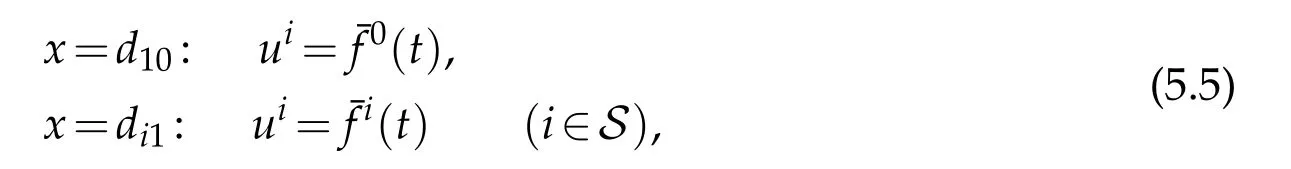
(iii)Consider one of the simple nodes on the ’longest’chain-like subnetwork as the starting nodeE(d10).Thus,there existsj0∈Ssuch that

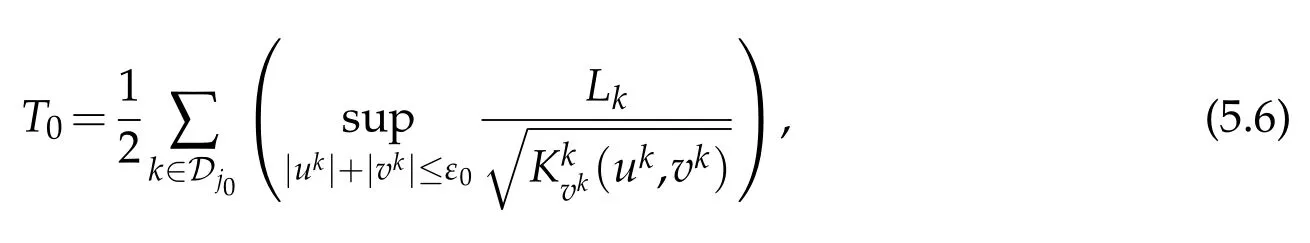
andDj0is a ’longest’chain-like subnetwork on the tree-like network.

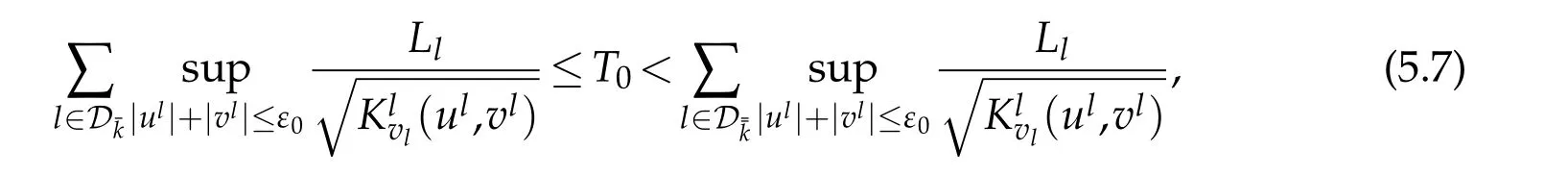
where(resp.)stands for the set of indiceslof stringSl,which are contained in the chain-like network betweenEand node(resp.).Hence,we can findx0∈[,)such that

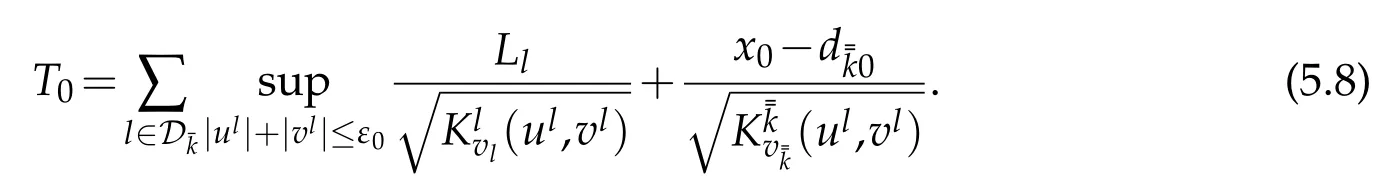
Thus,We can regardx0as a ’midpoint’of this’longest’chain-like subnetwork(see Figure 5).

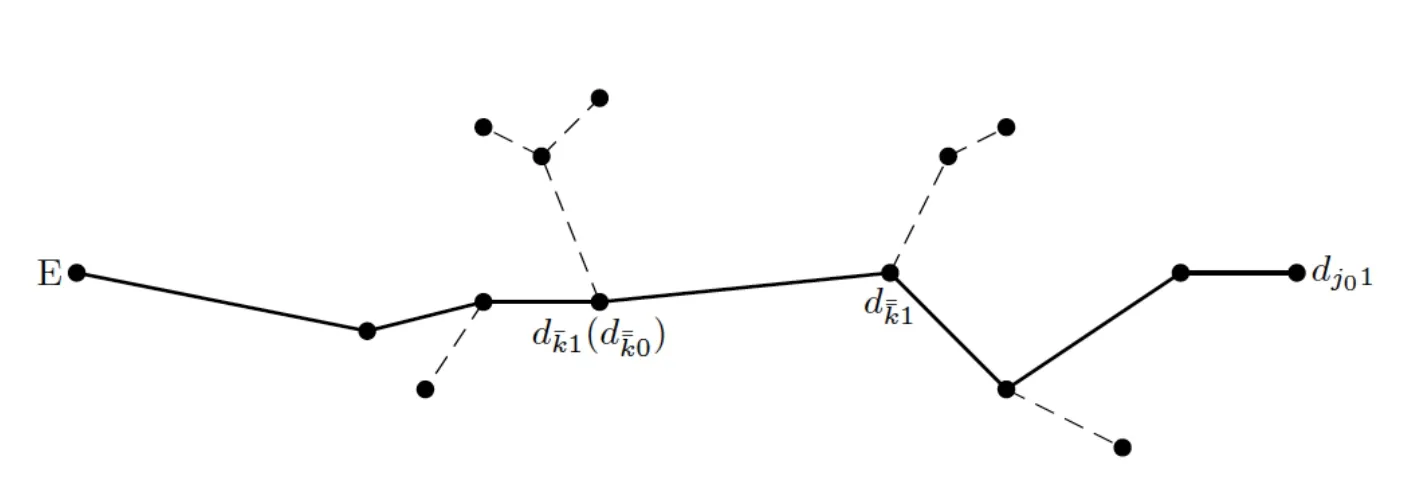
Figure 5:The ’longest’chain-like subnetwork.

The following discussion will be divided into two cases.

We first discuss the case that0,namely,x0is not a node on the tree-like network.

(iv)Thus,respectively,we can determine the value ofandatx=x0by the results given in(i)and(ii)as follows:

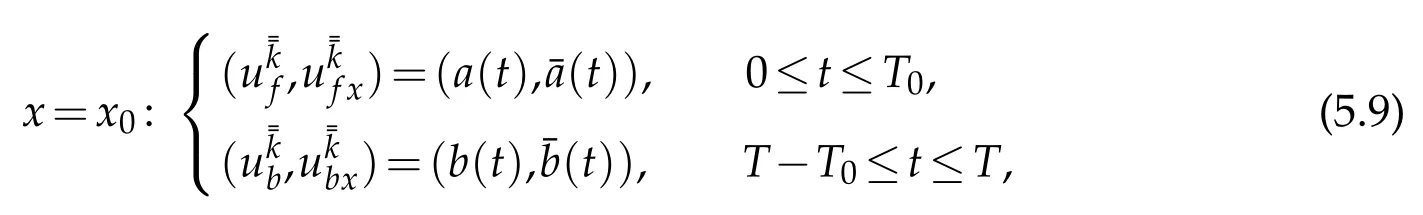
Noting(5.1)and(5.2),we can find(c(t),(t))with smallnorm,being the value of(,)on the whole time interval[0,T]atx=x0,and

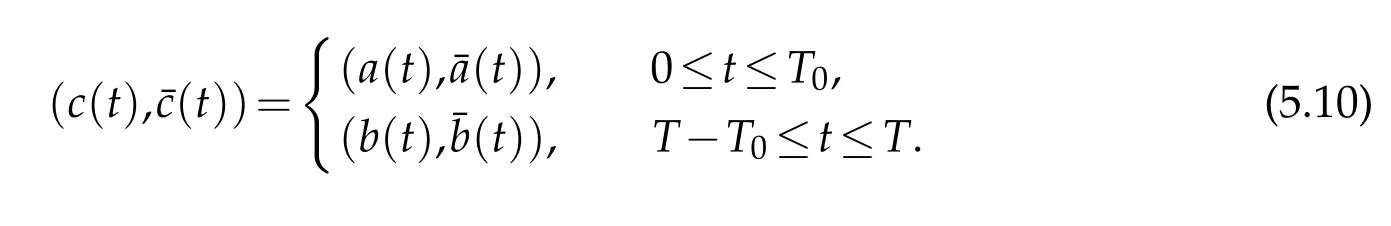
Noting(2.2),we now change the status oftandx,and consider the leftward mixed initial-boundary value problem(see Figure 6(a))for system(2.1)with the initial condition

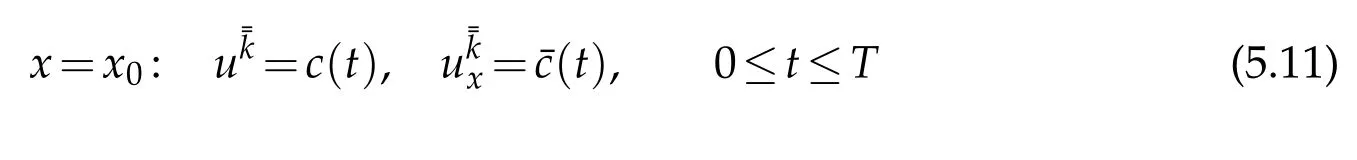
and Dirichlet boundary conditions

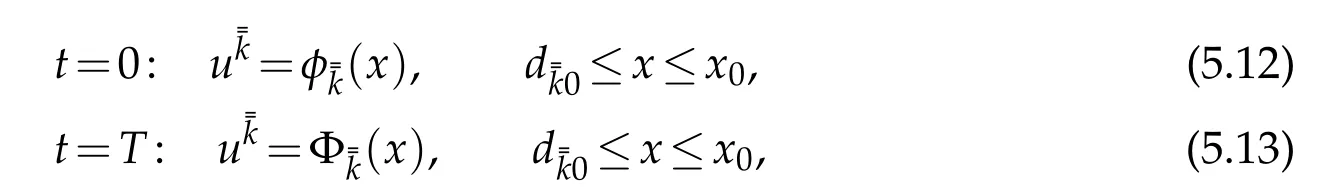
where(x)and(x)are given by(2.5)and(2.15),respectively.Obviously,the conditions ofC2compatibility at the points(t,x)=(0,x0)and(T,x0)are satisfied.Then there exists a uniqueC2solution=(t,x)with smallC2norm on the domain(T)={(t,x)|0≤t≤T≤x≤x0}and

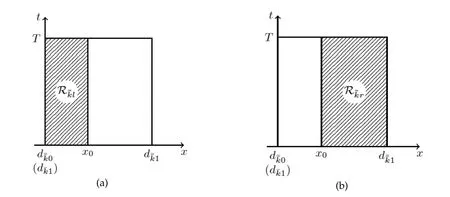
Figure 6:(a)Leftward mixed problem;(b)rightward mixed problem.

Similarly,for the rightward mixed initial-boundary value problem(see Figure 6(b))for system(2.1)with the initial condition(5.11)and Dirichlet boundary conditions

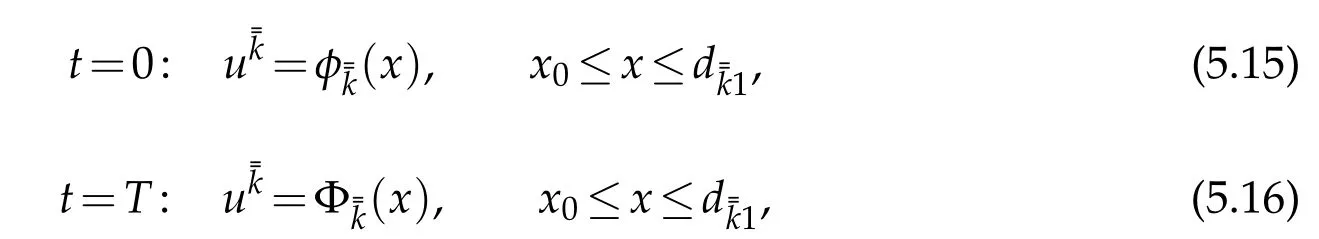
there exists a uniqueC2solution=(t,x)with smallC2norm on the domain(T)={(t,x)|0≤t≤T,x0and

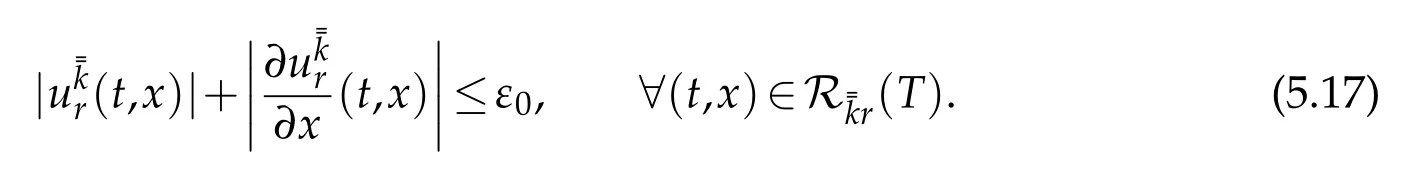
Let

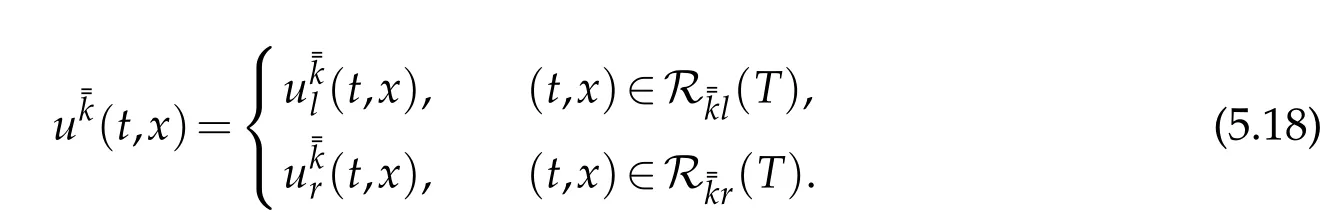
Obviously,(t,x)is aC2solution on the domain(T)={(t,x)|0≤t≤T.

TheC2solutions(resp.)andsatisfy simultaneously the same system(2.1)(in which we takei=),the same initial condition(5.11)and the same boundary condition(5.12)(resp.(5.15)),by uniqueness ofC2solutions to the one-sided mixed initial boundary value problem(see[7]),on the trapezoidal area(see Figure 7)

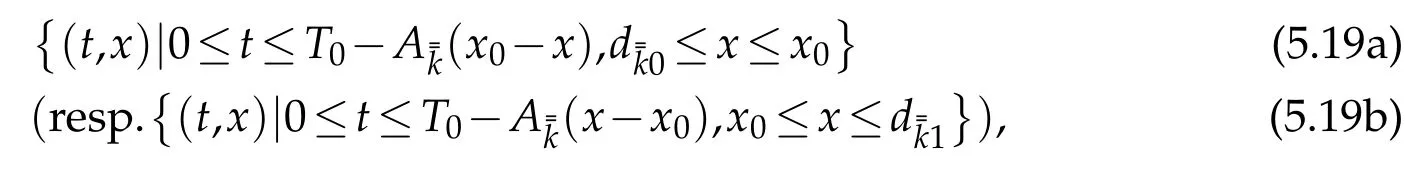
where

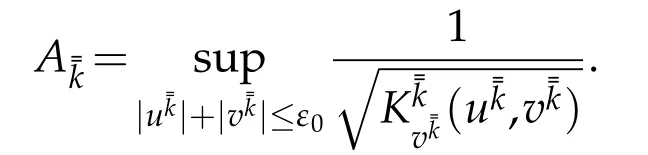
In particular,on the interval[,]on thex-axis,satisfies the initial condition(2.5)(in which we takei=),and on two ends of stringwe have

where((t),(t))and((t),(t))are given by the forward solution(,)obtained in(i).

Similarly,we obtain thatalso satisfies the final condition(2.15)(in which we takei=),and on two ends of stringwe have

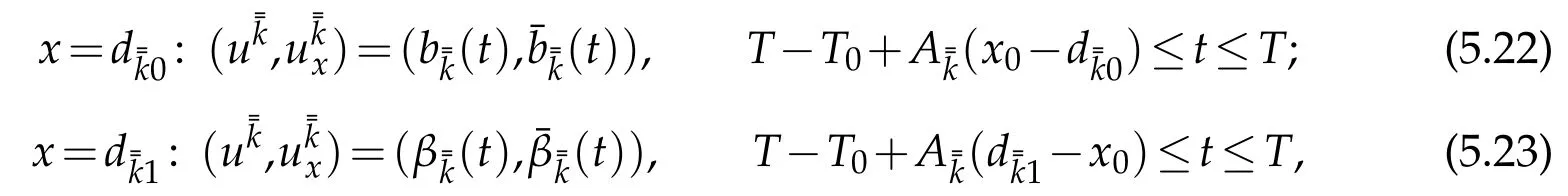
where((t)(t))and((t),(t))are given by the backward solution(,)obtained in(ii).

(v)Ifis a simple node,the rightward constructive procedure is over.Otherwise,on the multiple node,in a similar way as(v)in the proof of Lemma 4.1,we can find(cl(t),(t))∈C3[0,T]×C1[0,T](l=and)with smallC3[0,T]×C1[0,T]norm,being the value of(ul,)(l=and),and forl=and,

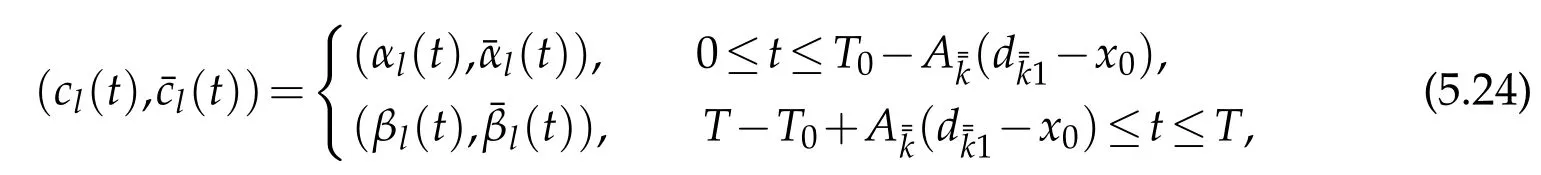
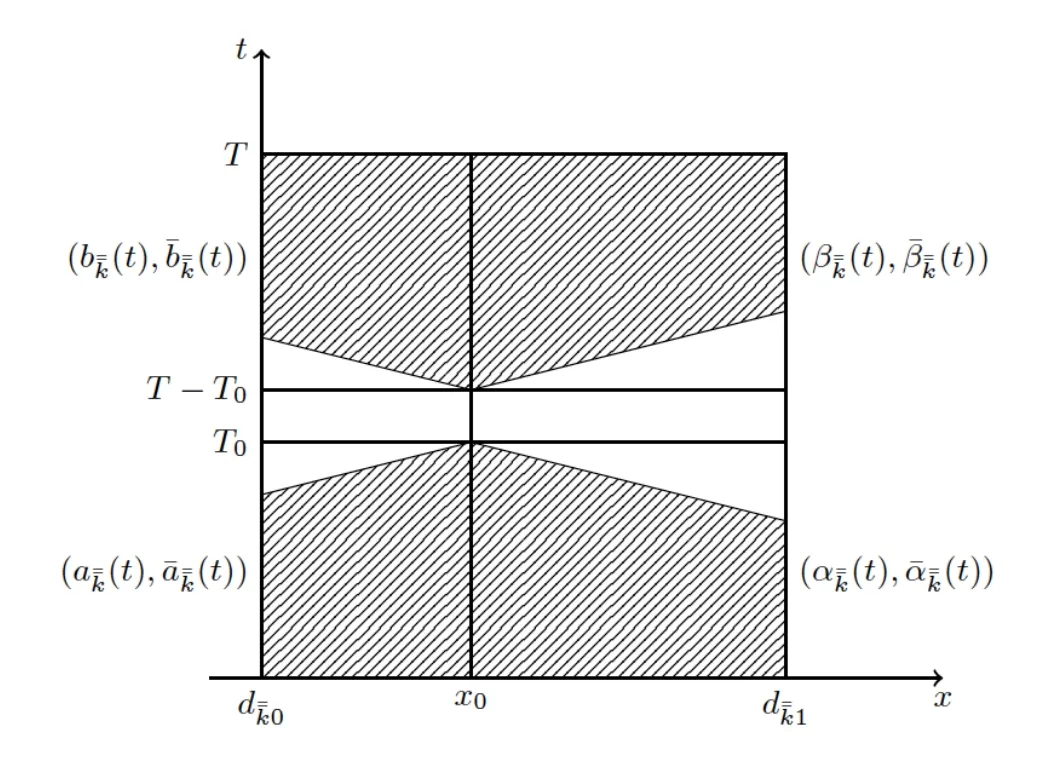
Figure 7:Uniqueness of solutions on the shaded domain.

where(αl(t),(t))(l∈J¯k)and(βl(t),(t))()are determined by the forward solution(,)and the backward solution(,)obtained in(i)and(ii),respectively.Thussatisfies the interface conditions(2.9)on the whole interval[0,T].

For,we considerdl0as a starting node and solve the rightward mixed initialboundary value problem for system(2.1)with the initial condition

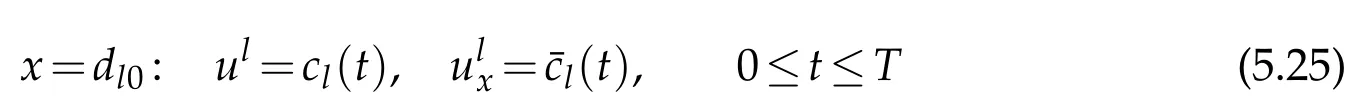
and Dirichlet boundary conditions

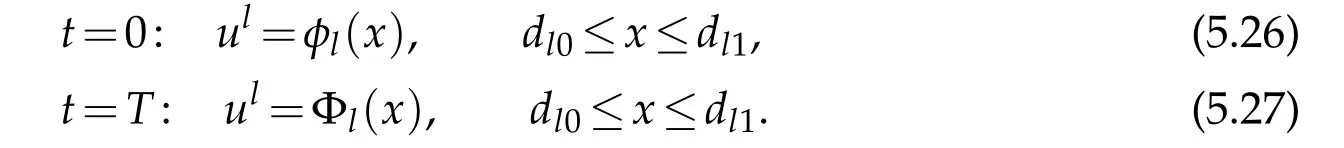
There exists a uniqueC2solutionul=ul(t,x)with smallC2norm on the domainRl(T)={(t,x)|0≤t≤T,dl0≤x≤dl1}and

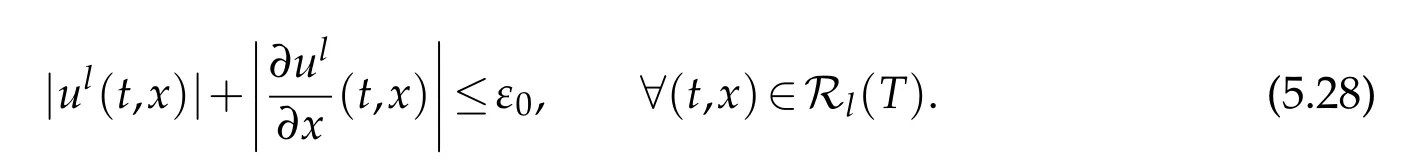
By uniqueness ofC2solutions to the one-sided mixed initial-boundary value problem(see[7]),it is easy to prove thatul=ul(t,x)satisfies the initial condition(2.5)(in which we takei=l)and the final condition(in which we takei=l),and on nodedl1we have

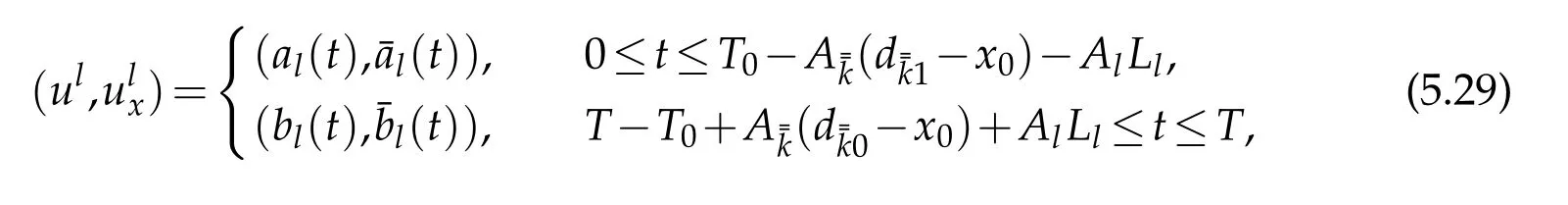
where(al(t)(t))and(bl(t),(t))are given by the forward solution(,)and the backward solution(,)obtained in(i)and(ii),respectively.

(vi)The rightward constructive procedure is over whendl1is a simple node.Otherwise,consideringdl1as a starting node and do the constructive process above again,it is easy to see that we can continue this rightward constructive procedure on the right half tree-like network.

Whendj1is a node on the right half of the tree-like network,there is a unique chainlike subnetwork connecting pointx=x0and nodedj1.LetDx0,jstand for the set of indiceskof all nodesdk0contained in this subnetwork.Noting(5.1),(5.2)and the definition ofx0given by(5.8),we have

Thus,for any givenk1,k2∈Dx0,jsatisfyingdk11=dk20,we haveuk2(resp.uk2)on the the trapezoidal area(see Figure 8)

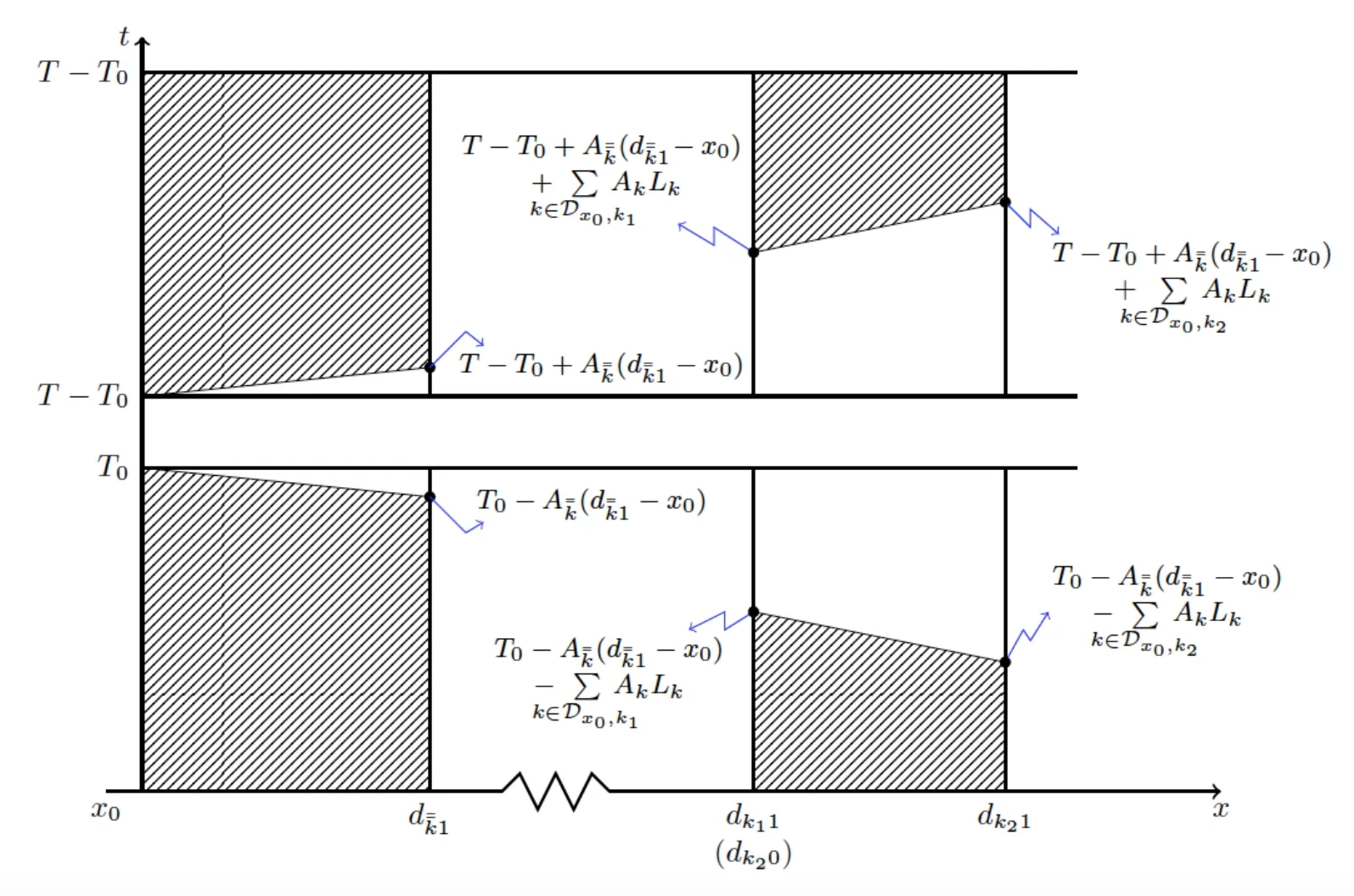
Figure 8:The rightward procedure and uniqueness of solutions on the shaded domain.

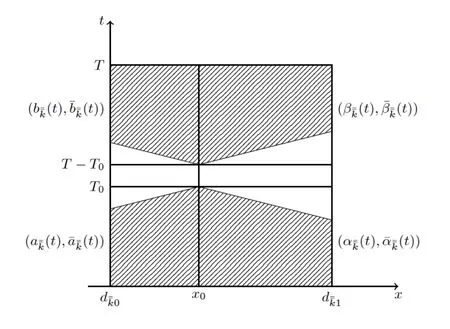
Figure 9:The case that x0is exactly a multiple node.

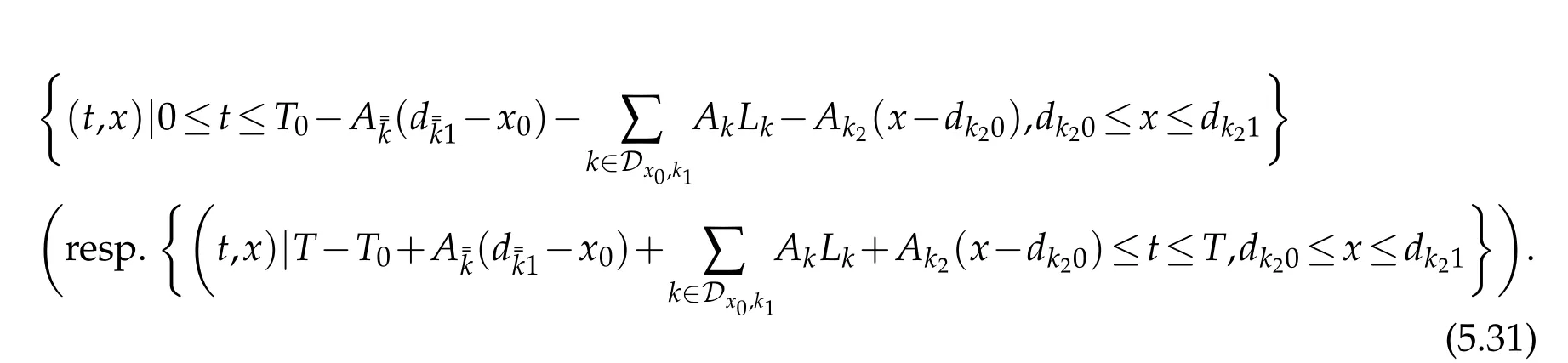
Thus,the piecewiseC2solutionuk(k∈Dx0,j)constructed above satisfies simultaneously the initial condition(2.5)and the final condition(2.15).

(vii) Similarly to the rightward constructive procedure shown in step(v)and(vi),starting fromx0,we can finish the leftward constructive procedure on the left half of the tree-like network by steps.

We now discuss the case thatx0=(x0=),namely,x0is exactly the multiple nodeon the network(see Figure 9).

In this case,by steps(i)and(ii),we can determine the value of(,),(,)andatx=x0as follows:

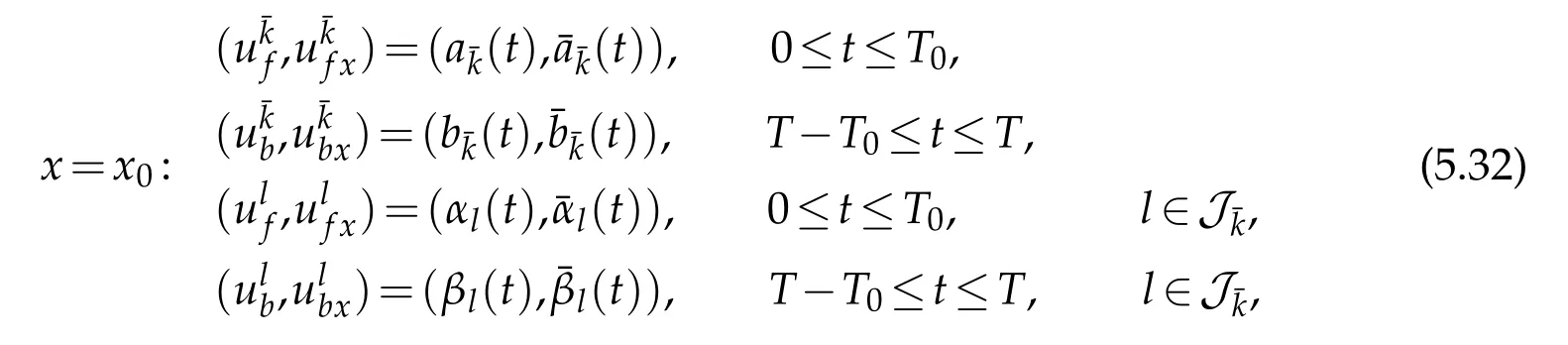
and,by the hidden regularity on the multiple nodes,

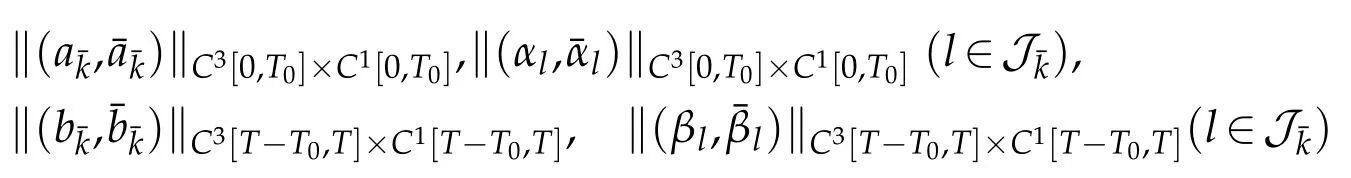
are all small enough.Furthermore,by the interface conditions(2.9)(in which we takei=),we have

Noting(5.1)and(5.2),we can find(c(t),¯c(t))with smallnorm,being the value of(,)on the whole time interval[0,T]atx=x0,such that

Similar to the proof in(v),we can findwith small()norm,being the value of(ul,)()on the whole time interval[0,T]atx=x0,such that

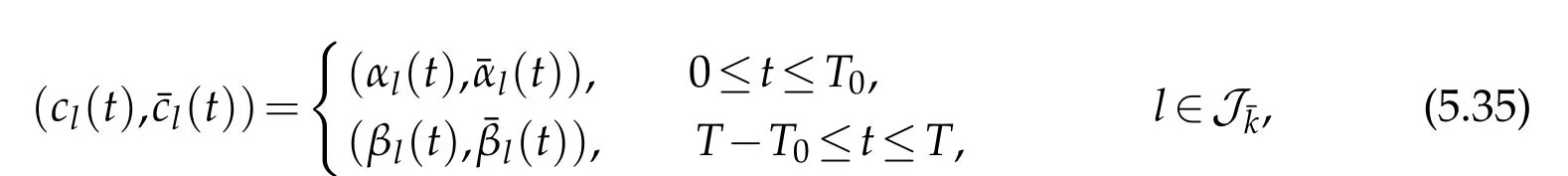
and((t),(t)),(cl(t)(t))()satisfy the interface conditions(2.9)(in which we takei=¯k)on the whole interval[0,T]atx=(x=x0).

Starting fromx=x0(x=),similarly to(v)and(vi),we can finish the leftward and rightward constructive procedure on the corresponding left and right half of tree-like network.Thus,we get a piecewiseC2solution u=(u1,...,uN)with small piecewiseC2norm.

(vii)Noting the setting ofT0given by(4.2),for any giveni∈S,we have

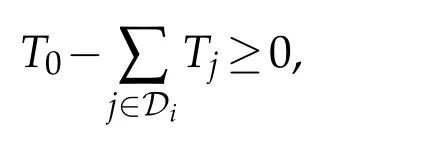
which promises that the piecewiseC2solutionsui=ui(t,x)(i=1,...,N)obtained above satisfy

then,u=(u1,...,uN)=(u1(t,x),...,uN(t,x))satisfies the initial condition(2.5)and the final condition(2.12).Consequently,this solution meets with all the requirements given in Lemma 5.1.

Acknowledgments

The first author was supported by the National Basic Research Program of China(No.2013CB834100),and the National Natural Science Foundation of China(No.11121101).The second author was supported by the Original Research Fund of Peking University.