多舰协同超视距定位及其误差分析∗

王玉梅 张殿友 徐海洋

（1.江苏科技大学 镇江 212003）（2.中国船舶重工集团第七二三研究所 扬州 225100）

1 引言

在复杂的电磁环境下，多舰协同测向定位是较常用的一种多站协同定位方式，相对于两站定位，多舰协同测向定位具有更高的定位精度以及更稳定的性能，不会因某个站失效或者受到干扰而丧失定位功能［1］。在已有的多站定位方法中多是最小二乘法及其改进算法［2～4］。研究经验表明，目标到参与定位的舰艇的相对位置对定位精度具有很大影响，若对所有组合的定位数据采用相同的处理方式，得到的最终定位结果的误差将会很大。另外，由于超视距定位作用目标距离远，导致不合理布站引起的定位误差相比于视距测向定位要大很多，因此本文先通过设定门限值，对理论定位误差大于门限的定位点进行剔除，然后再利用每个组合的圆概率误差对结果加权融合，求得优化定位结果。

为了提高定位精度，需要合理配置舰艇数量、舰艇间距及编队队形。已有研究人员对两个侦察站布站［5～7］对定位误差的影响进行了研究，提出了多个侦察站布站优化方案［8～10］。本文针对协同实现超视距定位的舰艇编队，对多种布站情况下采用测向方位面定位算法［11］的定位误差分布进行了仿真，为进行超视距侦察定位的舰艇编队的布站提供了理论指导。

2 定位点加权融合

加权平均是一种实用的数据求精的计算方法［12］，对多个侦察站测得的同一目标的测向数据两两组合采用测向方位面算法分别对目标进行定位，由于定位精度与目标相对侦察站的位置是密切相关的，每个组合具有不同的定位精度。因此，考虑根据圆概率误差对所有定位点进行加权融合来求取目标最终定位位置。

假设有N个舰载侦察站S1～SN对同一个目标进行定位，采用两两组合定位能得到n=个定位点，采用文献［11］中提出的测向方位面定位算法进行定位可得n个目标位置。设每种组合求得的目标经纬度分别为 Lti,j，Bti,j（i=1,2,…N，j=1,2,…N ，且 j≠i）。

2.1 权值计算

测向方位面定位算法的圆概率误差由下式计算［11］：

其中a为地球椭球的长半轴，e为第一偏心率，在WGS-84椭球体下，a=6378137m，e2=0.006 694 379 901 3 ，E[(ΔBt)2]和 E[(ΔLt)2]的具体计算过程见参考文献［11］。

根据式（1），圆概率误差CEP可以在经度和纬度上分为两个分量，定位精度与圆概率误差呈反比，令纬度上的权分量为

2.2 仿真分析

影响定位误差的因素主要有侦察站的测向精度、站址误差以及布站情况。设侦察站S1～S5的测向误差分别为1°、0.8°、1°、0.8°和1.2°，不考虑站址误差，分别采用直接平均和加权融合算法进行1000次蒙特卡罗仿真，得出的定位点如图1和图2所示。

比较图1和图2，直接平均法计算得到的目标位置非常发散，甚至存在定位结果出错的情况。而采用加权融合法得到的目标位置分布更集中，但仍存在少量的点偏离实际位置较远。根据1000次仿真数据计算得到平均值法得到的目标位置到目标真实位置的平均距离约为138.25km，而加权算法约为38.8km。因此，多舰协同超视距定位不能直接使用平均值法求取最终定位结果，而采用加权融合的方法能够有效地提高目标定位精度。

3 大误差定位点剔除

根据上一小节的仿真分析，在利用圆概率误差进行加权融合处理后得到的定位点仍然存在受大误差定位点影响而大幅度偏离目标真实位置的情况。因此，为防止高精度定位结果被平均而导致最终的定位精度降低，考虑设置一个圆概率误差的门限值ηcep，先将误差大于门限值的定位点剔除，具体步骤如下：

步骤1：根据式（1）计算出所有组合定位的圆概率误差：

其中：i=1,2,…N ，j=1,2,…N ，且 j≠i；

步骤3：若圆概率误差CEPi,j大于门限值ηcep，则将对应的i和 j组合的定位结果(Lti,j,Bti,j)剔除。

如图3所示进行布站，设侦察站测向误差均为1°，站址误差20m，采用上述方法进行10000次蒙特卡罗仿真，统计出了各侦察站组合得到的定位点被剔除的概率，结果见表1。

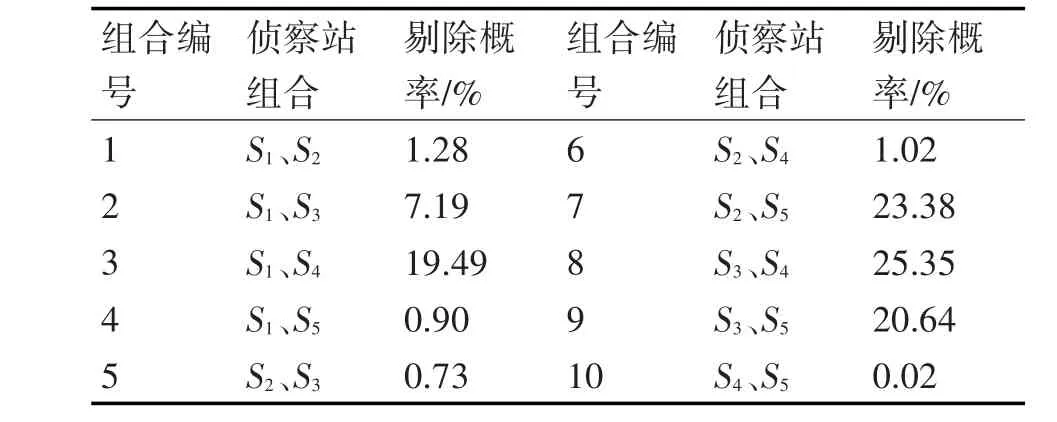
表1 不同侦察站组合定位结果被剔除的概率

根据表1，编号3、7、8和9的组合得到的定位结果被剔除的概率较大，结合图3中所有侦察站与目标的相对位置关系，这四个组合中目标均位于偏离两侦察站基线中垂线位置，这与测向方位面算法误差分布的理论分析相符，因此采用该方法能够对较大误差定位点进行有效剔除。

4 定位误差仿真分析

为了方便表述，将直接求所有定位点的平均值的方法记为方法1，剔除了误差较大的定位点之后采取平均值法记为方法2，直接使用加权平均的方法记为方法3，在剔除误差较大的定位点之后再采用加权平均的方法记为方法4。

按照图3进行布站，设置侦察站S1～S5的站址误差为 20m，测向误差分别为 1°、0.8°、1°、0.8°和1.2°。采用方法2和方法4进行1000次蒙特卡罗仿真，仿真结果如图4和图5所示。

比较图1、图2、图4和图5，方法1得到的定位点最为分散，方法2得到的定位点相对比较集中，方法3得到的定位点总体较为集中，但存在极少数偏离实际位置较远的情况，方法4得到的定位点最为集中，且不存在偶然偏离的情况。因此在这四种方法中，方法4的定位结果误差较小。

假设有5个侦察站S1～S5，设置侦察站站址误差20m，使用侦察站S1～S5中的2～5个站的不同组合采用方法3进行定位，进行1000次蒙特卡罗仿真得到最终定位结果与目标真实位置的平均距离见表2。

根据表2，比较2站和3站或者4站和5站的组合，发现增加侦察站的数量并不一定能够提高定位精度。在两站定位中，S4和S5定位得到的结果最接近目标的真实位置，因此含有S4和S5的组合得到的结果在相同数量侦察站的情况下效果最好。并且，在此次仿真中，所有含有S4和S5的组合得到的最终个结果与目标的平均距离相差无几，而不含S4和S5的多站组合的定位误差反而大于S4和S5的定位结果。因此，若要通过采用增加侦察站数量来提高定位精度需要研究多站在不同布站情况下的误差分布。

表2 不同侦察站组合采用方法3得到的最终定位结果到目标真实位置的平均距离距离

5 多舰布站方案分析

设置目标位于经度115°～125°、纬度5°～15°的栅格内，各侦察站测向误差均为1°。

两个侦察站时，侦察站按直线布站，只有基线长度可变。下面对基线长度为L=50km和L=100km时的两站测向方位面定位算法的GDOP分布进行仿真，结果如图6所示。图中的小三角形为侦察站所在位置，显示的定位误差值的单位为km。比较图 7（a）和（b），基线长度由50km增加到100km后，GDOP分布变得更加稀疏，即对同一目标进行定位时，两侦察站基线越长的定位精度越高。

5.1 三站协同定位误差分布

采用三个侦察站定位，两站最小基线长度为L=50km，对采用直线和正三角形布站的三站测向方位面定位算法的GDOP分布进行仿真，结果如图7和图8所示。

比较图7和图 6（b），三个站直线分布在L=100km的两站的基线中间增加了一个侦察站，而图7和图6（b）具有相同的误差分布，因此在侦察站间的基线上增加侦察站数量不能减小定位误差。

比较图7和图8，在相同的精度要求下，三站直线分布时在垂直基线的方向上的误差分布更加稀疏，适合于对特定方向定位，而等边三角形分布能够对整个区域进行定位且没有定位盲区，适合于对广阔的海域进行探测。

5.2 四站协同定位误差分布

采用四个侦察站定位，两站最小基线长度为L=50km，对采用直线和正三角形布站的三站测向方位面定位算法的GDOP分布进行仿真，结果如图9～图12所示。

比较图7和图9，相对于三站直线分布，四站直线分布的最长基线长度增加了50km，因此定位精度更高。

比较图8和图12，采用正多边形分布时，在相邻两个侦察站基线长度相同的情况下，用于定位的侦察站数量越多，系统的定位误差越小，且定位误差在各方向上的分布更加均匀。

比较图10、图11和图12，三种布站情况下得到的定位误差在各个方向上的分布非常均匀，相较于三角形和星形布站，正方形布站在各个方向上的误差分布更加均匀。在相同定位精度要求下，星形和正方形布站在探测距离上要优于等边三角形布站。

6 结语

本文主要研究了多舰协同超视距定位方法并对其定位误差进行了分析，先通过设定门限值的方法，对理论定位误差大于门限的定位点进行剔除，然后再利用每个组合的圆概率误差对结果加权求解最终定位结果。最后通过仿真分析，验证了采用上述方法能够有效避免由不合理布站得到的定位点对协同定位结果的影响。

通过比较不同侦察站数量以及不同组合的定位结果，发现并不是用于定位的侦察站数量越多定位的精度就越高，定位精度还与这些侦察站的布站方式密切相关。通过对多种布站情况下采用测向方位面定位算法的定位误差分布进行了仿真，发现相同侦察站数量下，采用直线布站具有较好的方向性，即在垂直于基线方向上具有较高的定位精度，采用正多边形布站各方向上误差分布较为均匀，且侦察站数量越多越均匀。据此，可以根据不同的作战目的，对舰艇数量、间距及编队队形的配置进行合理的调整。