The Study of“Coulomb Asymmetry” in an Elliptically Polarized Laser Field∗

Kai-Yun Huang(黄凯云), Yu Hou(侯宇),Yu-Hua Zhu(祝玉华),Hui-Jing Yang(杨会静),and Xi-Dong Yang(杨希东)

Department of Physics,Tangshan Normal University,Tangshan 063000,China

AbstractDue to the effect of Coulomb potential,the angular distribution of electron ionized in an elliptically polarizedfield presents an asymmetric structure,which is called “Coulomb asymmetry”.In this paper,we study how to modulate the asymmetric degree of the electron angular distribution by using a semi-classical simplified tunneling model.It is found that the asymmetric structure is easily affected by three parameters:the ionization potential,the laser ellipticity,and the laser wavelength.However,the laser intensity has little effect on the asymmetric structure.To explain these phenomena we have derived an analytical formula,which clearly demonstrates the relationship between the asymmetric degree and these parameters.Moreover,we find that in elliptically polarized laser field only those electrons that are released in a certain narrow window of initial field phase are greatly effected by the Coulomb potential and play the key role in the formation of asymmetric structure.This study provides some reference values in the development of attoclock technique,which can be used to probe the tunneling process.

Key words:Coulomb asymmetry,semiclassical model,Coulomb correction,tunneling

1 Introduction

In strong-field laser physics,the Coulomb interaction between the parent ion and the launched electron has attracted a lot of interests.[1−5]Since the Coulomb potential is a long-range potential,performing an obvious pull-back force on the escaped electron far away from the nucleus,the trajectories of the returning electron in linearly polarized laser field present a converging form towards the core.This physical picture is vividly called“Coulomb focusing”.[6−7]In an elliptically polarized field,the photoelectron angular distribution is predicted to be symmetric about both main axes of the polarization ellipse by the strong-field approximation theory(SFA),which neglects the effect of the binding potential.[8]However,the experimentally observed distributions of electron are asymmetric in any half of the polarization plane.This asymmetrical structure results from the atomic potential and researchers name this phenomenon “Coulomb asymmetry”.[9−12]

The structure of“Coulomb asymmetry” has an important application in attosecond physics.For example,the heart of attoclock technique,which is used to probe the tunnel ionization process depends on the accurate measurement of the angular distribution in elliptically polarized laser field.[13−17]Now it is clearly known that the angular distribution is asymmetric in the elliptical polarization plane and is deeply understood that this asymmetry is caused by the Coulomb attraction between the liberated electron and the parent ion.But researches on how to modulate this degree of asymmetry are rarely conducted.In this paper,using a simplified semi-classical tunneling model,we study the influence of ionization potential,laser intensity,laser ellipticity and the laser wavelength on the structure of“Coulomb asymmetry”.

The semiclassical tunneling model is an effective tool to resolve problems in strong filed ionization.This model has successfully explained many experimental results by connecting together the quantum tunneling process and the classical orbit motion of electron.[18−20]During calculation,we employ a simplified trajectory of electron provided by Ref.[9]to replace the electron’s real motion,which has greatly improved the computing efficiency.The simplified model can reproduce the angular distribution of electron observed for neon in experiment,therefore it can be used to study the modulation of“Coulomb asymmetry”.It is found that the greater the ionization potential as well as the laser ellipticity and wavelength is,the smaller the offset angle,which is used to represent the degree of asymmetry,becomes.However,the change of laser intensity has little effect on the asymmetric structure.These phenomena can be explained by a derived analytical formula.In addition,we find that the Coulomb potential only has a great influence on the electrons that are released in a certain narrow window of initial field phase rather than on all of the electrons with arbitrary initial conditions.

Our paper is organized as follows.In Sec.2,we presentour semiclassical model and describe the dynamics of the ionized electron in combined electric and Coulomb field.

2 Model and Method

The elliptically polarized laser pulse propagating in the z-direction is given by:

where I and ω are the intensity and frequency of the laserfield,respectively.χ is the ellipticity(the major axis of polarization is along the x-direction),and f(t)is the halftrapezoidal pulse envelope,constant for the first seven cycles and ramped o ffwithin the last three cycles.For manycycle pulse,the carrier envelope phase ϕcis approximately set to be zero.

Fig.1(Color online)Schematic of Coulomb energy barrier modified by an instantaneous laser electric field.The green lines on the x-y plane are the two-dimensional projection of the potential energy.

In the semi-classical tunneling ionization model,since the laser frequency is much less than the frequency of electron moving around the nucleus,at any instant the laserfield can be approximately treated as an instantaneous static electric field.In this situation,the Coulomb potential along the opposite direction of laser polarization is deeply suppressed and an effective potential barrier is formed,as seen in Fig.1.Then the electron can be ionized through the way of tunneling across the barrier.Assuming that tunneling occurs at the instant of t0,the magnitude of the electric field strength at this moment is

And the ionization rate is[21−24]In these equations,Ipis the ionization potential and v⊥is the initial transverse velocity of electron after tunneling.The initial velocity parallel to the electric field after tunneling is zero.From the above analysis,we can see that the ionization step is determined by quantum tunneling while the subsequent propagation of electron can be solved classically with the Newton’s equation of motion.According to the theory of Laudau,[25]the initial positions for the electron are x0= −(η0/2)cosθ,y0= −(η0/2)sinθ,z0=0,whereand θ is the angle made by the electric field vector with the positive x-axis at tunneling.For the initial velocities,vx0=−v⊥sinβ sinθ,vy0=v⊥sinβ cosθ,vz0= −v⊥cosβ,where β is the angle between v⊥and the positive z-axis.

The motion of electron in the combined Coulomb and laser field has no analytical solutions and the number of electron trajectories that we have traced is quite large(about 5×106trajectories),therefore the simulated calculation is very time-consuming.In order to solve this problem,we employ a smart approximation from Ref.[9]The final momentum of electron can be divided into two parts:

where∆t is a small interval of time and the second termdt is approximately equal to zero.During the short time interval(t0∼ t0+∆t),the electron can be considered as moving in a straight line and with a constant acceleration induced by the electric field at tunnelin(t0).In this way,we get the momentum contributed by the Coulomb potential:

use the above corrected semiclassical model to study the electron angular distribution in elliptically polarized field.

3 Results and Discussions

The photoelectron angular distribution for neon is presented in Fig.2.In this figure,the green solid line is the result obtained in pure laser field.Under this condition,the angular distribution is symmetric with respect to both main axes of the polarization plane.There are two peaks in the y-axis,which indicates that the ionization probability is maximum when the electron emits out from the direction of y-axis.The blue solid line is accomplished through our simplified semi-classical model,which takes the Coulomb influence into account.Due to the effect of Coulomb potential,the angular distribution exhibits a clear asymmetry,and the two peaks are shifted to the second and fourth quadrants,respectively.The blue line is also consistent with the experimental results(denoted by the red dotted line),which proves that our model is correct and can be used to study the modulation of“Coulomb asymmetry”in an elliptically polarized laser field.

Fig.2 (Color online)Angular distribution of Ne in elliptically polarized laser field at an intensity of I=3.0×1014W/cm2.The ellipticity is χ =0.25.The wavelength is chosen as λ=795 nm in order to compare with the experiment.The green solid line is the case without Coulomb influence,the blue solid line is the result of our model and the red dotted line is obtained from experimental datas.[10]

In order to show the degree of asymmetry,we define the angle between the peak of the angular distribution and the minor polarization axis as the offset angle∆ϕ,as illustrated in Fig.2.Apparently,the bigger the offset angle is,the larger the peaks of angular distribution shift.We present in Fig.3 the influence of related atomic and laser parameters on the offset angle.From Figs.3(a),3(c),3(d),we can see that the offset angle decreases with the increasing of ionization potential,laser ellipticity and laser wavelength.They show a simply linear relation.However,the change of laser intensity has no effect on the offset angle.These phenomena can be explained as follows:the relationship between the emitting angle of the electron and the offset angle is∆ϕ =|π/2− ϕ|.According to our model,the emitting angle is

where pLyand pLxare respectively the y-momentum and x-momentum of electron caused by the laser field.Since the initial transverse velocity v⊥is Gaussian distribution(see Eq.(4)),the maximum ionization rate occurs when v⊥is equal to zero.In addition,the ionization is strongly dependent on field strength,thus the electron is most probably ionized at the peak of the field strength corresponding to the initial tunneling phase ωt0=0.Taking these conditions to Eq.(9),we obtain the expression of the offset angle analytically

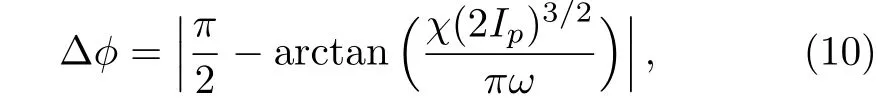
Equation(10)demonstrates that the offset angle varies inversely to ionization potential Ip,laser ellipticity χ and laser wavelength(λ =2πc/λ)but it is independent on the laser intensity,which is in accordance with the numerical simulated results.

In order to research the influence of atomic potential on the “Coulomb asymmetry” more deeply,we show the dependence of the emitting angle ϕ on the initial tunneling phase of the laser field and the initial transverse velocity of electron in Fig.4.Figure 4(a)is obtained with completely neglecting the Coulomb attraction.We can see that thisfigure presents an obvious symmetry.For example,region I and region II are symmetric about the line of ωt0=0 corresponding to the major axis of the polarization ellipse.The point(ωt0=0,v⊥=0.38)marked by a red circle is very special where produces an emitting angle of any value.The reason for this phenomenon is that when the initial tunneling phase is zero the tunneled electron has a laser-induced drift velocityin the y-direction.If the initial transverse velocity is equal but opposite to the drift velocity,i.e.vy0=−vd,they will counteract each other.This behavior leads the final momentum of electron to be zero.Under this situation,the emitting angle becomes arbitrary.When the ion-electron interaction is taking into account,the symmetrical structure of angular distribution is broken up,as seen in Fig.4(b).Figure 4(b)is a result of the combined laser and Coulomb field.The effect of Coulomb potential cannot be directly seen from it.To solve this problem,we use τ to denote the angle difference between the final momentum of electron in pure laser field and that in laser-Coulomb field.Then the deviations caused by Coulomb force between the two final momenta can be displayed by τ,see Fig.4(c).From this figure we can see that the Coulomb attraction mainly works in a narrow interval of phase near ωt0=0.Since the field strength is strongest at ωt0=0,the tunneling ionization rate reaches its maximum in this situation(see Fig.4(d),which is obtained from Eq.(3)),corresponding to the peaks of photoelectron angular distribution.This indicates that in the formation of“Coulomb asymmetry” the role of every electron is different.Only those electrons that tunnel out from the above narrow window of initial field phase are greatly effected by the Coulomb force and lead to the asymmetrical structure of electron angular distribution.

Fig.3 (Color online)The influence of ionization potential,laser intensity,laser ellipticity and laser wavelength on the offset angle.The parameters are:(a)χ=0.25,I=2.0×1014W/cm2,λ=795 nm;(b)χ=0.25,Ip=0.58 a.u.,λ=795 nm;(c)Ip=0.58 a.u.,I=2.0×1014W/cm2,λ=795 nm;(d)Ip=0.58 a.u.,χ=0.25,I=1.5×1014W/cm2,respectively.

Fig.4 (Color online)Dependence of the emitting angle ϕ on the initial phase of the laser field and the initial transverse velocity of the electron.(a)is the case in pure laser field.(b)is the result,which takes the Coulomb correction into account.(c)is the difference between(a)and(b),which is caused by the Coulomb potential.(d)exhibits the ionization rate as a function of the field strength.In this figure,the Xenon atom is subjected to elliptically polarized,χ=0.3,795 nm pulses at a peak intensity of 2.0×1014W/cm2.

4 Summary

In this paper,we bring a semiclassical tunneling model and a Coulomb correction from Ref.[9]together to study the modulation of“Coulomb asymmetry” in an elliptically polarized laser field.The simulated result is in good agreement with the experiment.The degree of“Coulomb asymmetry”can be represented by offset angle,which is easily effected by ionization potential,laser ellipticity and laser wavelength:the offset angle decreases with the three parameters increase.So the above three parameters can be used to adjust the asymmetric degree of angular distribution.However,the offset angle has nothing to do with laser intensity.We have derived an analytical formula to account for these phenomena.In addition,through comparing the difference of emitting angle obtained respectively in pure laser field and combined Coulomb-laserfield,the contribution of Coulomb potential on the asymmetrical structure can be directly observed.It shows that the Coulomb influence mainly functions on those electrons that tunneled out from a certain window of initial field phase(adjacent to ωt0=0).Our computing method is simple and efficient,and the results have a reference meaning for using the attoclock technique to characterize the quantum tunneling process.