Practical Reference-Frame-Independent Measurement-Device-Independent Quantum Key Distribution Systems Against the Worst Relative Rotation of Reference Frames∗

Chun-Mei Zhang(张春梅),Jian-Rong Zhu(朱建荣),and Qin Wang(王琴)

Institute of Quantum Information and Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Key Laboratory of Broadband Wireless Communication and Sensor Network Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

AbstractReference-frame-independent measurement-device-independent QKD(RFI-MDI-QKD),immune to both the slow unknown drift of reference frames and detector side channel attacks,can generate information-theoretic secure keys.Despite its natural resistance to the slow drift of reference frames,the performance of practical RFI-MDI-QKD systems descends with the increasing drift of reference frames.In this paper,we demonstrate the worst relative rotation of reference frames for practical RFI-MDI-QKD systems,and investigate their performance against the worst-case scenario,both of which are unclear to date.Simulation results show that,practical RFI-MDI-QKD systems can achieve quite good performance even against the worst-case scenario,which clearly demonstrates that it is possible to implement practical MDI-QKD systems with freely drifting reference frames.

Key words:reference-frame-independent,measurement-device-independent,quantum key distribution,relative rotation

1 Introduction

Based on the laws of quantum physics,quantum key distribution(QKD)[1]provides a method to generate information-theoretic secure keys between two remote peers Alice and Bob,even in the existence of an eavesdropper Eve. Nevertheless,imperfect devices adopted in practical QKD systems compromise its theoretical security.[2−6]To defeat attacks aimed at the measurement device,which is the most fragile part in real-life QKD systems,measurement-device-independent QKD(MDI-QKD)[7−8]was proposed,and has been widely studied.[9−20]In practical QKD systems,shared reference frames are very crucial,without which they will suffer from severely high quantum bit error rates(QBERs).Generally,the reference frames between Alice and Bob should be carefully aligned to make QKD systems running normally,[14−21]which however,is usually timeconsuming,complicated,and will reduce the secret key rate.

To avoid the alignment of reference frames,Laing et al.proposed reference-frame-independent QKD(RFIQKD),[22]which can generate secret keys even with the slow drift of reference frames,and related works on RFIQKD have been reported.[23−31]Unfortunately,RFI-QKD still suffers from the detector side channel attacks.To overcome this problem,Yin et al.proposed RFI MDIQKD(RFI-MDI-QKD),[32]which is inherently immune to both the slow drift of reference frames and detector side channel attacks.

In RFI-MDI-QKD,Alice(Bob)encodes quantum states in three orthogonal bases Z,X,and Y,whereDenote her(his)local bases as ZA(B),XA(B),and YA(B),respectively.The Z basis between Alice and Bob aligns well for usual encoding schemes,while the X and Y bases drift slowly with the unknown angle βA(B).In other words,

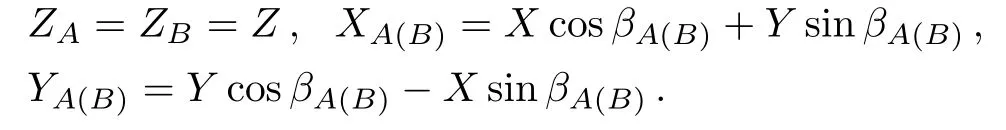
They distill secure keys from data in Z basis,and estimate the amount of Eve’s information from data in X and Y bases.

Recently,RFI-MDI-QKD has drawn a lot of attention both in theories and experiments.[33−37]However,despite its robustness against the slow drift of reference frames,the performance of practical RFI-MDI-QKD systems declines with the increasing drift of reference frames.Hence,it is natural to ask what the worst relative rotation of reference frames for practical RFI-MDI-QKD systems is,and how well they can perform against the worst-case scenario.In this paper,we demonstrate the worst relative rotation of reference frames for practical RFI-MDI-QKD systems mathematically,and investigate their performance against the worst-case scenario.Simulation results show that,practical RFI-MDI-QKD systems can achieve quite good performance even against the worst relative rotation of reference frames,which demonstrates the feasibility of MDI-QKD systems with freely drifting reference frames.

2 The Worst Relative Rotation of Reference Frames for Practical RFI-MDI-QKD Systems

To make the demonstration more practical and universal,the decoy-state method[38−39]is adopted in practical RFI-MDI-QKD systems with the most widely used weak coherent sources. For simplicity and without loss of generality,we consider the three-intensity(signal+decoy+vacuum)[40]decoy-state RFI-MDI-QKD scheme with infinite number of pulses temporarily,where Alice(Bob)randomly prepares signal states of intensityµwith bases ZA(B),XA(B),and YA(B),decoy states of intensity ν with bases ZA(B),XA(B),and YA(B),and vacuum states of intensity ω with no basis.With measurement results announced by the third party Charles,Alice and Bob can get a series of gains and QBERs of different intensity and basis combinations,denoted asand,respectively,where λA(B)∈ {µ,ν,ω},and∈ {ZA(B),XZ(B),YA(B)}.In this scheme,the valid basis combination ζAζBsatisfies∈ {ZAZB,XAXB,XAYB,YAXB,YAYB}.We emphasize that,in spite of the state preparation rules mentioned earlier,it is beneficial to regard vacuum states of intensity ω as states prepared with basis ZA(B),XA(B),or YA(B)occasionally.

The gain of quantum states of intensities λAand λBwith basis combination,is given as

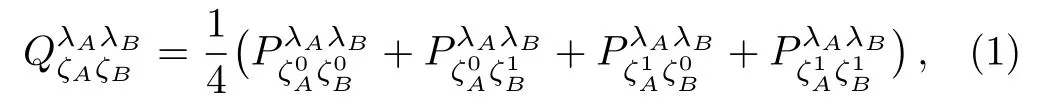
The QBER of quantum states of intensities λAand λBwith basis combination,,is given as

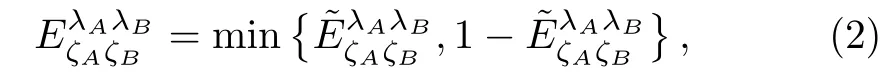
With Eqs.(1)and(2),Alice and Bob can estimate the lower bound of single-photon yield and the upper bound of single-photon error rate,denoted asand,respectively.[43]

Then,the secret key rate they can distill in decoy-state RFI-MDI-QKD[32]is

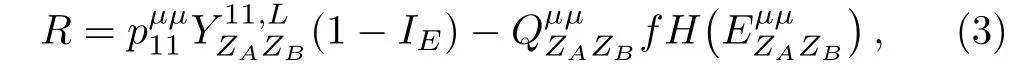
More specifically,Eve’s information IEis given as

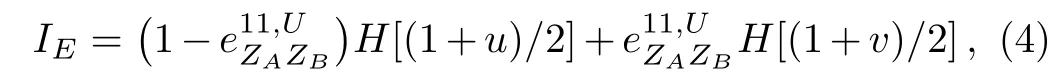
where

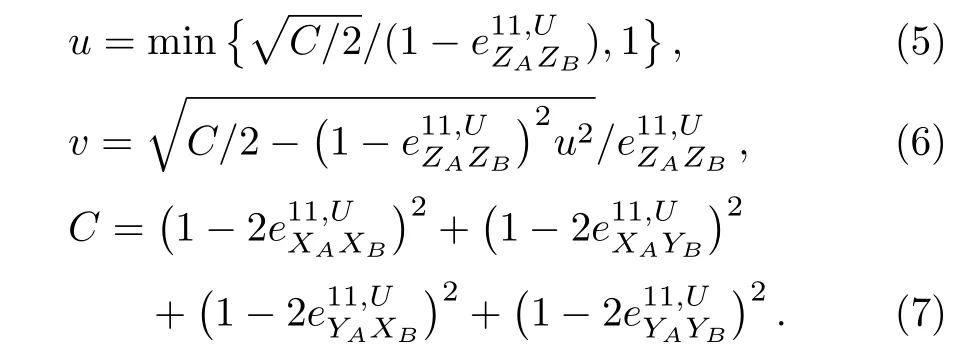
Due to the nature of RFI-MDI-QKD mentioned in Sec.1,we know that the relative rotation of reference frames between Alice and Bob,defined as∆β=βB−βA,only influences data collected in XAXB,XAYB,YAXB,and YAYB.As shown in Eqs.(3)and(4),∆β only infl uences Eve’s information IE.In more detail, ∆β only affects the value of C.Hence,the demonstration of the worst∆β for practical RFI-MDI-QKD systems switches to the demonstration of the worst∆β for C.

To clearly demonstrate the performance of C against different∆β,we empirically setµ∈{0.50,0.55,0.60,0.65}and ν=0.01 at 100 km of the standard fiber link,which will definitely not alter the behavior of C against∆β.Other related system parameters are given in Sec.3.First,by some mathematical calculations,we can prove that C is a periodic function of∆β,and the minimal positive period of C is π/2.That is,C(∆β)=C(∆β +nπ/2),where n=±1,±2,...Then,we can further prove that the symmetry axis of C is π/4 in the domain[0,π/2],which means C(π/4+ ∆β)=C(π/4− ∆β).Figure 1 shows the corresponding performance of C against different∆β in two periods with infinite number of pulses.As illustrated in Fig.1,the minimal positive period of C is π/2,and the performance of C reaches its worst at the symmetry axis,where ∆β is π/4 or 3π/4.Moreover,we can see that the value of C declines with the increase ofµ.Correspondingly,to calculate the worst∆β in mathematical form,we calculate the derivative of C in the domain(0,π/2),denoted as

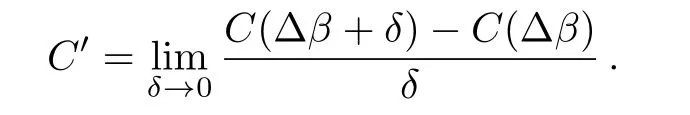
We find C′(π/4)=0,C′(∆β1)<0,and C′(∆β2)>0,where 0< ∆β1< π/4,and π/4< ∆β2< π/2,and the results are shown in Fig.2.Considering the periodicity of C,we demonstrate that the worst relative rotation of reference frames∆β for C is∆β=mπ/4,where m is an odd number.Hence,the worst relative rotation of reference frames∆β for practical RFI-MDI-QKD systems is∆β =mπ/4,where m is odd.Note that,the inflection points in Fig.2 originate from Eq.(2),where either Alice or Bob performs bit flips on her or his bit strings to make≤ 0.5.

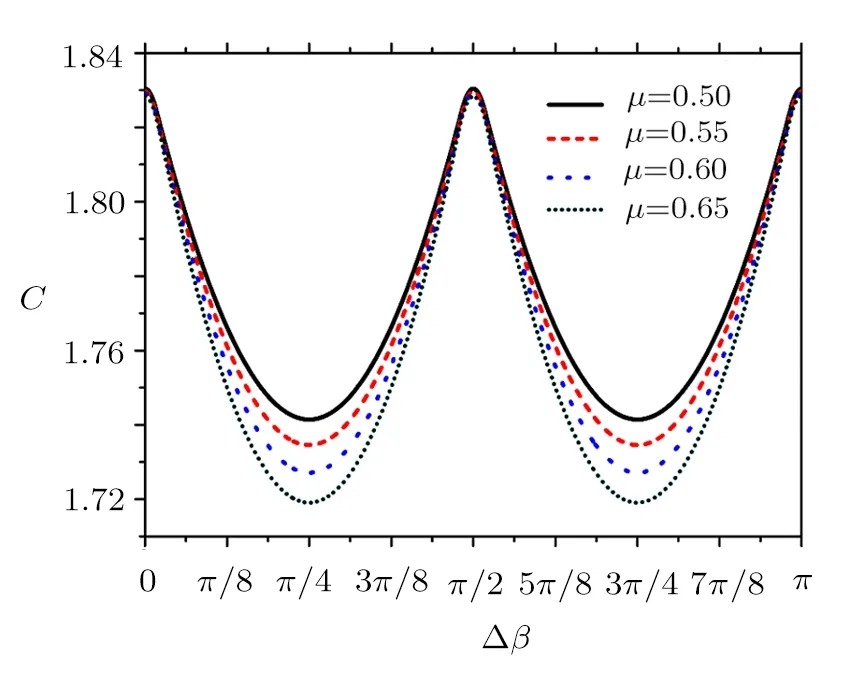
Fig.1 (Color online)Performance of C against different relative rotations of reference frames∆β in two periods with infinite number of pulses.

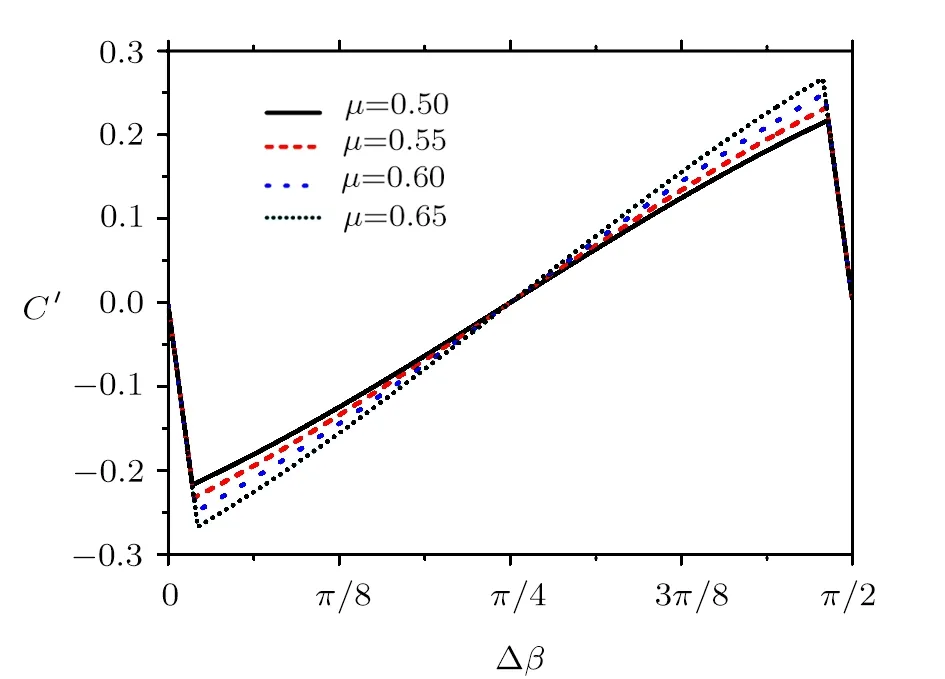
Fig.2(Color online)Performance of C′against different relative rotations of reference frames∆β in the domain(0,π/2)with infinite number of pulses.

With the help of the Bloch sphere,the physics behind this demonstration in practical RFI-MDI-QKD systems can be well explained:(i) ∆β =0 means Alice’s XAand YAbases are perfectly aligned with Bob’s XBand YBbases,which is certainly the ideal case and will lead to the best performance;(ii) ∆β = π/2 means Alice’s XAbasis is aligned with Bob’s YBbasis and Alice’s YAbasis is aligned with Bob’s XBbasis,which is essentially the ideal case due to the high symmetry of C and will lead to the best performance again;(iii)∆β= π/4 means Alice’s XAand YAbases are aligned with Bob’s XBand YBbases in the most chaotic way,which will lead to the worst performance.

3 Simulation

Assume the dark count rate per pulse and detection efficiency of single-photon detectors are 3 × 10−6and 14.5%,the loss coefficient of the standard fiber link is 0.2 dB/km,the optical intrinsic error rate is 1.5%,and the inefficiency of the error correction procedure is 1.16.For simplicity and without any compromise of security,only the B√ell state measurement results projected intoare considered.

By the fullparameter optimization method,[43]weinvestigatetheperformanceofpracticaldecoystate RFI-MDI-QKD systems in[0,π/2]for statisticalfluctuations[41]when the total number of photon pulses is N=1012.According to Ref.[41],the upper(lower)bounds ofand,denoted asand,U(L),can be given as

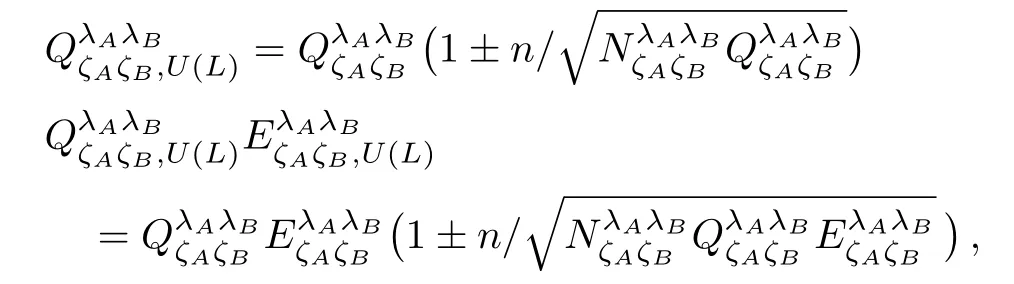
respectively,where n denotes the number of standard deviations,anddenotes the number of pulses of intensities λAand λBwith basis combination.In our simulation,we set n=5.We emphasize that,due to the periodicity of Eq.(3),it is sufficient to study the performance of RFI-MDI-QKD in the domain[0,π/2].Figure 3 shows the secret key rates of RFI-MDI-QKD with∆β =0,π/8,π/4,3π/8,π/2,where the solid lines from right to left denote results of ∆β =0,π/8,π/4,respectively,and the dotted lines from right to left denote results of∆β = π/2,3π/8,respectively.As illustrated in Fig.3,the performance of practical RFI-MDI-QKD systems is obviously the worst when∆β=π/4,and the overlapped lines of∆β =0,π/2 and ∆β = π/8,3π/8 show the symmetry of Eqs.(3)and(7).Furthermore,even against the worst∆β= π/4,RFI-MDI-QKD can still achieve a distance of more than 60 km,which is quite robust in practical QKD systems.Correspondingly,we give the optimal intensities of signal and decoy states in Fig.4.Notice that,to show the performance of practical RFI-MDI-QKD systems against the worst-case scenario more clearly,results in Figs.3 and 4 are simulated with the traditional method(see the next paragraph for details).

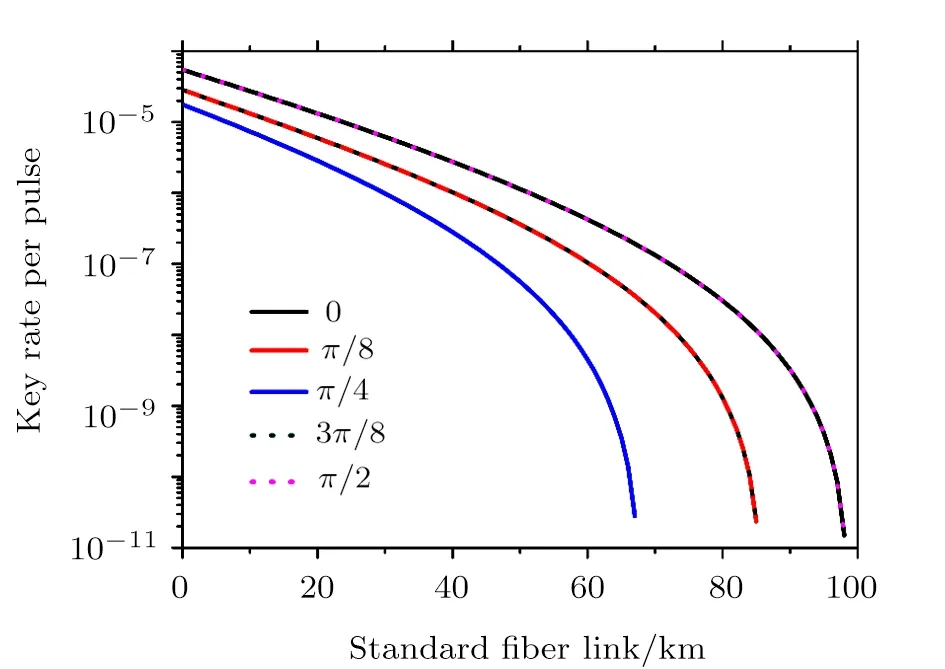
Fig.3(Color online)Secret key rates per pulse of decoystate RFI-MDI-QKD against different relative rotations of reference frames∆β with N=1012with full optimized parameters.The solid lines from right to left denote results of∆β =0,π/8,π/4,respectively,and the dotted lines from right to left denote results of∆β = π/2,3π/8,respectively.

Fig.4 (Color online)Optimal intensities of decoy-state RFI-MDI-QKD against different relative rotations of reference frames∆β with N=1012with full optimized parameters.The six solid lines from top to bottom denote the signal intensities of∆β =0,π/8,π/4 and the decoy intensities of∆β =0,π/8,π/4,respectively,and the four dotted lines from top to bottom denote the signal intensities of∆β = π/2,3π/8 and the decoy intensities of∆β = π/2,3π/8,respectively.

In some cases,Alice and Bob can get a relatively good estimation of∆β,and then they can use the estimated∆β to investigate the performance of practical RFI-MDIQKD systems during a short period of time,which is denoted as the traditional method.It should be noted that,the essence of RFI-MDI-QKD is providing a feasibility to distribute secret keys when the reference frames suffer from the unknown drift.This means Alice and Bob cannot always get a good estimation of∆β.Hence,it is advisable to investigate the performance of practical RFIMDI-QKD systems against the worst-case scenario.In practical RFI-MDI-QKD systems with unknown relative rotation of reference frames,Alice and Bob optimize all related parameters with the worst∆β = π/4,which is denoted as the new method.

By optimizing all system parameters(including intensities of signal and decoy states and corresponding bases choices),we study the performance of the two methods in the domain[0,π/2]at 50 km of the standard fiber link with N=1012.Corresponding results are shown in Fig.5.The red triangles denote results of the new method,and the blue squares denote results of the traditional method.As shown in Fig.5,different from the traditional method,the new method does not require a good estimation of∆β,which is more reasonable and universal than the traditional method,and adheres to the essence of RFI-MDIQKD strictly.

Fig.5 (Color online)Comparison of the new and traditional methods in decoy-state RFI-MDI-QKD against different∆β in the domain[0,π/2]at 50 km with N=1012.The red triangles denote results of the new method,and the blue squares denote results of the traditional method.

4 Conclusion

In conclusion,we have demonstrated the worst relative rotation of reference frames for practical RFI-MDIQKD systems,which is vital for thorough investigations in RFI-MDI-QKD.With the worst-case scenario,we study the performance of practical RFI-MDI-QKD systems with full optimized system parameters. Our simulation results show that practical RFI-MDI-QKD systems can obtain very good performance even against the worst relative rotation of reference frames,which exhibits signi ficant robustness and demonstrates the possibility of practical MDI-QKD systems with slowly free drifting reference frames.Moreover,we propose a new method to investigate the performance of practical RFI-MDI-QKD systems,which is more universal than the traditional method and adheres to the essence of RFI-MDI-QKD rigorously.It should be pointed out that,in terms of the imperfect encoding devices in MDI-QKD systems,the security of RFIMDI-QKD[37]can still be guaranteed with the method in Refs.[9–10,20].