海因里希事故金字塔模型探究

郑社教

(中国石油天然气集团有限公司长庆油田分公司培训中心，陕西 西安 710021)

1 海因里希事故金字塔模型及其意义

1941年，美国的安全工程师海因里希统计了55万件机械事故，其中死亡、重伤事故1 666件，轻伤48 334件，其余则为无伤害事故。经过数据分析后，得出一个重要结论：即在机械事故中，死亡、重伤与轻伤和无伤害事故的比例为1∶29∶300，国际上把这一法则叫事故法则。这个法则说明，在生产过程中，每发生330起机械事故，就有300起未产生人员伤害、29起造成人员轻伤和1起导致重伤、死亡。海因里希事故金字塔模型如图1所示。

图1 海因里希事故金字塔模型

后来，人们结合海因里希的事故因果连锁理论，即事故发生的直接原因是人的不安全行为和物的不安全状态，并将二者合并为不安全因素(也可以称为危害因素)，将海因里希事故金字塔模型发展成图2所示的金字塔模型。

根据海因里希事故金字塔模型可知几点结论。

(1) 在当时条件下，某行(企)业如发生330起机械事故，其死亡或重伤、轻伤、未遂事件的比例为1∶29∶300。但该数值不适应于其他行业或其他事故。

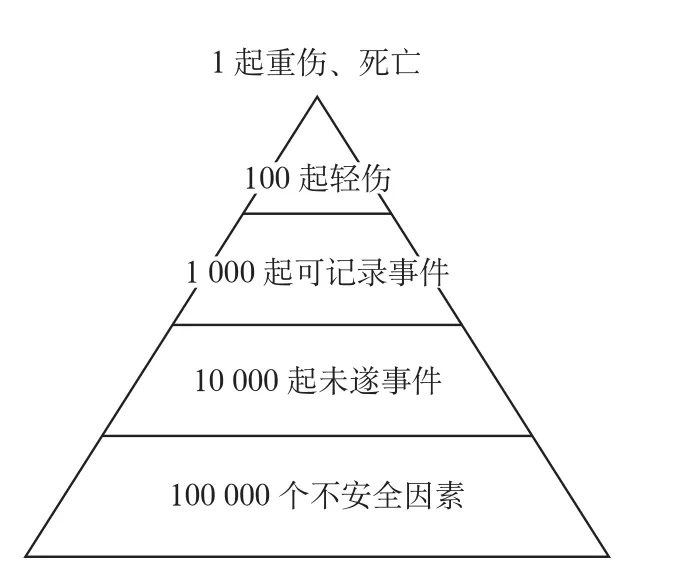
图2 海因里希事故金字塔模型的发展

(2) 虽然一次不安全因素的后果是偶然的，可能是未遂事件、轻伤或重伤，无法判定，但大量的不安全因素导致的后果是必然的。即大量的不安全因素，必然引起一定次数的未遂事件，较少次数的轻伤和不可接受的伤害(重伤或死亡)。在一定的安全管理与技术条件下，对不同行业、不同企业、不同事故各有一定的比例。

(3) 安全管理的实质就是要预防不安全因素；只有消除了不安全因素，才能预防事故。

海因里希事故金字塔模型出现后，在安全管理领域得到了普遍应用，人们试图用该金字塔模型指导安全管理；也使人们的安全观念发生了质的变化。但人们对该金字塔模型的认识也存在一些误区。

2 海因里希事故金字塔模型的认识误区

经过考察有关企业安全管理状况，结合有关安全管理人员在工作中的表现，发现人们对海因里希事故金字塔模型的认识有如下误区。

(1) 忽视了海因里希事故金字塔模型的产生背景，将金字塔模型的1∶29∶300的数值推广到所有行(企)业的所有事故类型。具体表现在，一些管理人员错误的认为1∶29∶300是通用的，试图利用该数据来解释本单位的安全问题，甚至试图将本企业的统计数据回归到1∶29∶300上。但海因里希事故金字塔模型是在当时条件下统计某行(企)业机械事故时得出的，1∶29∶300的数值仅仅适应于当时情况。

(2) 忽视了海因里希事故金字塔模型是动态变化的。海因里希事故金字塔模型是在一定的管理和技术条件下得出的，当企业管理和技术条件变化时，统计数值将会发生变化，因此模型是动态变化的。管理人员不能不顾管理与技术条件的变化，而墨守1∶29∶300 的数值。

(3) 对海因里希事故金字塔模型形状的变化含义缺乏认识，影响了该模型在安全管理中指导作用的发挥。应当说金字塔模型的形状是变化的，不同形状反映了各个行(企)业在不同条件下的危险性以及安全管理状况。

(4) 对事故金字塔的绘制方法尚无统一规定，影响了该模型的规范使用。

3 海因里希事故金字塔模型的绘制

要深入应用海因里希事故金字塔模型，首先必须规范绘制方法。关于该事故金字塔模型的绘制方法，目前尚无标准。

3.1 海因里希事故金字塔模型的假定

海因里希事故金字塔模型的形状，与不可接受的伤害事件起数、轻伤事件起数、未遂事件起数与不安全因素个数之间的关系有关。这个关系可分为2种，即线性关系和非线性关系。对于简单事故，假定不可接受的伤害事件起数、轻伤事件起数、未遂事件起数与不安全因素数量之间呈线性关系，那么金字塔模型应该是等腰三角形；对于复杂事故，影响因素和控制规律比较复杂，不可接受的伤害事件起数、轻伤事件起数、未遂事件起数与不安全因素数量不成线性关系，那么金字塔模型就不是等腰三角形，而应该是等腰曲边三角形或等高阶梯矩形，如图3、图4 所示。

图3 事故金字塔理想模型(线性关系)

图4 事故金字塔模型(非线性关系)

3.2 海因里希事故金字塔模型的绘制方法

要正确绘制海因里希事故金字塔模型，应该采取如下步骤。

(1) 客观统计企业在一定时间段的安全事故。最好按照不同事故类别来统计，当然也可以按照总事故数来统计。应统计重伤或死亡起数、轻伤起数、未遂事件起数和不安全因素(不安全行为、不安全状态)个数。如果按照不同事故类别(如高处坠落、机械伤害、物体打击等等)来统计，那么重伤或死亡起数、轻伤起数、未遂事件起数和不安全因素(不安全行为、不安全状态)个数都应当是某类事故的数据。统计数据可以来自事故、事件台账，行为安全观察的结果或其他统计方法。

(2) 对原始数据进行整理。应剔除不可靠的数据和无效数据，然后对原始数据进行约分处理，使重伤、死亡起数为1，从而得出相应的轻伤起数、未遂事件起数和不安全因素个数。

(3) 绘制海因里希事故金字塔。

① 绘制时最好在标准的坐标纸上绘制，首先应规定各个“梯级”(即横线之间的间距)的高度，并保证高度相等，以方便进行比较。

② 建立坐标系。以不安全因素个数线段所在直线为横轴，以不安全因素线段左端点(也可以是中点)为原点，建立坐标系。然后用线段或矩形的长度表示相应起数，计算相应的坐标值，得出相应起数的坐标点。

③ 尽量用直线连接各个坐标点，如果不能则用平滑的曲线连接各个坐标点，形成海因里希事故金字塔，如图5所示。

绘制时应注意其对称性。为了方便处理，也可采用等高阶梯矩形的形式来绘制。

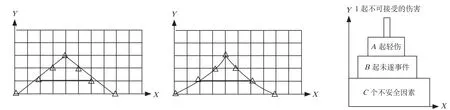
图5 金字塔模型的绘制

3.3 海因里希事故金字塔模型的其他绘制方法

海因里希事故金字塔都是以不安全因素个数为基本变量绘制的。在实际应用中，由于不安全因素数量难以准确获得，可以采取其他基本变量。常以项目建设投资、企业产值、运行工时等进行统计等，如图6—8所示。

4 金字塔模型的安全指导意义

有了标准的海因里希事故金字塔模型，就可以对其进行比较。比较时应采用同类模型(同事故类别、同种金字塔)。

4.1 安全管理的重点

海因里希事故金字塔模型的一个重要结论就是安全管理的重点要由传统的对事故的管理转向对不安全因素(危害因素)的管理，从治标转向治本，要尽量减少或消除不安全因素，以预防事故。

4.2 不同类型事故的比例关系

不同行业，甚至同行业不同企业的不同类型事故，该比例是不同的，不一定是1∶29∶300，也一定不是 1∶100∶1 000∶10 000∶100 000。具体比例数值与企业的固有危险性、安全管理状况、技术条件和事故机理等因素有关。各企业应统计各自的事故数据，寻找各自的比例关系。该比例关系反映了企业当时安全管理和技术条件下的关系，能够代表企业某类事故的发生规律，具有一定的指导意义。

4.3 海因里希事故金字塔的变化

按照以上画法画出的海因里希事故金字塔，其形状反映了该企业某种事故的危险性。金字塔底边越宽（越扁平），反映了危害因素引发事故难度越大，亦即较多的不安全因素才会引发一起不可接受的伤害事件；反之金字塔越尖锐，说明较少的不安全因素就会引发一起不可接受的伤害事件。因此，安全管理的目的是尽量减少不安全因素，避免不可接受的伤害事件发生，使统计出的海因里希事故金字塔模型越来越扁平。

4.4 海因里希事故金字塔模型的极端图形

作为上一条的补充，海因里希事故金字塔模型有2个极端图形，即极端危险环境的金字塔和绝对安全环境的金字塔。前者情况是，只要出现一个不安全因素，就会导致1起死亡或重伤。这种情况下，事故金字塔变成了一条竖直线段，如图9(a)所示。与之相反的绝对安全环境(理论上不存在)，就是引发一起不可接受的伤害事件，需要无限个不安全因素。这时事故金字塔底边变得无限长，等腰三角形顶点无限接近底边，事故金字塔变成了一条无限长的横直线，如图9(b)所示。

图6 以工程投资表示的金字塔模型

图7 以企业产值表示的金字塔模型

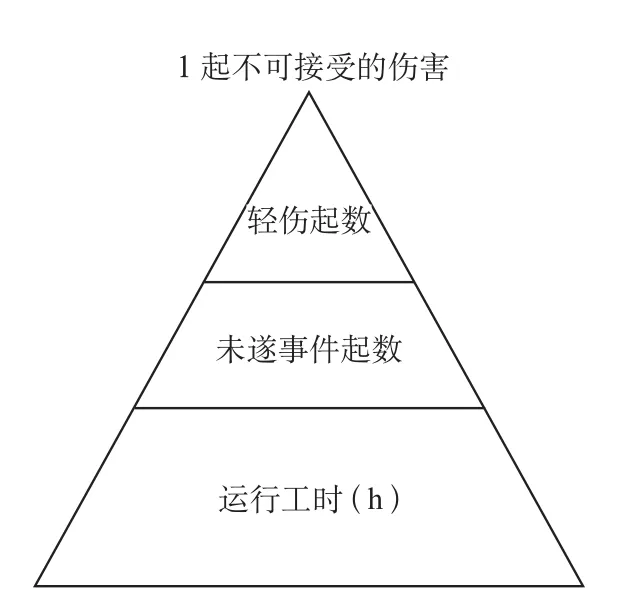
图8 以运行工时表示的金字塔模型

5 结束语

海因里希事故金字塔模型自提出以来，在安全管理中发挥着重要的指导意义，应从以下几个方面来理解。

(1) 海因里希事故金字塔模型是通过对大量数据的统计得出的。各个企业各自统计得出的事故金字塔可以作为安全管理和安全系统预测的依据。

(2) 事故金字塔模型是建立在科学管理的基础之上的。一个行业、企业或单位，应自觉采用科学的管理方法，持续对有关安全数据进行统计、分析，并考察事故金字塔形状的变化，这是提高安全管理水平的有效手段。对安全数据进行持续统计分析使其成为安全决策的依据。

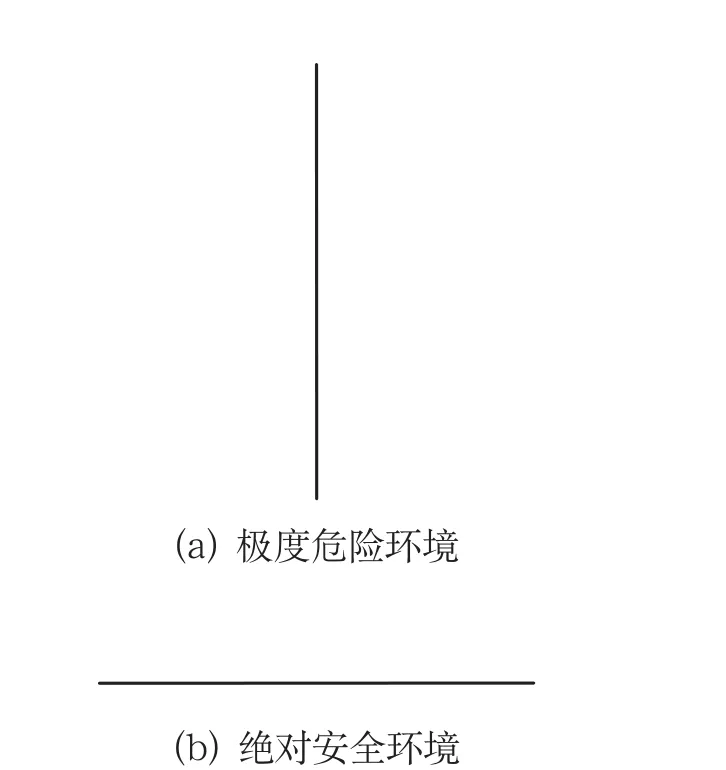
图9 极端环境的海因里希事故金字塔模型

（3） 针对目前普遍采用的行为安全观察与沟通这一安全管理方法，应建立一套科学的观察数据整理、统计和分析方法，把安全观察数据与事故金字塔模型结合起来，充分发挥这一方法的作用。

(4) 不安全因素统计难度很大，也需要一定的方法与技术，但未遂事件、轻伤、重伤和死亡数据统计则比较容易。因此，建议企业采取适合各自情况的海因里希事故金字塔模型，如以企业产值、运行工时为基本变量的金字塔模型，以期达到事半功倍的效果。