基于三次指数平滑法的铁路旅客发送量预测研究

曹志成，刘伊生，董继伟

（北京交通大学经济管理学院，北京100044）

0 引言

随着我国高速铁路建设的不断发展，高速铁路以其载客数量大、耗时少、安全性强、正点率高等特点吸引着越来越多的旅客作为其出行的首选交通方式。据统计，2008—2017年我国铁路旅客发送量年均增长8.70%，铁路旅客发送量呈现逐年增长的态势。只有铁路的运输能力匹配客运需求，才能确保铁路营运畅通，提高运输质量[1]。因此，科学有效地预测铁路旅客发送量，有利于铁路资源合理配置，促进我国铁路运输健康发展[2]。

目前，铁路旅客发送量预测的研究方法主要采用线性回归分析、灰色预测法、马尔科夫预测模型、神经网络模型等。例如，陈鹏等[3]采用灰色GM (1，1)模型和马尔科夫模型相结合形成的一种新的灰色马尔科夫铁路客运量预测模型对铁路客运量进行预测；郝军章等[2]建立SARIMA模型，并经过逐期差分和季节差分后最终建立ARIMA (1，2，2)×(1，1，1)6模型，并对我国铁路客运量进行预测；侯丽敏等[4]运用灰色预测理论构建灰色模型GM (1，1)与线性回归相结合的数学模型，并对河南省的铁路客运量进行了预测；杨祺煊[5]针对铁路客运量变量关系复杂、影响因素多的特点，建立了主成分分析与GA-BP网络相结合的预测模型，并对天津铁路客运量进行了预测；王枭[6]提出了一种优化的遗传算法模型，并对我国铁路旅客发送量进行了预测。上述方法虽然对我国铁路旅客发送量进行了较好预测，但存在可信度低、周期长[7]等缺点。三次指数平滑法能够根据时序的变化，清晰地显示出时序的变化趋势，对波动范围较大且呈非线性变化规律的数据具有很强的适用性，具有预测可信度较高、基础数据周期要求短、操作便捷且使用方便等优点，而铁路旅客发送量数据具有一定的波动性，并呈现出一定的非线性变化趋势。因此，选用三次指数平滑法对铁路旅客发送量进行预测，并通过实例验证其适用性。

1 基于三次指数平滑法的铁路旅客发送量预测模型

指数平滑法是一种时间序列分析预测法，该方法是通过计算指数的平滑值，结合合理的时间序列预测模型，根据目前的现状数据对未来趋势进行预测。三次指数平滑法是指数平滑法的一种，适用于时间序列呈现抛物线趋势的非线性数据，使用便捷，在各个领域均有应用[8]。

1.1 构建基于三次指数平滑法的铁路旅客发送量预测模型

以n年为原始时间序列的期数，即选取铁路旅客发送量数据的期数。记Xt为第t年的铁路旅客实际发送量(t= 1，2，…，n)，预测未来年的铁路旅客发送量。

构建基于三次指数平滑法的铁路旅客发送量预测模型为

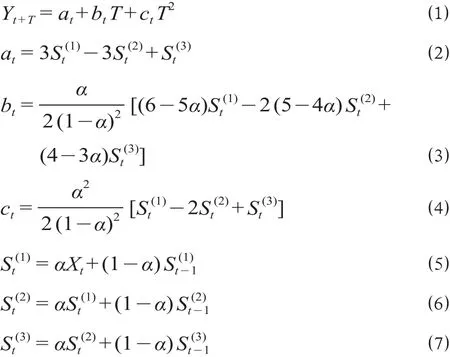
式中：Yt+T为当期铁路旅客发送量预测值；T为预测超前期数；at，bt，ct为第t年的预测系数；分别为第t年对应的一次、二次、三次指数平滑值；α为权重系数，且分别为一次、二次、三次指数平滑的平滑初始值。

1.2 模型求解

（1）确定初始值。在一般的指数平滑法预测过程中，当原始时间序列的期数较多(一般为大于15项)时，可认为初始值对预测结果产生的影响较小，因而选择原始数列第1期的实际数据值作为初始值；当原始时间序列的期数较少(一般为小于15项)时，可认为初始值对预测结果产生的影响较大，因而一般选择原始数据前3期的平均值作为初始值。

（2）选择权重系数。权重系数α是在预测过程中，新旧数据起不同作用的比例因子[9]，0 ＜α＜ 1。α越大，表明预测中对新数据重视度越高，新数据所起作用越大，预测结果的灵敏度越高，适应新水平能力越好；α越小，表明预测中对旧数据的重视程度越高，预测结果比较保守，对实际数据的变动反应较迟缓，易于产生滞后性。通常情况下，α取值的规律为：当时间序列呈现较稳定的水平趋势时，选取较小的α值，一般在0.05 ～ 0.2之间取值；当时间序列有波动，但长期趋势变化不大时，选取稍大的α值，一般在0.3 ～ 0.5之间取值；当时间序列波动很大，长期趋势变化幅度较大，呈现明显且迅速的上升或下降趋势时，选取较大的α值，一般在0.6 ～ 0.8之间取值。

（3）进行数据预测。①将求得的初始值与权重系数α代入公式 ⑸ 至公式 ⑺，得出一次、二次、三次平滑修匀新数列值；②根据公式 ⑵ 至公式 ⑷计算各年的预测系数，为三次指数平滑计算提供基础；③根据三次指数平滑公式 ⑴，选取合适的预测超前指数，对未来数据进行预测，并得到最终的结果。

2 实例分析

以我国铁路旅客发送量的预测为例，选取2008—2017年我国铁路旅客发送量数据作为原始数据样本，预测2018年、2019年我国铁路旅客发送量数据。

2.1 选取基础数据

2008—2017年我国铁路旅客发送量如表1所示。

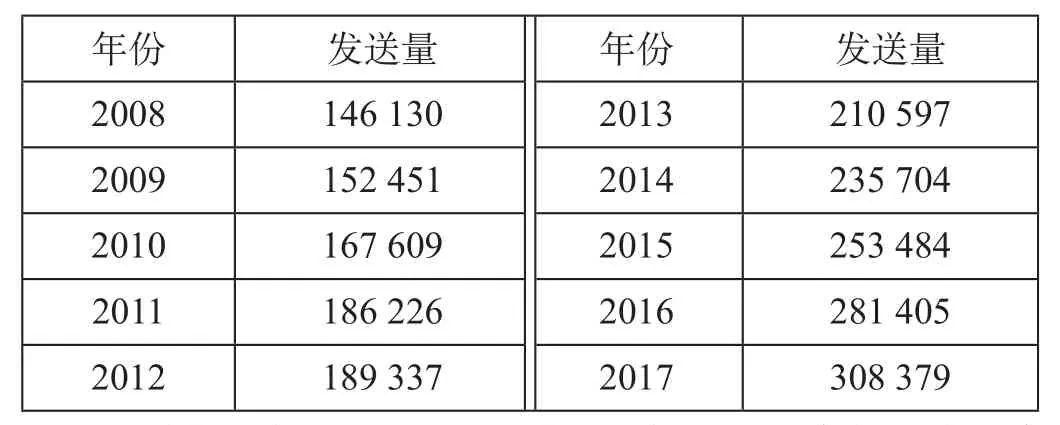
表1 2008—2017年我国铁路旅客发送量 万人Tab.1 National railway passenger volume from 2008 to 2017

2.2 确定初始值

根据表1中2008—2017年我国铁路旅客发送量数据可看出原始时间序列的期数n= 10，小于15，因而选择原始数据的前3者取平均值作为平滑初始值，可得

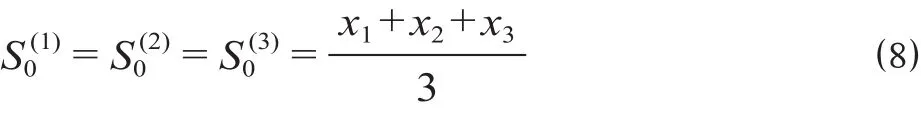
将表1中的原始数据代入公式⑻可得

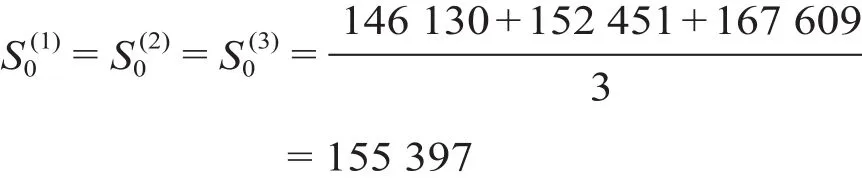
2.3 确定权重系数

为了观测2008—2017年我国铁路旅客发送量的变化情况，计算出每年铁路旅客量的变化值，即相邻2年旅客量的差值。通过计算得到2008—2017年我国铁路旅客发送量变化值如表2所示。

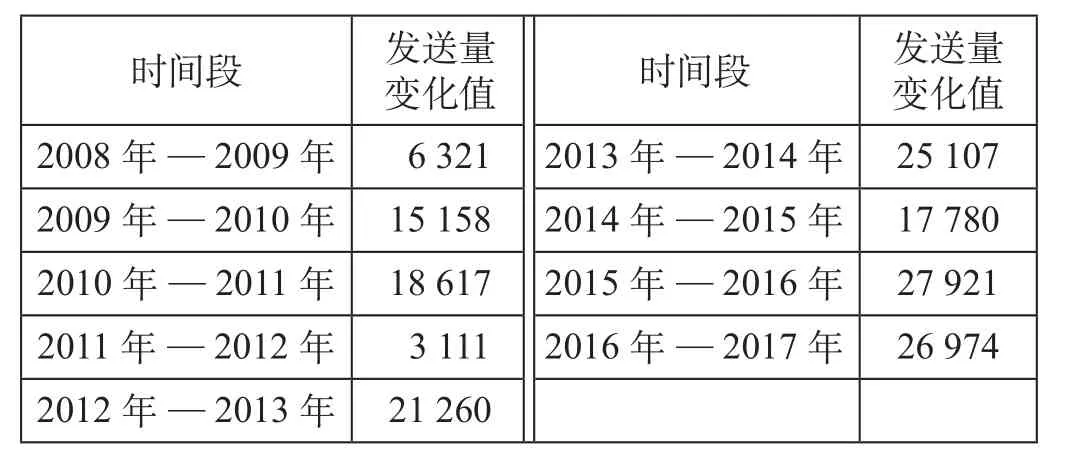
表2 2008—2017年我国铁路旅客发送量变化值 万人Tab.2 Variation value of railway passenger transport in China from 2008 to 2017

可以看出，我国铁路旅客发送量存在波动，除2008—2009年和2011—2012年2个时间段的波动较大以外，其他时间段的斜率值基本稳定在2 000左右，因而长期趋势变化不大，α可在0.3～0.5之间取值。在实际的权重系数确定过程中，通常情况下会在取值范围内选择几个α进行试算，之后根据实际数据与预测结果比较后，选择误差较小者。为了选择准确的α值，分别选取α= 0.3，α=0.4，α= 0.5对我国铁路旅客发送量进行预测，α=0.3，α= 0.4，α= 0.5时预测值与实际值对比结果如表3所示。

由表3可以看出α= 0.5时，预测值与实际值的误差较小，且2016、2017年的预测值基本上与实际值相差无几，预测误差分别为0.86%、0.42%。因此，选用α= 0.5作为预测权重系数。

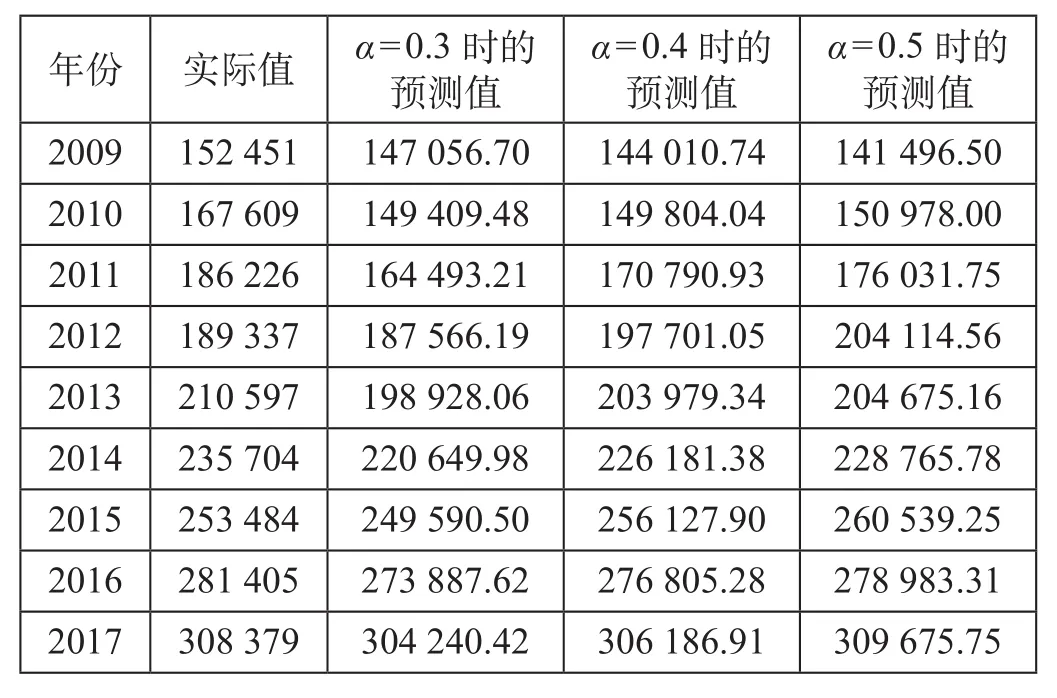
表3 α = 0.3，α = 0.4，α = 0.5时预测值与实际值对比结果万人Tab.3 Comparison between predicted value and actual value at α = 0.3, α = 0.4, α = 0.5

2.4 模型预测

2.5 预测结果分析

（1）预测结果与实际数据比较分析。为了分析实际数据与预测结果之间是否具有较高的相关性，对2009—2017年的实际数据与预测结果采用皮尔逊相关系数进行检验，皮尔逊相关系数是一种度量2组数据相关程度的方法。运用SPSS对数据进行分析处理后得到α= 0.05时实际值与预测值相关性的计算表。实际值与预测值相关性计算表如表5所示。

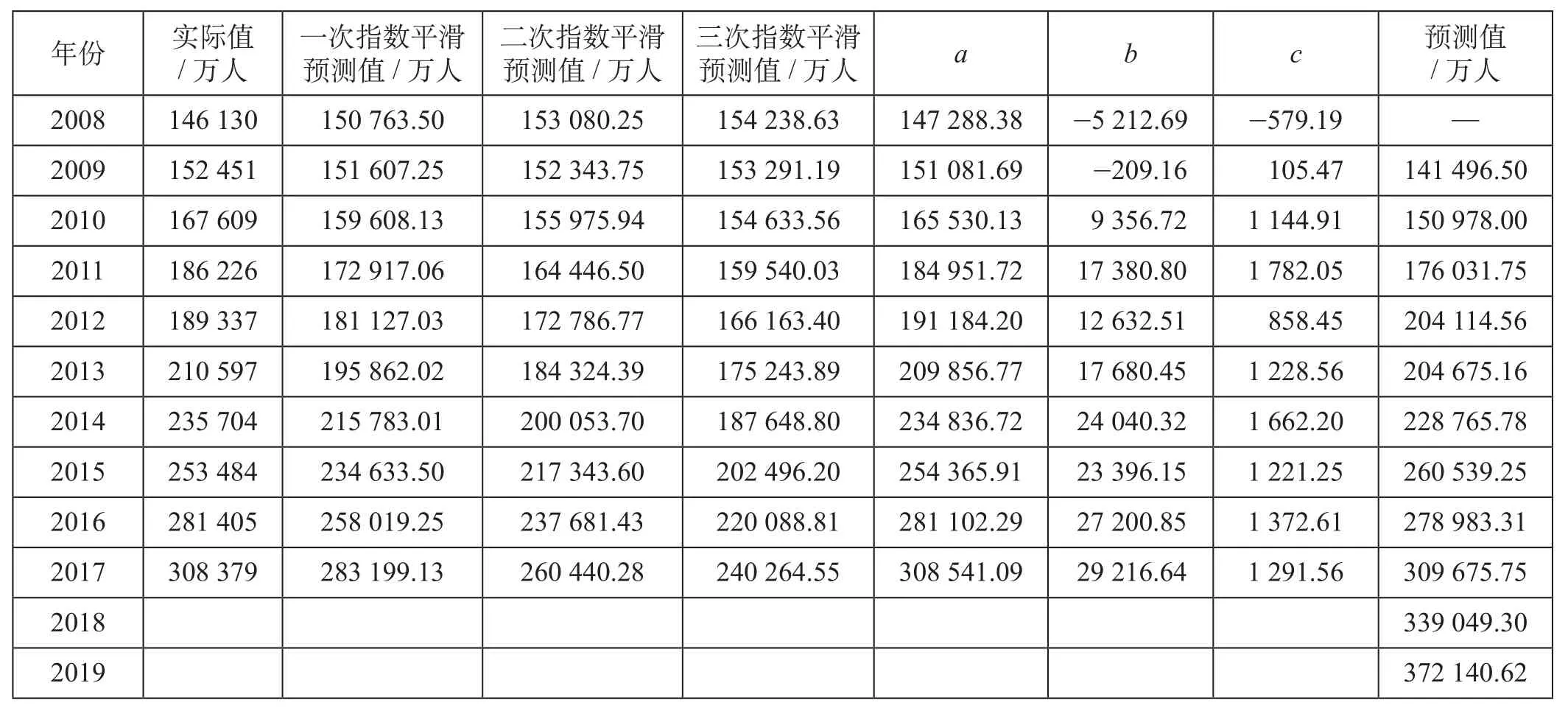
表4 三次指数平滑法预测值Tab.4 Predictive value of cubic exponential smoothing method

由表5可知，实际值与预测值相关系数R= 0.988，表明实际值与预测值显著相关。概率值P = 0.000 ＜0.05，即说明实际值与预测值之间存在显著相关性。

为分析实际数据与预测结果是否有较大的差异性，采用F检验来判断2009—2017年的实际值与预测结果之间的差异性程度。运用Excel对数据进行分析处理，得到实际值与预测值差异性计算表如表6所示。

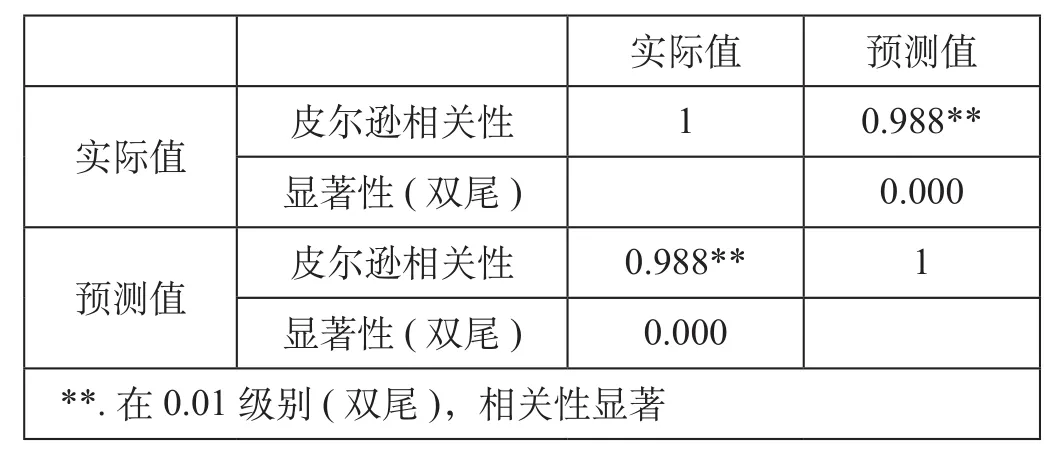
表5 α = 0.05时实际值与预测值相关性计算表Tab.5 Correlation between actual value and predicted value at α = 0.05

表6 α = 0.05时实际值与预测值差异性计算表Tab.6 Difference between actual value and predicted value at α = 0.05

由表6可知，F = 0.008 456，F crit = 4.600 11，F ＜ F crit，表明F值在α= 0.05的水平上不显著，即实际值与预测值在α= 0.05的水平上不存在显著的差异性。由此可知，预测结果与实际数据具有显著的相关性和不显著的差异性，因而预测结果可信度较高。

（2）预测结果精确度分析。从目前已有的实际值与计算出的预测值的误差分析可以得出整体预测误差为4.47%，2016年、2017年实际值与预测值的误差分别为0.86%和0.42%，误差极小，由此可知，采用三次指数平滑法预测铁路旅客发送量具有较高精度。

对于2018年、2019年的预测结果，从预测误差方面看，根据三次指数平滑法的短周期的特点，预测出的2018年、2019年的数据误差应该靠近2016年、2017年的误差，初步判断2018年、2019年2年的预测误差应在1%～5%之间；从预测数字方面看，未来2年的旅客发送量呈现出较为稳定的上升趋势，旅客数量将不断增加，铁路相关部门应该采取相应的措施，保证出行旅客数量与铁路运输能力的匹配，使我国的铁路旅客运输能够安全、健康、有秩序地运行。

3 结束语

铁路旅客发送量的预测是铁路客运部门编制客运计划和制定客运发展政策的基础，是一项具有重要意义的工作。由于铁路旅客发送量的数据具有一定的波动性，铁路旅客发送量的预测往往难以达到绝对精准。将三次指数平滑法模型应用到我国铁路旅客发送量的预测中，避免了其他预测方法冗杂、繁复的问题，且预测结果分析表明，三次指数平滑法预测结果整体上精度较高、效果较好。三次指数平滑法仅仅基于数据对铁路旅客发送量进行预测，而在大多数情况下，铁路旅客发送量是受多种复杂因素影响的，在今后的研究中，应考虑多种主客观因素对铁路旅客发送量预测产生的影响。