RADIAL SYMMETRY FOR SYSTEMS OF FRACTIONAL LAPLACIAN∗
Congming LI(李从明)Zhigang WU(吴志刚)
1.School of Mathematical Sciences,Shanghai Jiao Tong University,Shanghai 200240,China;
2.Department of Applied Mathematics,University of Colorado Boulder,USA;
3.Department of Applied Mathematics,Donghua University,Shanghai 201620,China
E-mail:congming.li@colorado.edu;zgwu@dhu.edu.cn
Abstract In this paper,we consider systems of fractional Laplacian equations in Rnwith nonlinear terms satisfying some quite general structural conditions.These systems were categorized critical and subcritical cases.We show that there is no positive solution in the subcritical cases,and we classify all positive solutions uiin the critical cases by using a direct method of moving planes introduced in Chen-Li-Li[11]and some new maximum principles in Li-Wu-Xu[27].
Key words system of fractional Laplacian;method of moving planes;maximum principles with singular point;Kelvin transform
1 Introduction
This paper is devoted to investigate the symmetry properties for nonnegative solutions of fractional Laplacian system in Rnwith n≥2:

where the given functions f1(u),f2(u), ···,fm(u)are real-valued functions and satisfy the general structural condition for x∈Rnthat

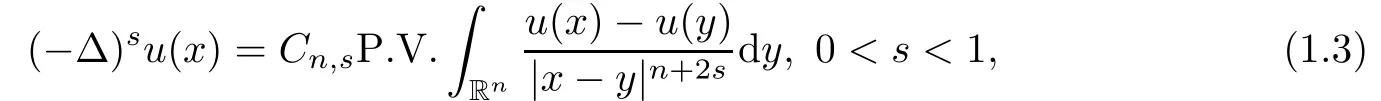
where P.V.stands for the Cauchy principle value.De fine

Then it is easy to see that foris well-de fined for all x∈ Ω.
During the last decades,nonlinear equations involving general integrodi ff erential operators,especially,fractional Laplacian,have been extensively studied since the work of Ca ff arelli and Silvestre[8].Later on,there are many results on regularity and existence of fractional Laplacian equations,we refer readers to[6,7,9,17,31,33,34,39]and the references therein.
When s=1 and m≥2,the first work on symmetric properties of the system(1.1)of Laplacian equations in a bounded ball is Troy[36]when the system is cooperative

Then it was extended by Figueiredo[19]and Sirakov[35]for other kinds of domains like cones,paraboloids,cylinders.Later on,for the whole space,the first result is also in Busca-Sirakov[5]when the system is cooperative,some assumptions on the derivatives of the nonlinear terms to guarantee the system cannot be reduced to two independent systems and the decay conditions of the solution at in finity.And Chen-Li[12]used the equivalence between the system(1.1)and a corresponding integral system to deduce the symmetric properties of the system.In addition,they introduce another natural condition on nonlinear terms that the system is non-degenerate if
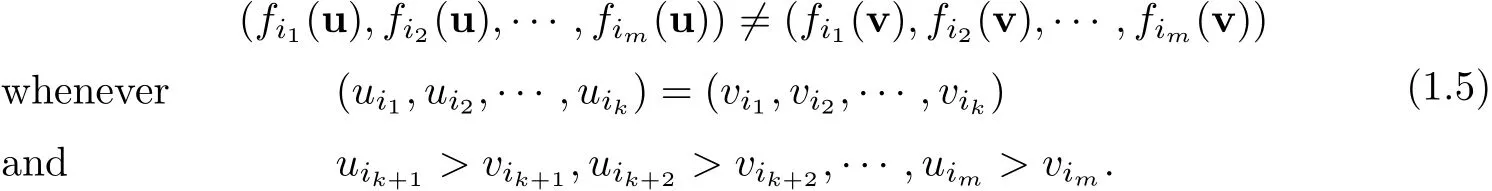
Here i1,i2,···,imis a permutation of 1,2,···,m.This assumption also can guarantee that the system contains no independent subsystem,such as,to avoid a situation like

Obviously,u1and u2may not have the same center,since the two equations are totally unrelated.Recently,Zhuo-Chen-Cui-Yuan[40]showed the equivalence between the system(1.1)with m≥2 and a corresponding integral system for 0<2s

The motivation of the present paper is to extend the results in[11]to the system(1.1),where they develop a direct method of moving planes to the singular equation of fractional Laplacian.In addition,we will re fine the results for the system in[40].In particular,on the one hand,we only need the system is cooperative as(1.4)instead of the assumption(1.7).On the other hand,we need not the assumption that the nonlinear terms are homogeneous with the degree 1in[40].Specially speaking,our assumption(1.2)is general,and we shall give the following examples:

In addition to the previous subcritical and critical cases in[11,40]and references therein,here we give the following de finition to categorize the general critical and subcritical cases.
De finition 1.1For the the system(1.1)with the nonlinear terms fi(u1,···,um),
(i)we say the system is “critical”,ifis independent of t for all x and i=1,···,m;
(ii)we say the system is “subcritical”,if there exist i0∈ {1,···,m}and a point z ∈ Rnsuch that
Notice that for the critical case,we only need
is independent of t when t is near 1,since the case that t is away from 1 is no big deal.Our subcritical case includes the classical subcritical case that the nonlinear termsand our critical case includes the classical critical case that the nonlinear terms
We review some previous results closely related to the topic of the present paper.There are some e ff orts on the symmetry and monotonicity results for equations involving the fractional Laplacian in the unit ball or in Rn.These results are mainly based on the method of moving planes which was introduced by Aleksandrov[1]and developed by Serrin[32],Gidas-Ni-Nirenberg[21,22]and many others.It is difficult to apply the method of moving planes to fractional Laplacian equation due to the nonlocality of the fractional Laplacian.Several methods have been used to deal with this difficulty.The first one is the extension method in Ca ff arelli-Silvestre[8]by transforming the non-local problem to a local one,which was applied to another type of fractional Laplacian equation in[15].The second is to establish the equivalence between the di ff erential equations with the integral equations in Chen-Li-Ou[13],and the method of moving planes for the integral form.Recently,Chen-Li-Li[11]developed a direct method of moving planes to treat the non-local problems in general domains by developing some interesting maximum principles for antisymmetric functions.When m=2,for example see[5,20,28,30]and references therein.
Recently,Cheng-Huang-Li[16]presented a pointwise estimate of(−∆)su at the non-positive minimum point,which is easier to use in the direct method of moving planes to obtain the symmetry properties for the positive solution in bounded domain and unbounded domain in Rn.These results have been extended to the general system case in[26].In[16]and[26],they need the decay conditions at in finity of the solutions because they directly deal with the solutions without using Kelvin transform.
When working on unbounded domains,some previous work made strong assumptions on the asymptotic of the solutions.To avoid these assumptions,we are applying the Kelvin transform here.However,this induces some singularities to the transformed functions.To deal with these singularities,we use the Bˆocher theorems and maximum principles developed in Li-Wu-Xu[27]for fractional super-harmonic functions on punctured balls.Thus,we can classify solutions to general nonlinear systems of critical and subcritical types without any assumption on the asymptotic of the solutions at in finity.
Our main theorem states:
Theorem 1.2Let n ≥ 2,i=1,···,m and s∈ (0,1).Assume thatsolves(1.1)and fi(u)are non-negative,continuous,and satisfy(1.2)(1.4),(1.5)and

Then,
(i)in the critical case,all of uimust have the form

(ii)in the subcritical case,ui≡constant.
The paper is organized as follows.In Section 2,we give some lemmas which will be used in the method of moving plane.Section 3 is devoted to the monotonicity and symmetry properties of the solution of the system(1.1)by using the direct method of moving planes.
2 Preliminaries
As usual,let

be the moving planes,

be the regions to the left and the right of the plane respectively,and

be the re flection of x about the plane Tλ.
Assume that u is a solution of pseudo di ff erential equation(1.1).To compare the values of u(x)with u(xλ),we denote
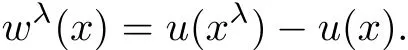
In many cases,wλmay not satisfy the equation

as required in the previous theorems.However one can derive that
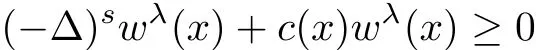
for some function c(x)depending on u.If c(x)is nonnegative,it is easy to see that the maximum principle is still valid;however this is not the case in practice.Fortunately,in the process of moving planes,each time we only need to move Tλa little bit to the right,hence the increment of Σλis a narrow region,and a maximum principle is easier to hold in a narrow region provided c(x)is not “too negative”,as you will see below.
The following pointwise estimate of(−∆)sw at the minimum point is key for our proof.In the rest of paper,we call a function w(x)is λ-antisymmetric function if and only if

Proposition 2.1Let w(y) ∈ L2sbe a λ-antisymmetric function de fined in(2.1).Suppose there exists x∈Σλsuch that

ProofA similar result as in this proposition has been given in[16].For completeness,here we give the proof with minor di ff erences,and obtain the detailed expression of the constant
By the de finition of(−∆)sw(x)we have

In getting the estimate for I1,we use the mean value theorem for t−n−2s,for t∈ (0,+∞).
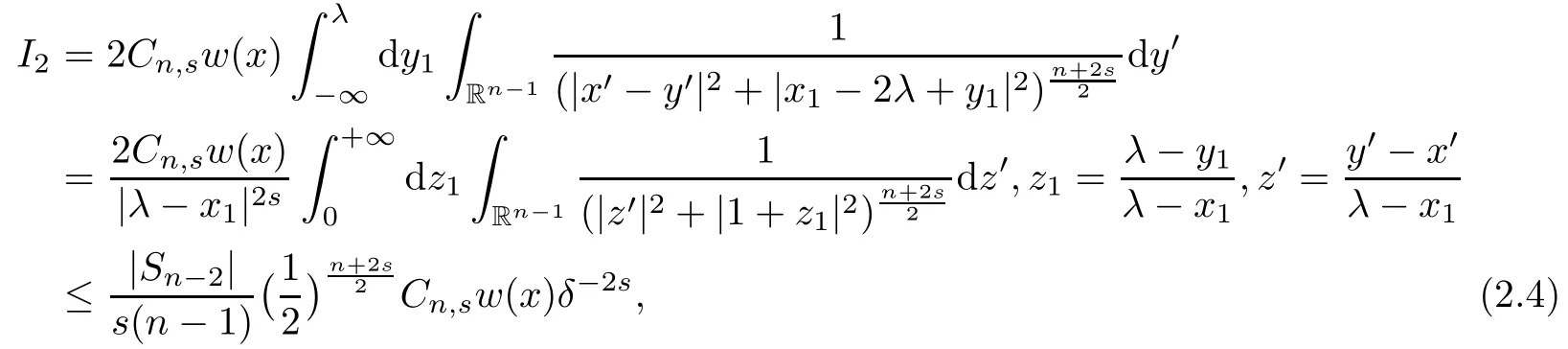
where we have used the following estimate
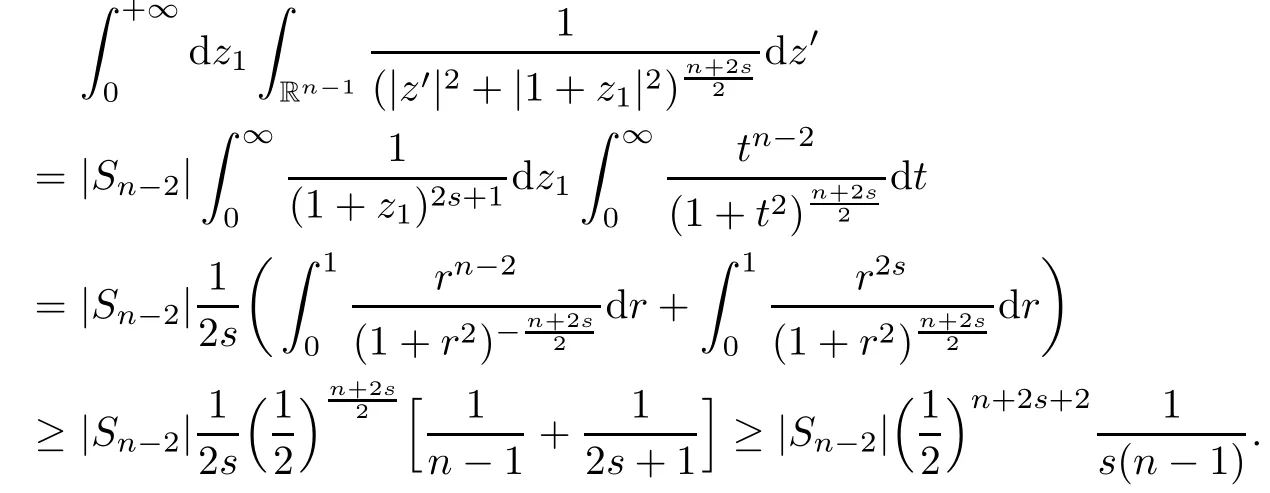
Combining(2.3)and(2.4),we complete the proof of(2.2).
The following two propositions on maximum principles near the singular points are the key ingredients to carry out the method of moving planes and the Kelvin transform.
Proposition 2.2([27]Fractional maximum principle on a punctured ball) Assume that w(x)∈L2s,and satis fies in the sense of distribution that

then there exists a positive constant c=c(n,s)depending on n and s only such that

Proposition 2.3([27]Fractional maximum principle for anti-symmetric functions) Assume that w(−x1,x′)= −w(x1,x′), ∀x ∈ H,and Br(x0)⊂ H,
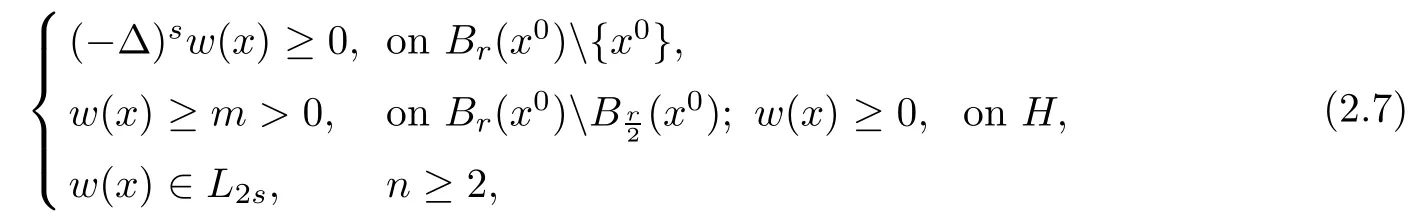
then there exists a positive constant c=c(n,s)<1 depending on n and s only such that

These two propositions are based on the following lemmas in[27].
Lemma 2.4(see[27]) Iffor the domain Ω ⊂ Rnwith n ≥ 1,andthe molli fication
In particular,if letting f(x)=0,when w(x)is nonnegative and fractional super-harmonic(fractional sub-harmonic)in the domain Ω in Rn,then the molli fication wǫ(x)=w ∗ ρǫ(x)is also fractional super-harmonic(fractional sub-harmonic)in the domain Ωǫ.
Lemma 2.5(see[27]Bˆocher theorem for fractional Laplacian) Let v(x)∈ L2swith n ≥ 2 be a nonnegative solution to

3 Symmetry of the Solutions
Because no decay condition on uinear in finity is assumed,we are not able to carry the method of moving planes on uidirectly.To overcome this difficulty,we make a Kelvin transform.
Let x0be a point in Rn,and

be the Kelvin transform of uicentered at x0.Then since fiis homogenous with respect to u1,···,um,it is well-known that

We consider x1-direction,since the other directions can be treated similarly.let
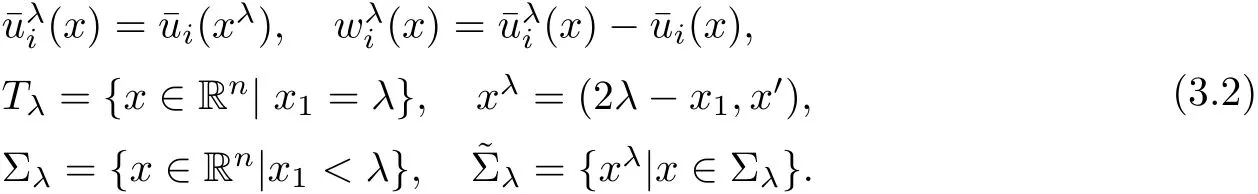
In many cases,w may not satisfy the equation

as required in the maximum principle when using method of moving plane.However one can derive that
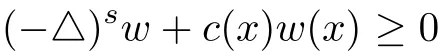
for some function c(x)depending on u(x).Then to use the results in Section 2,we need the following estimates on the fractional Laplacian at the point of negative minimum value,which is used to carry on the method of moving planes.
Lemma 3.1is the point of Kelvin transform and.And assume thatare the solutions to(3.1)and fi(u)are non-negative,continuous,and satisfy(1.4)and
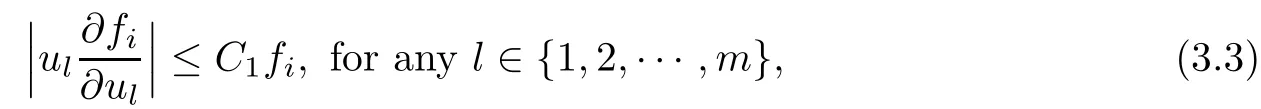
Then

and has the following estimate
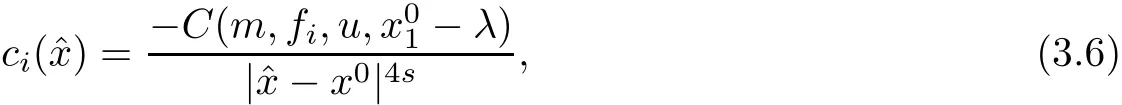
ProofFrom(3.1),we have
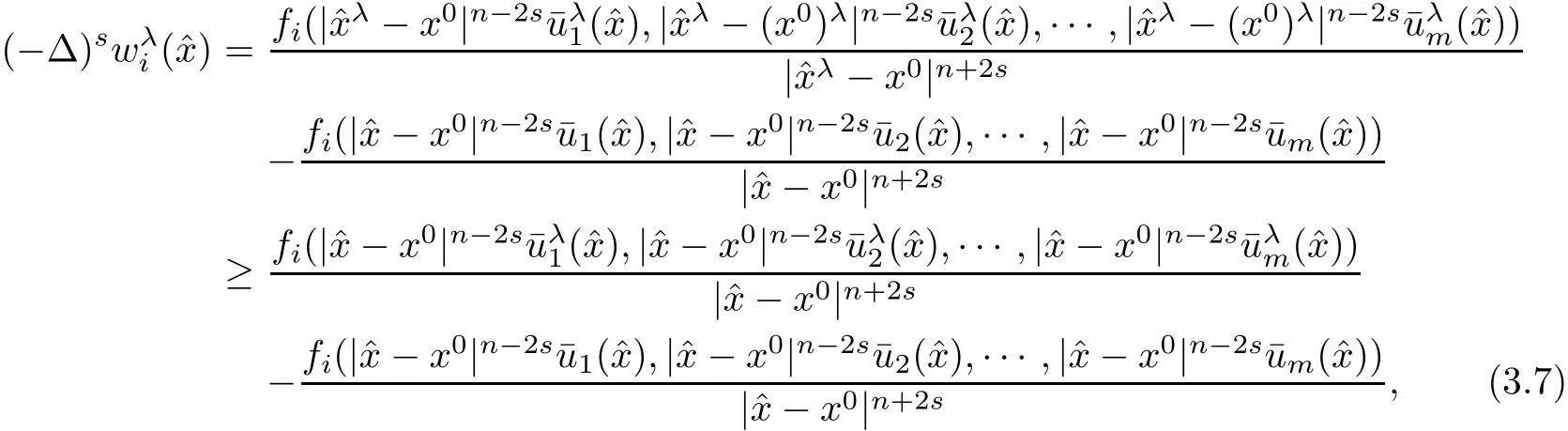
where we have used the assumption(1.2)and the factand
First,we give the proof under the assumption(3.3).For simplicity,we assume that

Then there are two possibilities:
Notice that it must have i∈ {1,2,···,k},which will be used in the possibility(2).
Case(1)From(1),we have

which together with the nonnegativity of fiyields that

Case(2)From the assumption(1.4)and the fact that i∈ {1,2,···,k},we have

Combining(3.8)and(3.13),we have obtained the estimates(3.4)and(3.5)under the assumption(3.3).This proves Lemma 3.1.
First,notice that,by the de finition of,we have
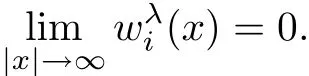
With the above preparations,we can establish the radial symmetry about a center point and strict monotonicity with respect to the radial r about the center via the following steps:
(a)For λ negative large,we show that
(c)We can do the above similar to negative x1-direction or to the function
(d)The steps(b)and(c)imply that¯u is symmetric in the x1-direction about some point,and is strictly monotone with respect to the center.
(e)We can do this for all directions to get the radial symmetry and strict monotonicity with respect to the center.
(f)We show the strictly monotonicity with respect to the radial r.
3.1 Radial Symmetry about a Center Point and Monotonicity
Step 1We do part(a)and show that for λ sufficiently negative,

To this end,we first claim that
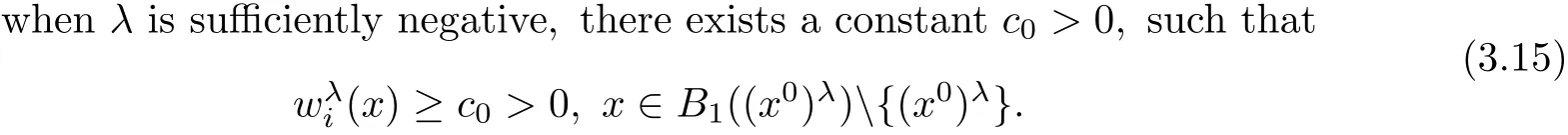

for suitable small c0>0.On the other hand,for,we haveholds
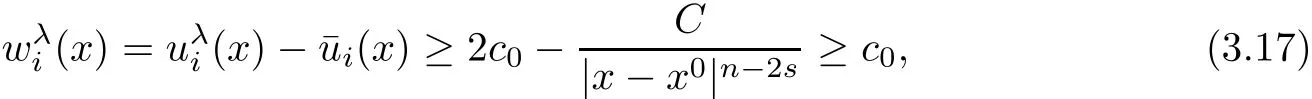
when λ sufficiently negative,that is,x1is sufficiently negative since x ∈ Σλ.This proves(3.15).
Then we can deduce(3.14)using proof by contradiction.
If(3.14)is not true,there exists λk→ −∞ and

From(3.15),we know Akcan only be obtained outsidelarge enough.Hence we must have
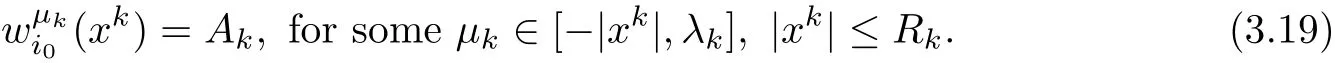

On the other hand,Proposition 2.1 yields
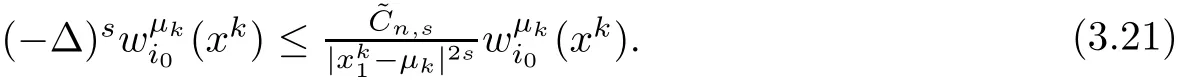
Then combining(3.20)and(3.21),we have

Step 2In this step,we will carry out the step(b)stated above.In fact,step 1 provides a starting point,from which we can now move the plane Tλto the right as long as(3.14)holds to its limiting position.By(3.21),we also know that the negative minimum ofcannot be attained outside of BRo(0)for some fixed R0>0.Next we argue that it can neither be attained inside of BRo(0).
By the de finition of λ0and the continuity of
In this part,we show that either

If(3.23)holds,one can use the method of moving planes from near x1=+∞,and also obtainis symmetric about the Tλ0in x1-direction.Since the other directions can be treated similarly.Hence,we have prove thatare radially symmetric about the point x0.

This is a contradiction with the de finition of λ.Hence we must have

For the convenience of narration in the following,we denote

To prove this contradiction,we go through with the following steps.
Step 2.1We show that


which yields a contradiction.Herein Lemma 3.1 is bounded sinceThis proves our claim(3.29).
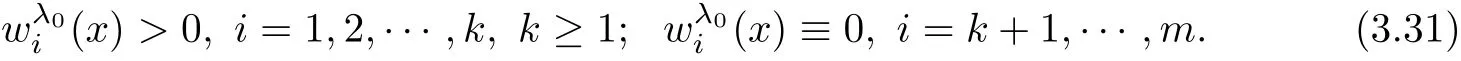
Second,we show that k=m,which leads to
In fact,if k which is a contradiction.This yields that k=m,and we have proved the claim(3.28).Step 2.1 is completed. Step 2.2We prove that there exist a constant c0>0 and a suitable positive constant First,from the continuity ofand the claim(3.28),we know that there exists a constant c1>0 such that Step 2.3We want to show the following holds, Suppose(3.35)is not true,one has where C1is dependent ofbut is independent of ǫ. From the result in Step 1 and(3.36),we know Bkcan be obtained,i.e.,and some Step 3We deduce the radial symmetry and monotonicity by carrying out the steps(c),(d)and(e).First,similar to negative x1-direction,we can work on the positive x1-direction or just work on the functionto get eitherfor some λ0<.Then,we havefor i=1,···,m,that is,all ofare symmetric in the x1-direction about the same point,and is monotone with respect to this center.Second,since x1-direction is chosen arbitrarily,we can obtain the symmetry and monotonicity in the other directions.Hence,we have deduced allare radially symmetric with respect to the same center and monotone with respect to the radial r. Hence,in the following,we prove(3.38). From Theorem 2.1 in[11],we know.Thus,in what follows,we only consider the case that all ofare positive,and prove the strict monotonicity for the positive solution. To this end,we suppose that there exists a δ0>0: The other directions can be treated similarly.Thus,we have proved that all ofare strictly monotone with respect to the radial r. First,we consider the subcritical case,and prove that ui(x)≡constant.Here we still consider the x1-direction to deduce the desired result.To this end,we show that In addition,by using the monotonicity(1.2),we know(4.3)also holds for all t>1. which contradicts(4.2).Similarly,whenwe can also arrive at a contradiction. Finally,when z∈Tλ0,we can choose another pointin a small neighborhood of z such thatThen a same process as above can also yield a contradiction at the point In summary,we have proved(4.1).Therefore,for the subcritical case,we have proved Hence,we can conclude that all of ui(x)(i=1,2,···,m)are symmetric in the x1-direction at.Since the x1-direction can be chosen arbitrarily,we have actually shown thatis radially symmetric about x0. For the critical case,we know that the system(1.1)is invariable under the Kelvin transform.From the fact that the radial symmetry and strict monotonicity ofobtained in Section 3,we can immediately obtain(1.9)by using the classi fication method introduced in[13]. This completes the proof of Theorem 1.2.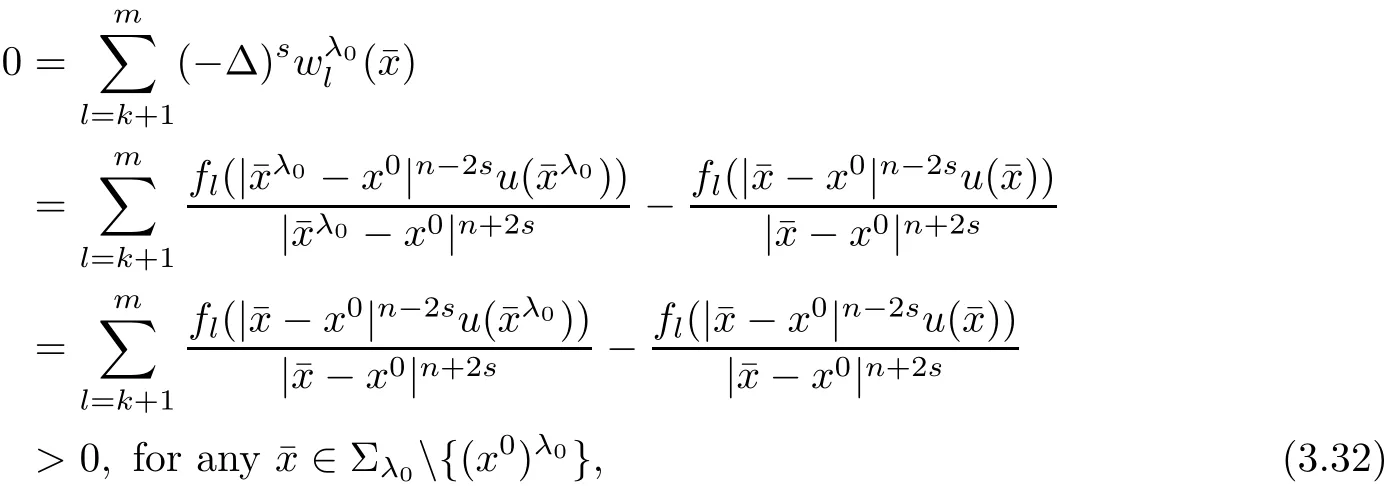
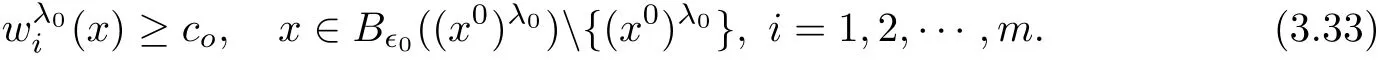





3.2 Strict Monotonicity

4 Proof of Theorem 1.2



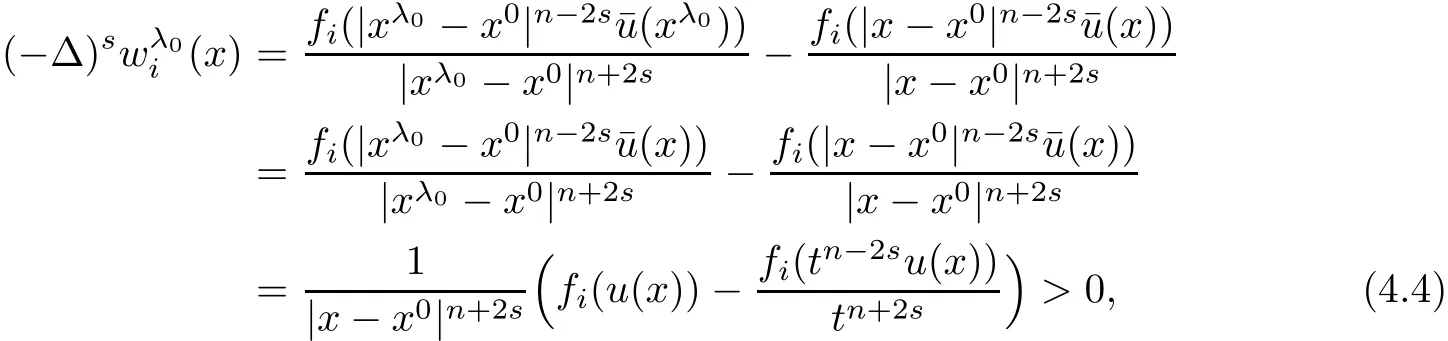

 Acta Mathematica Scientia(English Series)2018年5期
Acta Mathematica Scientia(English Series)2018年5期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARIZATION OF PLANAR VORTICES FOR THE INCOMPRESSIBLE FLOW∗
- YAU’S UNIFORMIZATION CONJECTURE FOR MANIFOLDS WITH NON-MAXIMAL VOLUME GROWTH∗
- STABILITY OF STEADY MULTI-WAVE CONFIGURATIONS FOR THE FULL EULER EQUATIONS OF COMPRESSIBLE FLUID FLOW∗
- ONE-DIMENSIONAL VISCOUS RADIATIVE GAS WITH TEMPERATURE DEPENDENT VISCOSITY∗
- MACROSCOPIC REGULARITY FOR THE BOLTZMANN EQUATION∗
- STRONG COMPARISON PRINCIPLES FOR SOME NONLINEAR DEGENERATE ELLIPTIC EQUATIONS∗
