基于多点序列预瞄的自动驾驶汽车路径跟踪算法研究＊

赵凯 朱愿 冯明月 苏致远 郭宏达

（1.陆军军事交通学院，天津 300161；2.军事交通运输研究所，天津 300161）

主题词：自动驾驶汽车 预瞄信息 路径弯曲度 路径跟踪

1 前言

移动机器人是复杂的非线性系统，且运行于不同的复杂工况下，其路径跟踪问题一直是研究的重点和难点[1-4]。移动机器人所跟踪的路径大致可分为显式（Explicit）和隐式（Implicit）两种，相对于隐式路径，显式路径的基本思想是只需从传感器数据中提取特定路径的基本信息，可大幅降低处理的复杂性，因此多采用显式路径作为目标跟踪路径[5]。为提高移动机器人的路径跟踪能力，Maier D等[6]提出了一种改进的GPS传感器模型来生成城市区域的GPS轨迹地图，并使用全地形机器人检验了模型的合理性。Takai R等[7]将实时动态差分GPS（Real-time Kinematic GPS，RTK-GPS）与惯性测量单元（Inertial Measurement Unit，IMU）结合，用于无人履带式拖拉机的巡线跟踪。

在控制策略的选择上，除传统的PID控制外，考虑当前车辆姿态和跟随路径之间的几何关系亦可提供更简单的跟踪策略[8]。文献[4]中，谢德胜等人采用标准卡尔曼滤波器对受干扰时的RTK-GPS数据进行滤波，用最优估计值作为机器人的真实位置，使用角度偏差PD控制器输出转向，将横向偏差控制在0.67 m以内，但其移动速度仅为2 m/s。Zhang Wenyu等[8]人采用粒度支持向量回归（Granular Support Vector Machine，GSVR）的方法提高了Pure Pursuit算法的适应性和动态性能，使得自主机器人以1.2 m/s的速度跟踪路径时，直线追踪最大横向偏差小于0.088 m。

自动驾驶汽车作为轮式移动机器人的一种，同样存在着路径跟踪这一难题。对此，本文提出了一种基于预瞄信息的路径跟踪算法。车辆接收实时差分GPS数据，确定其在全局坐标系中的位置，根据当前位姿及其与路径间的相对运动关系建立预瞄点序列搜索模型，使用多点预瞄的策略预测路径的曲率变化，并按一定的规则控制车速。另外，将预瞄偏差角作为控制器的输入，通过Pure Pursuit算法计算出前轮转角控制量，用以控制车辆的转向。最后，通过试验平台验证了跟踪算法的有效性。

2 多点序列预瞄信息的获取

路径预瞄信息包括横向位置偏差、预瞄偏差角、路径弯曲度等。对这些信息加以利用能够使车辆更准确地跟踪路径[9-10]。为了获取路径的预瞄信息，首先需建立车辆和路径的相对运动关系模型。

2.1 车辆—路径相对运动关系模型

经简化和抽象，建立的车辆—路径相对运动关系模型如图1所示。其中：EON为全局（大地）坐标系，E轴正方向为正东方向，N轴正方向为正北方向；以车辆后轴中点为坐标原点建立局部（车身）坐标系XO′Y，规定X轴的正方向为车辆前进方向；δ为前轮转角；θ为航向角，即车辆前进方向与E轴的夹角；v为前进速度；L为轴距。

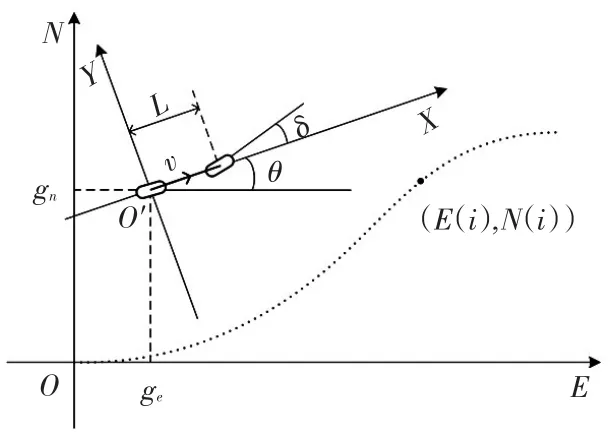
图1 车辆—路径相对运动关系模型

采集到的GPS轨迹实则是一系列有序的经纬度坐标，将其由WGS-84坐标系转换到平面直角坐标系，再将轨迹点序列的起点作为坐标原点（i=1）建立全局（大地）坐标系，GPS轨迹点在全局坐标系下的坐标表示为(E(i),N(i))(i=1,2,…,n-1,n)，i为GPS轨迹点序号。自动驾驶汽车所跟踪的目标路径以上述点序列形式给出。设车辆的后轴中点在全局坐标系下的位置坐标为(ge,gn)，则车辆的运动学模型可表示为：

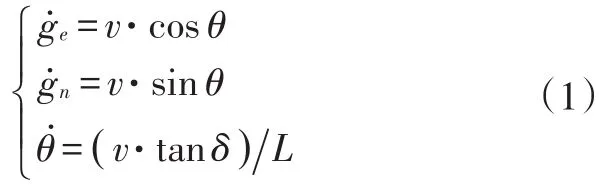
2.2 预瞄偏差角与路径弯曲度

在人工驾驶车辆过程中，驾驶员的眼睛对前方路径不断进行预瞄，根据前方路径的相关信息决定车辆的转弯方向、转角及车速，使车辆尽量逼近前方的路径。对于自动驾驶汽车的路径跟踪控制问题，参考人工驾驶行为，引入路径弯曲度和预瞄偏差角[11]的概念。

假设自动驾驶汽车运动方向与连接预瞄跟踪点和当前位置点的连线的夹角为α，参考文献[9]，定义该夹角为预瞄偏差角（Preview-deviation-yaw）。根据文献[9]的分析可知，路径跟踪的横向控制问题可以转换成预瞄偏差角的跟踪问题。

对于目标路径预瞄跟踪点处曲率变化的描述，本文提出多点预瞄的预瞄策略。除在目标路径上选取一个预瞄点作为跟踪点外，其余预瞄点仅用来描述路径的曲率变化，获取前方路径的弯曲度。首先建立预瞄点搜索算法模型如图2所示，以自动驾驶汽车为参考对象，将GPS轨迹点序列转化到局部坐标系XO′Y中，则轨迹点序列在局部（车身）坐标系下的坐标表示为(X(i),Y(i))(i=1,2,…,n-1,n)：

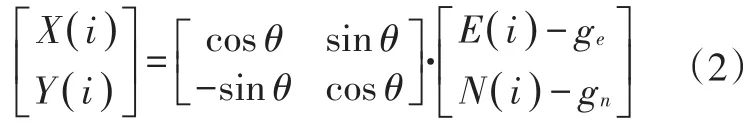
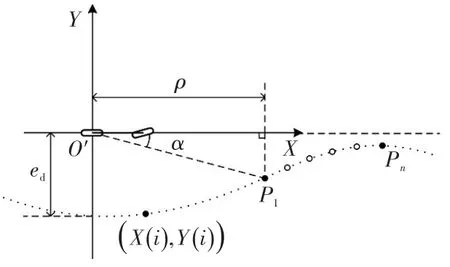
图2 预瞄点搜索算法模型

图2 中，ρ为预瞄距离；ed为横向位置偏差，即当前位置与GPS轨迹之间的距离偏差；Pj(j=1,2,…,n-1,n)为在目标路径即GPS轨迹点序列上获取的预瞄点序列。

搜索预瞄跟踪点P1的步骤为：

a. 由式（2）将GPS轨迹点转化到局部坐标系下；

b.在描述目标路径的GPS轨迹点序列中找出与车辆当前位置距离最近的点，作为本次搜索的起始点；

c. 从起始点开始，沿车身前进方向，在GPS点序列中依次寻找一个点满足：式中，p1为满足式（3）的点在GPS轨迹点序列中的序号。

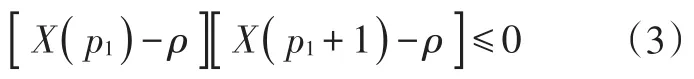
该点即为预瞄跟踪点P1，由此可完成一次预瞄跟踪点的搜索。当车辆运动至新位置时，重复上述步骤，完成一次新的搜索。P1确定后，α随即确定。

人工驾驶行为研究发现，驾驶员主要根据道路曲率的变化控制车速[9]。因此，为了对自动驾驶汽车的纵向速度进行控制，P1确定后，需要寻找其余多个预瞄点Pj(j=2,…,n-1,n)来确定路径的弯曲程度。在局部标系XO′Y中，使用折线表达目标路径的曲率变化比较方便，如图3所示，通过定义路径弯曲度C来描述预瞄点序列处路径的弯曲程度：

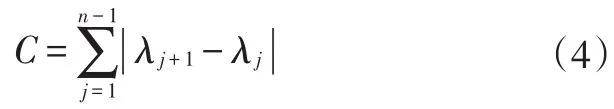
式中，λj为预瞄点Pj(j=1,2,…,n-1,n)处的切线与车辆前进方向的夹角。

|λj+1-λj|的含义是切线角度的相对变化量，用以描述路径曲率的变化，进而表示道路的弯曲程度。路径方向单方向改变或左右摆动变化，路径的弯曲度都在增加。

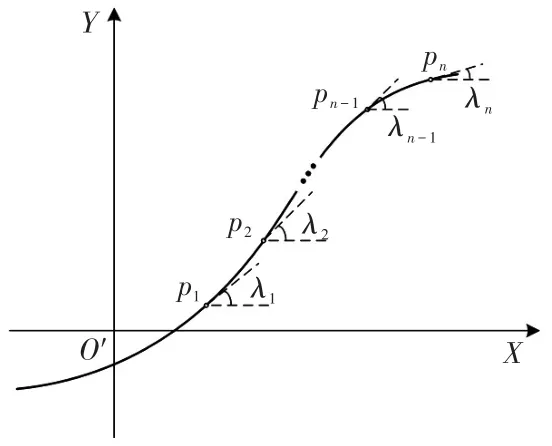
图3 目标路径弯曲度计算示意

其中，Pj(j=2,…,n-1,n)的选取可采用等间隔数选取，即每间隔一定数量的路径序列点选取一个预瞄点。预瞄点之间的间隔数量根据描述目标路径的序列点的“稀疏”程度来选取适当的值，否则不足以表征路径的弯曲程度。可将间隔点之间的欧氏距离之和作为间隔数量的选取指标，该指标应取(1/10～1/8)ρ。

3 基于多点序列预瞄的路径跟踪算法

对于本文研究的自动驾驶汽车系统，控制量主要是前轮转角和纵向速度。自动驾驶汽车的控制系统是一个典型的时延、非线性不稳定系统，而预瞄控制动作具有明显的预见性，从而明显优于传统的依靠信息反馈产生控制动作的控制算法。本文提出的路径跟踪算法框架如图4所示。

3.1 预瞄距离的确定

预瞄距离直接影响路径跟踪的精确性，它的选取至关重要[10,12]。较小的预瞄距离可使车辆更准确地跟踪路径，并能够跟踪更大曲率的路径；较大的预瞄距离可减少跟踪过程中车辆的超调，提高跟踪的平稳性

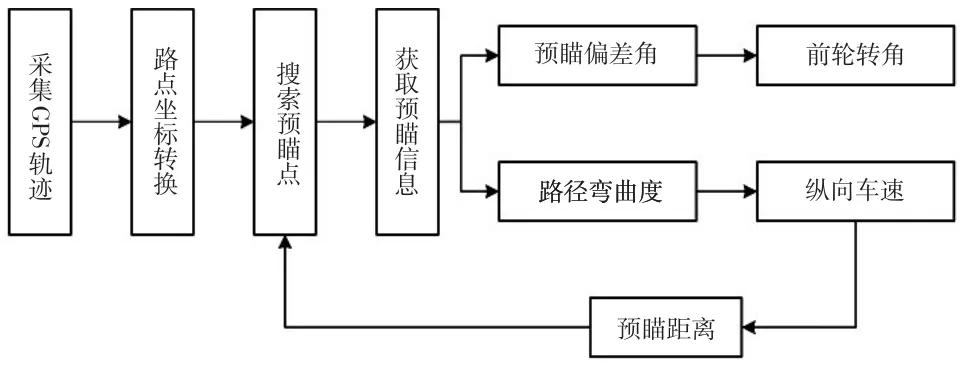
图4 路径跟踪算法框架

为了简化预瞄距离的调优，可按车辆的纵向速度确定预瞄距离[9-10]。此外，预瞄距离通常在最小值和最大值处饱和，因此其与车辆纵向速度之间的关系可用经验公式表示：

式中，lmin、lmax分别为最小、最大预瞄距离；a为常数。

3.2 基于路径弯曲度的纵向控制算法

在局部坐标系下，λj可表示为：

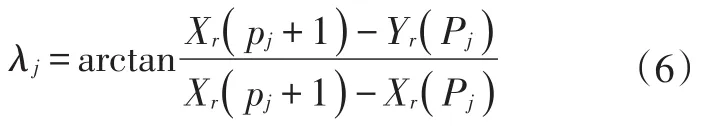
式中，pj为第j个预瞄点Pj在给定的GPS轨迹点中的序号；(Xr，Yr)为预瞄点在局部坐标系下的坐标。

由式（4）、式（6）计算得到路径弯曲度C后，只考虑路径曲率变化对于车速的影响时，基本原则为：C越大，车速v越小；反之，车速v越大。在特定的工况下可能需要车速不超过某个值vmax，因此，为了保证速度v随着路径弯曲度C的增大而显著减小，车速的计算为：

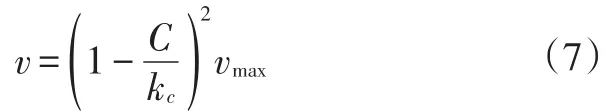
式中，kc(kc＞C)为常数。

在路径给定的情况下，可离线计算出该路径各点处的路径弯曲度C以及整段路径的最大、最小路径弯曲度Cmax、Cmin，则kc的选取范围即为Cmin＜kc＜Cmax。

3.3 基于Pure Pursuit方法的横向控制算法

基于Pure Pursuit的路径跟踪方法是一种几何方法，被广泛应用于机器人的路径跟踪控制[12]。该算法以车辆后轴中点为切点，车辆纵向对称轴为切线，通过预瞄偏差角的几何关系计算前轮偏角δ，使车辆可沿经过预瞄点的圆弧行驶，在这一过程中预瞄偏差角也随之趋于零，如图5所示。

应用正弦定理可得：

式（9）也可以表示为：

式中，ld为当前位置与预瞄点P1间的距离；κ为圆弧曲率。

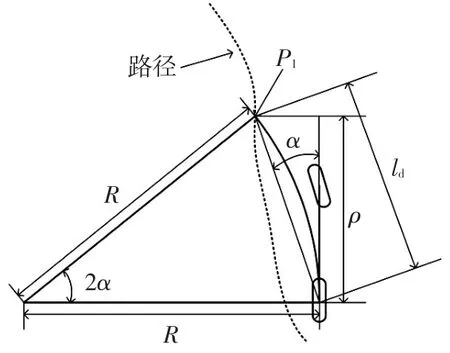
图5 Pure Pursuit算法

根据简化阿克曼车辆模型，前轮转角δ可表示为：

根据式（9）、式（10）可以得到基于Pure Pursuit算法的前轮转角控制量为：

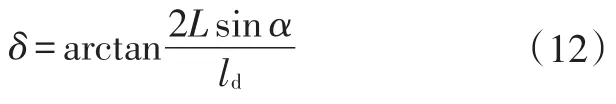
ld=ρcosα，带入式（12）后，便只有1个可调参数，即预瞄距离ρ，这使得算法易于实现和调整。

4 试验验证

4.1 试验平台

采用如图6所示的1∶5缩微自主电动车。该车采用前轮转向、后轮驱动，质量为9.5 kg，轴距58 cm，轮距40 cm，最小离地间隙为6 cm。主控计算机采用NVIDIA的Jetson TX2，最高主频2 GHz，搭载Ubuntu系统，采用Python作为编程语言。自行设计了接口和控制电路，产生脉冲宽度调制（Pulse Width Modulation，PWM）信号控制舵机和电子调速器，实现差分GPS数据转串口输出、主控计算机和底层的通信，以及为差分GPS板卡和主控计算机供电。

图6 缩微自主电动车

4.2 试验结果及分析

首先利用试验平台的遥控功能，操控缩微自主电动车在校园开阔地带采集了具有代表性的直线和“S”形差分GPS轨迹点序列作为目标路径。结合3.1节对于预瞄距离选取的分析，设定最小预瞄距离lmin=2 m，最大预瞄距离lmax=7 m，常数a=1.2。差分GPS的更新频率为20 Hz，故设控制周期T=0.05 s，最大车速vmax=5 m/s，常数kc=4。车辆通过$GPRMC的报文数据确定自身在全局坐标系中的位置、航向和速度。

4.2.1 路径跟踪效果分析

目标路径序列点以GPS轨迹点的形式给出。在GPS轨迹采集过程中，人工操控不稳定以及GPS信号受到干扰等因素使得所采集的轨迹点不够平滑，增加了控制的难度。图7所示为所采集的目标路径和缩微电动车以5 m/s的速度跟随目标路径的结果。车辆在初始位置时，相对于目标路径有较大横向位置偏差，在跟踪过程中，车辆迅速跟踪上目标路径，同时也能克服目标路径不平滑带来的不良影响，跟踪轨迹非常平滑。

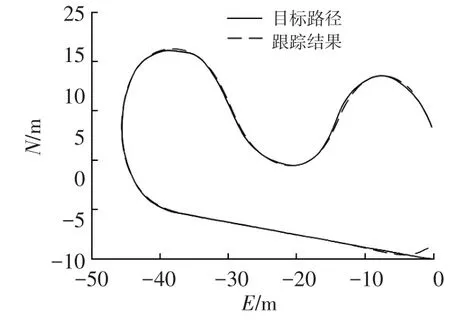
图7 路径跟踪结果

4.2.2 横向控制偏差分析

图8所示为路径跟踪过程中的横向位置偏差曲线。试验结果表明，车辆在直线形路段的路径跟踪横向位置误差可以控制在0.05 m以内，在曲率较大的“S”形路段，横向位置偏差较大，但也可以控制在0.29 m以内。不过，从图7可以看出，目标路径本身不够平滑，使得弯道段的横向位置偏差计算结果偏大。

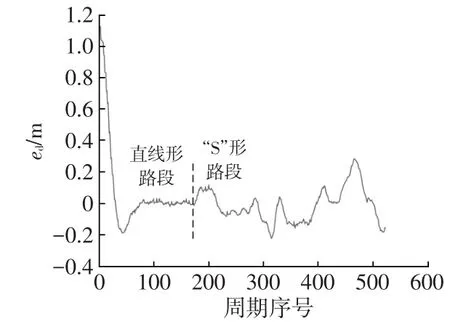
图8 横向位置偏差

4.2.3 跟踪平稳性分析

图9所示为通过Pure Pursuit算法得到的前轮转角控制量，可以看出，本文的横向控制方法得出的前轮转角控制量平滑，这使得车辆在跟随过程中，舵机不会出现较大抖动，跟踪更加平稳。

图10所示为车速v和路径弯曲度C的试验结果，两者的关系满足式（7）的控制规则。车辆直线段基本保持匀速运动，在进入弯道时提前减速，并能随路径弯曲度的增大而减小，既保证了车辆在转弯时减低速度又能保证所有时刻的速度都不超过最大限定速度。由此可见，本文提出的方法对于车辆在纵向速度的控制是有效的。

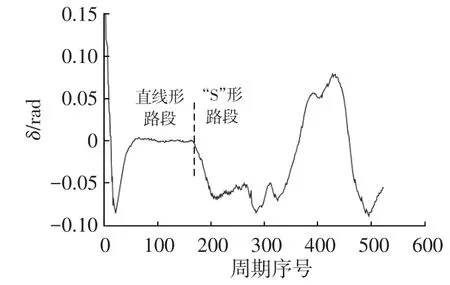
图9 前轮转角控制量

图10 速度与路径弯曲度

5 结束语

本文针对自动驾驶汽车的路径跟踪问题，通过在目标路径上提取多个预瞄点来获取路径的预瞄信息，按C-v关系模型进行自动驾驶汽车的纵向控制，基于Pure Pursuit方法建立了横向控制模型，从而实现了车辆的纵、横向控制。试验结果表明，车辆在跟踪具有代表性的直线和“S”形路径时，可将横向位置偏差控制在0.29 m以内，其中直线段的横向偏差可以控制在0.05 m以内，验证了所提方法的有效性以及合理性。

采用上述方法的自动驾驶汽车纵、横向综合控制，在实现准确路径跟踪的同时，还保证了车辆行驶的平稳性。目前，该方法在研究和试验过程中忽略了转向滞后的问题，下一步将考虑引入预测步骤加以解决。对于更高速度下的适应性也需要进一步研究和验证。