压水堆核电站除氧器保压逻辑优化分析研究
徐志辉, 刘道光,项洪一
(中广核工程有限公司,广东 阳江 529941)
0 引言
某核电站采用压水堆技术,其除氧器压力控制系统基于非安全级数字化控制系统(HOLLIAS-MACS6)实现。除氧器压力控制关系到一回路和二回路的稳定。在机组瞬态响应过程中,其控制回路逻辑组态正确、各项参数合理是对控制系统的基本要求。
3号机组30%满功率(full power,FP)平台跳机不跳堆试验(验证汽轮机跳机后反应堆控制系统将机组主要参数维持或回调至正常运行区间的能力)过程中,除氧器保压逻辑触发滞后,除氧器内压力快速下降,主给水泵出现反转信号,未能实现保压功能。经分析,除氧器主蒸汽进气调节阀的保压逻辑组态存在计算缺陷。该缺陷会增大拒动风险。
本文在现有HOLLIAS-MACS6平台特性的基础上,构建了包含一阶惯性单元、微分单元等模块在内的优化数学模型,给定优化模型中惯性时间参数的选择原则,并依据Simulink仿真和现场测试验证了算法的可行性。
1 保压逻辑控制原理及其风险分析
1.1 保压逻辑原理
保压逻辑控制原理[1]如图1所示。除氧器内的压力,一方面用于保证除氧器正常工作,另一方面用于保证主给水泵入口有一定的吸入压头,以防止主给水泵汽蚀。汽机在20%~100%FP范围内甩负荷时,从高压缸来的抽汽量会突然下降。为了确保除氧器内的压力满足主给水泵吸入压头的要求,需要有主蒸汽进入来维持除氧器压力,使得除氧器压力下降速率能为主给水泵所接受。当除氧器压力下降速率高于0.25 MPa/min时,保压逻辑触发,除氧器主蒸汽进汽调节阀立即全开,维持除氧器压力稳定在0.17 MPa左右,保证主给水泵入口有一定的吸入压头,以防止主给水泵反转和汽蚀。
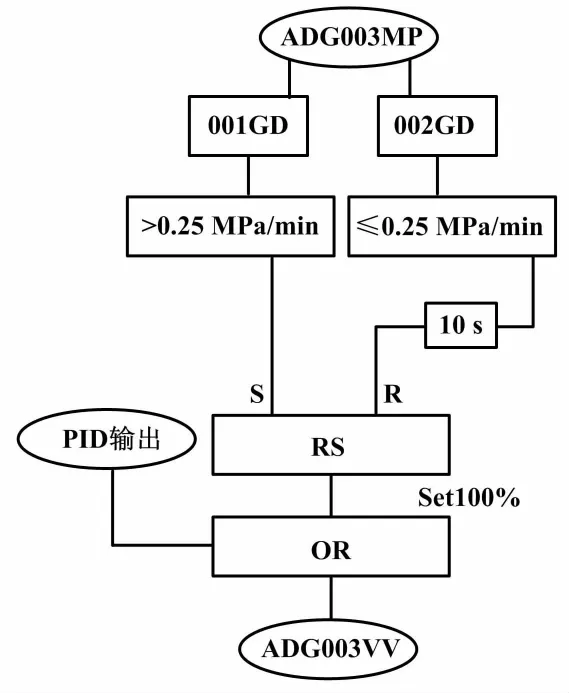
图1 保压逻辑控制原理图
图1中:ADG003MP为现场压力测点;GD为阀值比较;RS为触发器;ADG003VV为阀门开度指令。
1.2 保压逻辑风险分析
①保压逻辑拒动风险分析。
跳机后如保压逻辑未触发或触发延迟,则除氧器内压力迅速下降的趋势就不能得到缓解,主给水泵可能出现反转和汽蚀,同时除氧器内液位会因闪蒸而快速上升。液位的快速上升会导致除氧器给水隔离阀关闭。给水隔离阀关闭之后,除氧器液位又会快速下降,存在引发给水泵跳闸风险,需再次开启给水隔离阀。给水隔离阀的再次开启需要前置调节阀全部关闭,且隔离阀的突然打开,很可能引起凝结水泵出口压力以及喷淋水压力低,喷淋水压力低于定值后会触发凝汽器故障信号,如叠加P10(2/4 功率量程中子通量测量值超过定值)信号,会产生自动停堆信号,导致反应堆停堆。
②保压逻辑动作风险分析。
针对保压逻辑触发后的风险[2-6],在全范围模拟机上对其进行验证,模拟工况及验证结果如下。
在线性负荷变化试验降负荷过程中,使除氧器主蒸汽进汽调节阀全开,一回路因此过冷,温度调节棒没有继续下插反而上提;降至目标负荷后,使除氧器主蒸汽进汽调节阀关闭。因为主给水流量控制系统控制缺少除氧器这部分常规岛分量,导致主给水流量控制系统阀门关小,再加上压水效应,蒸汽发生器液位最低降至-0.95 m。
在停堆试验中,使除氧器主蒸汽进汽调节阀在停堆后全开,此时一回路的剩余热量无法满足除氧器主蒸汽进汽调节阀全开带走的热量,导致一回路过冷,压力快速下降几近失控。紧急关闭主蒸汽系统主蒸汽隔离阀才遏制压力下降。
根据以上模拟机验证的结果可知,保压逻辑触发后,除氧器主蒸汽进汽调节阀的快速开启会导致一回路过冷,存在超功率的风险,同时会引起主给水流量控制系统、蒸汽发生器水位的扰动,在低功率时影响更大。这给机组的控制和安全带来很大的不确定性。
保压逻辑控制回路是否合理尤为关键,既要避免拒动风险,也要避免误动风险。
2 保压逻辑组态优化
2.1 优化前保压逻辑组态缺陷分析
优化前保压逻辑组态等效图如图2所示。

图2 优化前保压逻辑组态等效图
采用HOLLIAS-MACS6平台的梯度模块计算速率,是使用最小二乘法计算一段时间内的压力散点的趋势,并拟合成一条直线。但该梯度模块在保压逻辑处理过程中不是按每秒计算,而是以ΔT的采样周期计算采集时间T,然后每隔T时间输出一次变化,且原则上T越大越好。虽然可以减小“最小二乘法”计算时间,但T设置较短时,若压力值发生突变,梯度模块采样数量会不足,基于最小二乘法的计算原理,会使突变点贡献过大,导致斜率增大,增加误触发保压逻辑的风险。
现场组态中,梯度模块统计周期设置为60 s,采样周期为2 s,则每60 s模块才能输出一次压降斜率计算值,存在明显的控制滞后问题,也是导致本次事件发生的原因。
2.2 保压逻辑的组态优化
优化后的保压逻辑组态等效如图3所示。图3中:MUL为乘法;F01为惯性环节;DIEF为微分环节;DIV为除法。
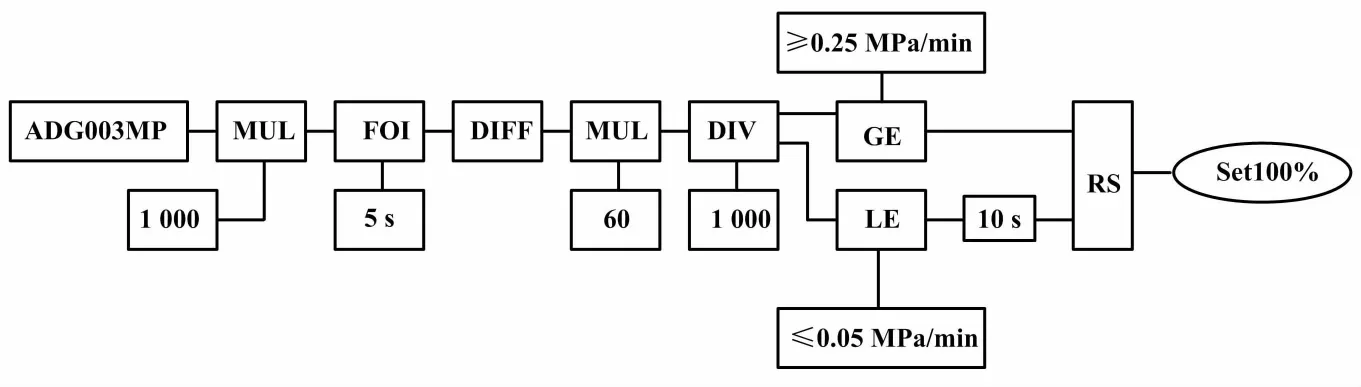
图3 优化后保压逻辑组态等效图
优化后组态方案的选择依据如下[7-8]。
①HOLLIAS-MACS6平台中,微分环节(DIFF)能以秒为单位实时计算斜率,但模拟图中两个定值均按照每分钟的压力变化来实现。设计定值与数字化控制系统分布式控制系统(distributed control system,DCS)组态二者之间必然存在一个转换关系,同时因为压力测量仪表是非线性的,采用秒来处理最终数据显然是不合适。新的组态方案在阈值模块判断之前乘以60,仍以每分钟为计算单位,这样既满足设计要求,又符合现场实际。
②因HOLLIAS-MACS6平台中微分环节是按秒计算的,在组态实时还要对kPa/s与MPa/min的对等性进行处理,即确保压力测量值瞬时下降速率超过0.25 MPa/min对应的4.17 kPa/s时不会触发保压逻辑。因此在优化后的组态方案中增加了一阶惯性环节,它使输出有数秒的滞后,不会出现下降速率一超过4.17 kPa/s就触发保压逻辑的问题。
3 基于SIMULINK的仿真模型验证分析
针对方案中数学模型的响应特性,基于Simulink仿真平台搭建仿真模型。仿真方案如图4所示。依据现场压力仪表的实测数据,分析一阶惯性时间参数变化对惯性加微分模型响应的影响。仿真测试结果如图5所示。由图5可知,加入一阶惯性环节后有明显的消除毛刺、引入滞后作用,且一阶惯性时间越大,对斜率的计算结果的滞后、失真作用越大,故一阶惯性时间不宜过大,考虑前述滞后作用的必要性,在3~5 s内较为合适。
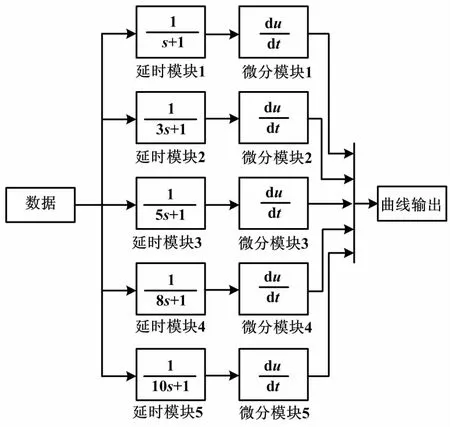
图4 仿真方案图
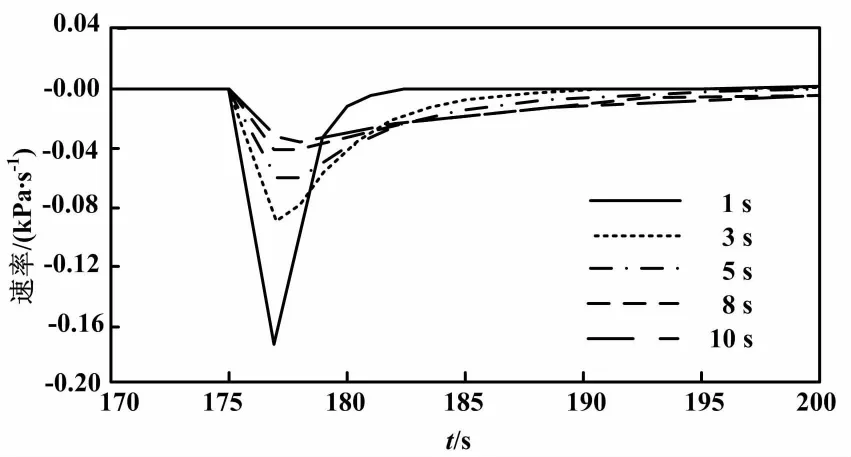
图5 仿真测试结果
4 现场阀门实际动作验证
试验前多次观察了现场压力仪表实测数据在不同工况下的变化情况,得出其波动特性为:压降不是平稳下降,而是以某一斜率下降,且下降时间大于1 s,小于1 min。选取了30%FP平台跳机不跳堆期间,保压逻辑触发时段的实测压力数据如图6所示。

图6 实测压力数据曲线
综合上述,可以确定一阶惯性环节加微分环节参数选择原则应是抖动的瞬时斜率变化超出限值时不触发保压逻辑,而宏观斜率超过限值时,及时触发保压逻辑。因此,一阶惯性环节加微分环节的参数选取需要依据该数学模型其本身响应特性及实测压力波动特性共同确定[9]。
试验按一阶惯性时间分别设置为3 s、4 s、5 s,采用图6中现场压力仪表的实测数据进行现场试验,观察阀门的真实响应。
响应曲线如图7所示。结合现场试验情况以及观察到的压力波动特征,为避免压力变化时响应滞后较多可能带来拒动风险,保守起见选取了如图7所示惯性时间为5 s时的试验结果:压力下降较快时15 s全开,较慢时56 s全开。
在后续的50%FP平台跳机不跳堆及100%FP平台跳机不跳堆试验中,优化后的保压逻辑适当控制,在PID调节参数的配合下,实现了多种复杂瞬态工况下除氧器压力的稳定控制。在现场阀门换型及工况不同时,只需要微调惯性时间即可。

图7 响应曲线图
5 结束语
针对瞬态试验过程中保压逻辑组态缺陷进行了研究,通过DCS平台特性分析、Simulink平台仿真验证,提出了优化组态处理方案。通过现场实际验证确定了最终处理方案,试验结果满足机组运行要求。保压逻辑组态的优化对于了解设计意图与组态实现之间转换的关键点以及确保机组的稳定运行都有着十分重要的意义。

