聚酰亚胺短纤维线密度与拉伸强度的概率分布分析*
1.湖南工程学院纺织服装学院,湖南 湘潭 411104;2.湖南永霏特种防护用品有限公司,湖南 湘潭 411101;3.深圳微纳先材科技有限公司,广东 深圳 518035
聚酰亚胺为主链上含有酰亚胺环的一类聚合物,其具有良好的热氧化稳定性、阻燃性能、高低温性能、力学性能、耐辐射性能和绝缘性能,以及较好的化学稳定性[1]。因其综合性能优良,众多学者对其制备工艺[2-5]、结构与性能[6-10]等进行了较为深入的研究,但对纤维的线密度和强度方面的研究相对较少[11]。
因加工和使用过程中纤维内部和表面存在随机分布的缺陷,导致纤维的拉伸强度表现出一定的随机性和分散性。同时,纺丝过程中因原料性能和工艺参数的波动,将导致纤维的线密度也呈现一定的波动[12]。目前,在表征纤维线密度和拉伸强度时,通常采用多次测试结果的平均值,其建立于纤维线密度和拉伸强度的离散分布规律符合正态分布的假设。前期研究[11]发现,聚酰亚胺短纤维的线密度和拉伸性能指标均呈现偏态分布特征,因而采用平均值来评价纤维的线密度和拉伸性能指标值得讨论。
基于此,为了深入研究聚酰亚胺短纤维的线密度和拉伸强度的分布特征,本文基于原位测量法对3种聚酰亚胺短纤维的线密度和拉伸强度进行了测试,并采用分布模型从统计学的角度对线密度和拉伸强度的离散程度进行了分析。
1 试验对象及方法
1.1 试验样品
本文以甲纶(Suplon©)短纤维和P84短纤维(江苏氟美斯环保节能新材料有限公司提供,工业级)以及轶纶(Yilun©)短纤维(深圳微纳先材科技有限公司提供,民用级)为试验对象。
1.2 纤维线密度
参考GB/T 16256—2008《纺织纤维 线密度试验方法 振动仪法》,在XD-1型振动式纤维细度仪上测试纤维线密度。将试样随机分成50等份,每等份中随机选取1根纤维进行测试,夹持隔距为20 mm,预加张力为0.35 cN。
1.3 纤维拉伸强度
参考GB/T 14337—2008《化学纤维 短纤维拉伸性能试验方法》,采用XQ-1型纤维强度仪,对线密度测试后的纤维进行拉伸强度测试,以做到原位测量。为减少因张力夹更换而导致测量区域改变,尽可能做到线密度和拉伸强度的测试区域一致。纤维拉伸强度测试时,预加张力和夹持隔距与线密度测试时保持一致,均为0.35 cN和20 mm,加载速度为40 mm/min,有效测量样品为50个。
所有测试均在标准大气条件下进行,测试前试样在标准大气条件下平衡24 h。
2 试验结果与分析
2.1 试验结果
3种聚酰亚胺短纤维的线密度以及原位测量获得的拉伸强度分布见图1和图2。由图1和图2可知,3种纤维的线密度与拉伸强度均呈现一定的离散性,且多数频数不集中在中央位置,即呈现不对称分布特征,因而采用正态分布来描述纤维的线密度和强度分布是值得讨论的。
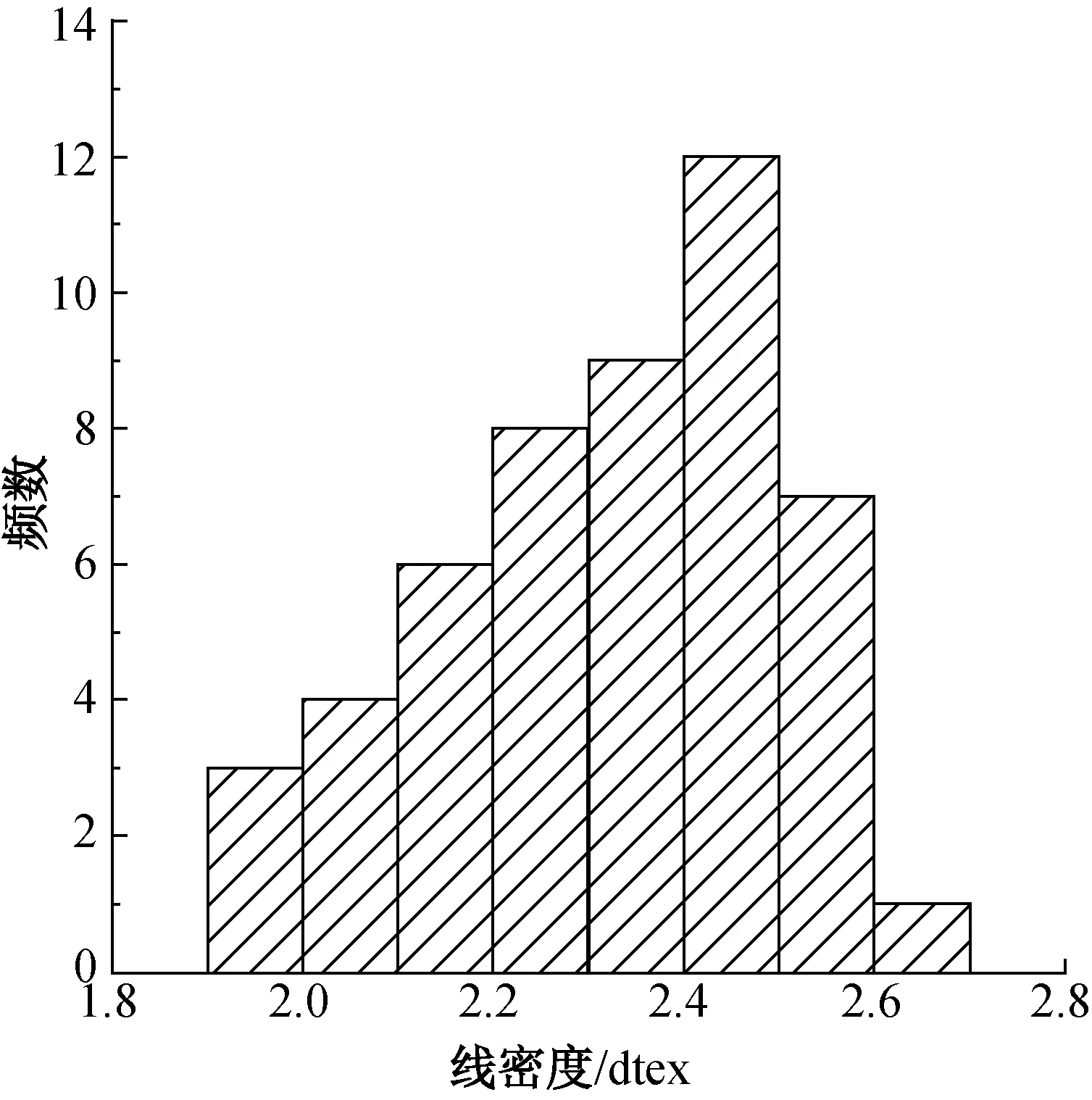
(a) Suplon©

(b) P84

(c) Yilun©

(a) Suplon©
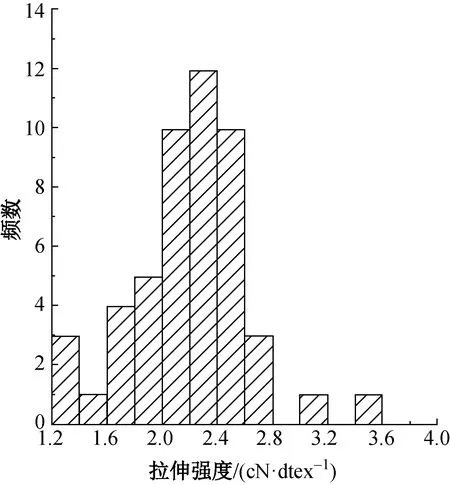
(c) Yilun©
2.2 数据处理
当变量x(x≥0)服从均值为μ(μ>0)、标准差为σ(σ>0)的正态分布时,其累计分布函数FN(x)可表示为:
(1)
式中,Ф为拉普拉斯算子。
在基于“弱环理论”串联模型建立的Weibull分布模型中,两参数Weibull分布模型和三参数Weibull分布模型在纤维、纱线拉伸强度或强力分布的描述时应用最为广泛[13-17]。
三参数Weibull分布模型同时具有位置参数γ(γ≥0)、尺度参数β(β>0)和形状参数α(α>0),通常可较好地拟合正态和对数正态分布,并与正态分布之间存在解析关系[18]。当变量x符合三参数Weibull分布时,累计分布函数F3P(x):
(2)
当γ=0时,三参数Weibull分布简化为两参数Weibull分布,其累计分布函数F2P(x):
(3)
两参数Weibull分布模型可利用概率图法进行模型参数的估计,而三参数Weibull分布模型,因同时存在3个模型参数,其参数估计具有相当的难度,通常采用极大似然法、双线性回归法、概率权重矩法、相关系数优化法以及灰色估计法等,不同的参数估计法其适用范围和精度存在差异[19]。
为便于模型参数的估计,本文基于实测数据,采用Easyfit数据分析软件对分布模型进行参数估计,并基于K-S检验法对分布模型的拟合优度进行检验。数据分析软件对实测数据进行拟合时,自动获得表征拟合优度的p值。通常,通过比较p值与显著性水平a之间的大小关系来判断选用分布模型接受与否。当p
2.3 分布拟合结果
3种短纤维的线密度和拉伸强度的拟合参数及p值列于表1和表2中。从拟合优度的角度而言,本文选用的3种分布模型在描述纤维线密度和拉伸强度分布时的p值均大于0.05,可认为上述分布模型均可用于描述聚酰亚胺短纤维的线密度和拉伸强度概率分布特征。但从拟合最优的角度而言,Suplon©短纤维的线密度分布采用两参数Weibull分布最为合理,而P84和Yilun©短纤维的线密度分布采用三参数Weibull分布最为合理;Suplon©和Yilun©短纤维的拉伸强度采用两参数Weibull分布最为合理,而P84短纤维的拉伸强度采用三参数Weibull分
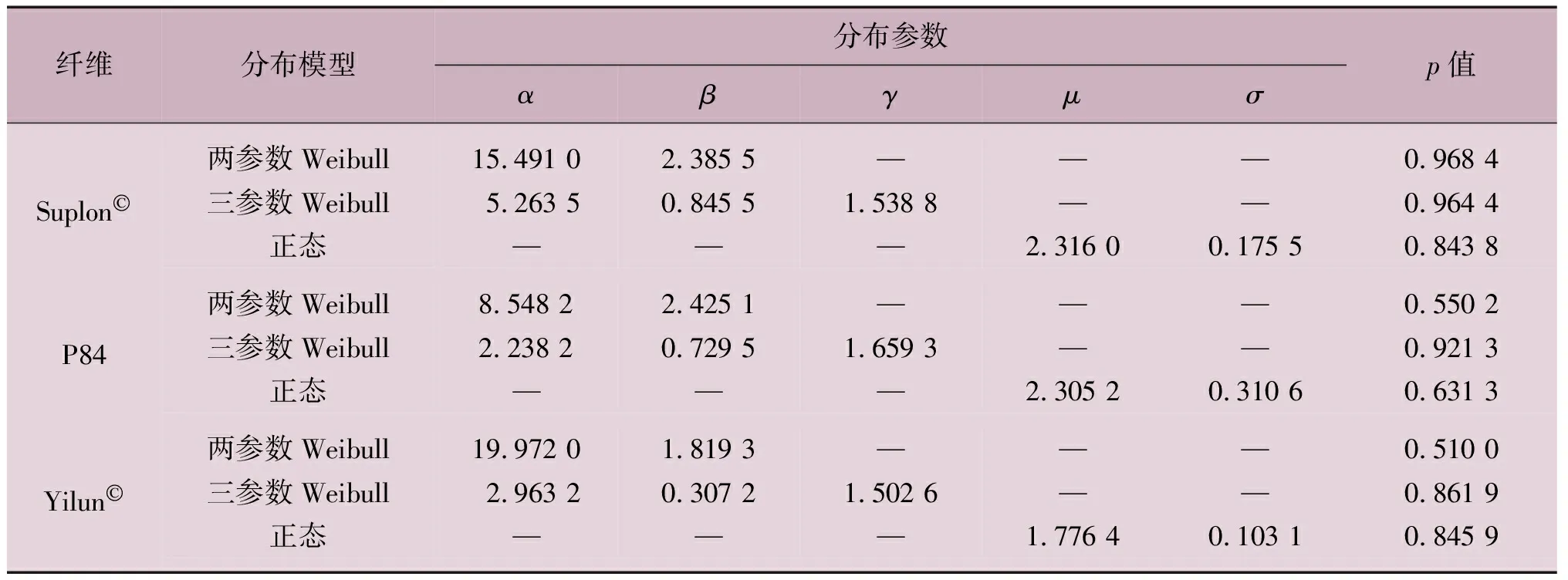
表1 线密度分布参数估计

表2 强度分布参数估计
布最为合理。
值得关注的是,拟合数据是分布模型的最基本条件,Weibull认为随机变量的分布函数并无任何理论基础,通常基于选用的分布模型函数进行参数估计并检验拟合优度,直到找不到一个更好的模型函数为止[20]。故在研究分布模型时,均以获得最佳的拟合优度为基础,提出或修正某一分布模型。因此,如何选择既有理论基础,又具有较好拟合优度的分布函数,值得深入研究。
3 结论
本文基于原位测量法,对3种聚酰亚胺短纤维的线密度和拉伸强度进行了测量,并对纤维线密度和拉伸强度的概率统计分布进行了拟合分析和检验分析。结果表明:Suplon©短纤维的线密度和拉伸强度分布采用两参数Weibull分布描述较为合理,P84短纤维的线密度和拉伸强度分布采用三参数Weibull分布描述较为合理,而Yilun©短纤维分别采用三参数和两参数Weibull分布来描述其线密度和拉伸强度分布较为合理。
——拟合优度检验与SAS实现

