基于流固耦合的复杂血管内血液动力学数值模拟及血管支架有限元分析

袁俊杰，郭无极，王锦涛

（1.广西大学机械工程学院，广西 南宁530004；2.南京农业大学工学院，江苏 南京210031）

0 引言

随着血管支架植入术成为心脑血管疾病的一种重要治疗手段，在植入血管支架后，血液与血管支架之间会发生相互作用，血液的流动会因为支架的存在和血管形状的不同而发生变化，所以研究血液在复杂血管内流动的情况，以便得出血液流动对于血管支架强度的影响变得尤为重要。赵军伟等[1]通过解剖试验建立了二维弹性动脉瘤血液动力学模型，运用fluent与ANSYS相结合研究了血液动力学参数与动脉瘤形成、生长、破裂之间的关系；王彦鹏[2]从固—液两相流的角度，运用血液动力学和计算流体力学的方法和理论对人体心血管系统进行动力学析；石更强等[3]采用UG建立支架和血管模型，将血液作为牛顿黏性流体，运用CFX和ANSYS软件，分析一种菱形血管支架植入血管后，管内流速、应力和压力等参数的变化。文献[4]表明血液流动过程中所产生在内皮细胞上的应力与支架的存在息息相关。

本文为了研究两种复杂形状的血管在不同位置发生病变时，植入支架后，血液的流速变化、管内压力变化，以及二者对于血管支架结构强度的影响，建立了不同形状的复杂血管（主动脉血管和动脉分叉血管）模型、血管支架模型、血液模型，在主动脉血管、动脉分叉血管不同病变位置植入血管支架，建立血管-血液-支架的装配模型，导入Fluent进行流固耦合的动力学数值模拟，对不同情况下血管内压力大小、流速变化进行对比分析，将血液在流动过程在流固耦合面上产生的载荷加载到血管支架上，对其进行结构的有限元分析，校核其强度安全与否。

1 三维模型的建立

1.1 血管支架模型的建立

血管支架多分为圆形、矩形、三角形、菱形等，血管支架应该尽量顺应天然血管，并有良好的力学性能和生物相容性。本文根据血管的形状特征，利用Proe软件的环形弯折等命令建立了一种菱形结构血管支架，其内径为7.6 mm，外径为8.6 mm，如图1所示。

图1 血管支架模型

1.2 复杂血管模型的建立

人体内的复杂血管主要分为弯曲血管和分叉血管，前者以主动脉血管为代表，后者以动脉血管等为代表。

弯曲血管主要由升主动脉、主动脉弓和降主动脉组成。本文建立了如图2中的主动脉模型，其内径D为9 mm，血管壁厚t为2 mm，升主动脉长度L1为30 mm，降主动脉长度L2长度为60 mm，取内径与主动脉弓曲率直径d的比值λ为血管的管径曲率比，其中图2血管λ＝0.25，图3血管λ＝0.5.

在本文中为了研究血管的管径曲率比对植入血管支架后血液流动情况的影响，分别对图2和图3的血管模型进行数值模拟并分析；为了研究不同病变位置植入血管支架后，复杂血管内血液的流动情况的变化，分别在病变位置1和病变位置2植入血管支架，进行数值模拟并分析。

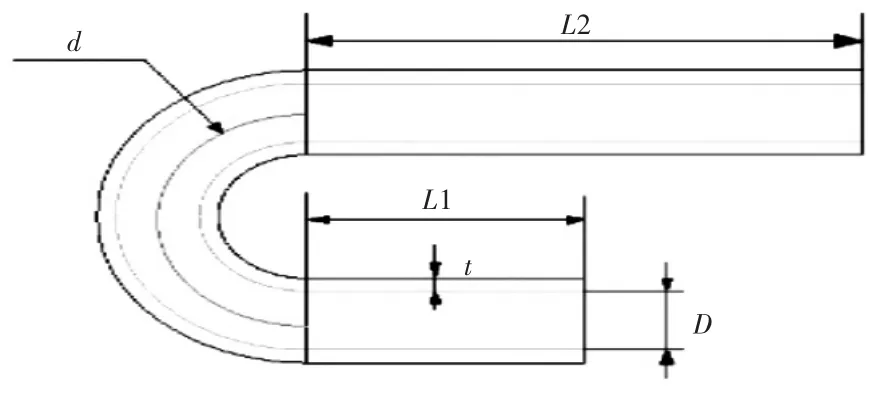
图2 管径曲率比为0.25的弯曲血管模型

图3 管径曲率比为0.5的弯曲血管模型

分叉血管主要由主动脉、外动脉和内动脉组成，其中内动脉上存在一个动脉窦，动脉窦是动脉粥样硬化疾病的多发区域[2]；分别建立如图4和图5中的模型，其主动脉内径D为9 mm，外主动脉内径D1为6.6 mm，内主动脉内径D2为6.6 mm，动脉窦内径D3为10 mm，血管壁厚t为2 mm，主动脉长度L1长度为60 mm，外动脉长度L2为40 mm，内动脉长度L3为60 mm，取 为内、外动脉之间夹角，如图4、图5所示。

图4 夹角为55°的分叉血管模型

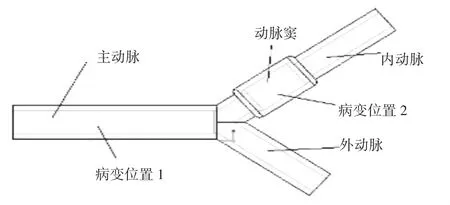
图5 夹角为75°的分叉血管模型

本文为了研究内、外动脉之间夹角对植入血管支架后血液流动情况情况的影响，分别对图4和图5的血管模型进行数值模拟并分析；为了研究不同病变位置植入血管支架后对血液流动情况情况的影响，分别在并病变位置1和病变位置2（动脉窦位置）植入血管支架，进行数值模拟并分析。

1.3 血管—血液—支架模型的建立

利用Proe软件分别建立血管、血液流域、支架的prt格式模型，并组装成asm格式的装配体模型，并利用Proe的切除功能，减去血液流域与支架相交的部分。分别建立对应不同管径曲率和病变位置的弯曲血管—血液—支架装配体模型，共4个，如图6、7、8、9所示，自上而下分别对应，血管支架位于病变位置1处；血管支架位于病变位置1处；血管支架位于病变位置2处；血管支架位于病变位置2处。

图6 弯曲血管—血液—支架装配体1

图7 弯曲血管—血液—支架装配体2

图8 弯曲血管—血液—支架装配体3

图9 弯曲血管—血液—支架装配体4

分别建立对应不同夹角和病变位置的分叉血管—血液—支架装配体模型，共4个，如图4所示，自上而下分别对应α＝55°，血管支架位于病变位置1处；α＝75°，血管支架位于病变位置1处；α＝55°，血管支架位于病变位置2处；α＝75°，支架位于病变位置2处。

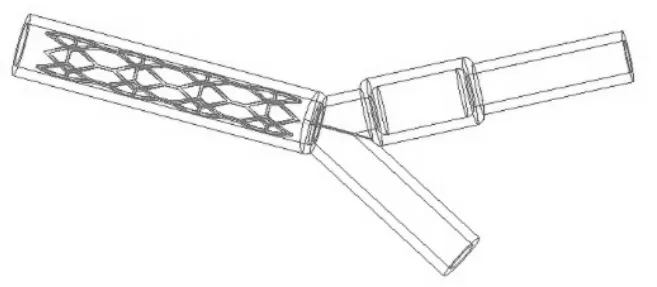
图10 分叉血管—血液—支架装配体1

图11 分叉血管—血液—支架装配体2

图12 分叉血管—血液—支架装配体3

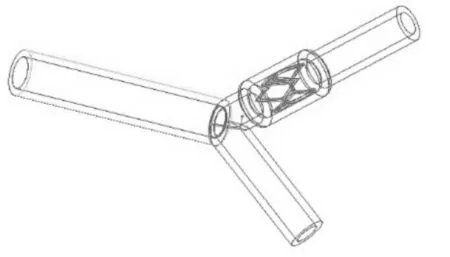
图13 分叉血管—血液—支架装配体4

2 动力学数值模拟及分析

打开 ANSYS workbench，分别建立 Geometry、Fluid Flow（Fluent）和 Static Structural模块，首先在Gometry模块导入装配体的x_t格式文件，然后建立如图5的工程，并建立相互之间的联系，实现数据的传递，如图14所示，将血管与血液流域间流固耦合面中的流体面命名为couple_flu_1，固体面命名为couple_wall_1；将血液流域与血管支架间流固耦合面中的流体面命名为couple_flu_2，固体面命名为couple_wall_2；确定血液流域的进口确定血管下底面为固定面，命名为fixed_1；确定血管支架底面为固定面，命名为fixed_2.依次建立上述8个模型的工程进行数值模拟。

图14 项目图

2.1 血液流域数值模拟及分析

进入Fluent，启动Energy方程，选择k-epsilon湍流模型，定义流体材料为blood，密度为1 090 kg/m3，粘度系数为0.003 5 kg/m-s；设置入口血液流速为0.14 m/s，温度为311.06 K，其中定义湍流强度为，式中，Re=1 000；水力直径为d=0.009 m，d=4=0.009 m；设置出口压力表压力为0，湍流强度和水力直径同上。忽略人体内环境，进行数值模拟，待数据收敛后查看结果，进行分析。

2.1.1 弯曲血管血液流域数值模拟及分析

当血管支架位于病变位置1，取血液流域中间平面进行分析。当管径曲率比λ=0.25时，管内血液压力在0 Pa-71.1 Pa之间变化，如图15压力云图所示，进口处压力全流域最大，为90.5 Pa，在升主动脉段，压力沿X轴负方向迅速降低，至46.2 Pa，其中未达到支架放置位置时，同一压力带向X轴正方向突出，管径中心处的压力较两侧血管支架所在处压力要小，此时血管壁受压力较大，当血液行至血管支架时，同一压力带向X轴负方向突出，管径中心处的压力较两侧血管支架所在处压力要大。在主动脉弓，压力带呈逆时针螺旋状分布，并逐次下降，从42.7 Pa降至17.8 Pa，但压力带分布密集，压力减小迅速，血液行至降主动脉时，压力在此沿X轴正方向逐渐下降，从17.8 Pa降至出口处为0 Pa.当管径曲率比λ=0.25时，血管内血液速度在2.99e-4 m/s-2.45e-1 m/s间变化，如图16速度矢量图所示，在升主动脉段，其中线处速度沿X轴负方向呈迅速增加，由1.4e-1 m/s-2.45e-1 m/s，之后保持稳定，两侧由于支架的存在流速较缓，处于至之间，当血液流经血管支架时，会形成小的漩涡。待血液行至主动脉弓，速度大小较上个阶段大幅降低并出现分层，主动脉弓左侧流速最快，在1.72e-1 m/s-2.08e-1 m/s之间，中线位置流速次之，在1.59e-1 m/s-1.72e-1 m/s之间，并一直延续到降主动脉段，右侧流速最慢，在1.23e-1 m/s-1.59e-1 m/s之间，并一直延续到降主动脉段。血液流至降主动脉，速度同样出现分层，中线速度开始大幅上升2.45e-1 m/s至并一直保持，两侧流速则较缓。

当管径曲率比λ=0.5时，管内血液压力在0 Pa-67.1 Pa之间变化，数值大小和变化范围较λ=0.25时都有所减小，如图17压力云图所示，血液行至主动脉弓，压力带同样呈逆时针螺旋状分布，并逐次下降，但压力带较图15密集，压力减小更快，对血管冲击较大，血液行至升主动脉段、降主动脉及血管支架时，除数值有所减小外，变化规律无显著不同。当管径曲率比λ=0.5时，管内血液速度在4.13e-4 m/s-2.36e-1 m/s变化，如图18速度矢量图所示，在升主动脉至主动脉弓中部，中线方向速度大小自入口处开始逐渐变大，由1.36e-1 m/s-2.01e-1 m/s，血液行至主动脉弓中部，其速度减小相对图16时较缓，随后在经主动脉弓下半段流至降主动脉后，流速除数值外无明显规律变化。

图15 当支架位于病变位置1时管径为0.25的弯曲血管压力云图

图16 当支架位于病变位置1时管径为0.25的弯曲血管速度云图

图17 当支架位于病变位置1时管径为0.5的弯曲血管压力云图

图18 当支架位于病变位置1时管径为0.5的弯曲血管速度云图

当血管支架位于病变位置2，取血液流域中间平面进行分析。当管径曲率比λ=0.25时，管内血液压力在-6.50 Pa-90.5 Pa之间变化，如图19压力云图所示，进口处压力最大为90.5 Pa，在升主动脉段，压力沿X轴负方向呈线性降低至75.9 Pa，待血液行至主动脉弓，压力带呈逆时针螺旋状分布，并逐次下降，从71.1 Pa降至46.8 Pa，但压力带分布较疏，压力减小相对图15血管支架位于病变位置1时的情况较慢，对血管压迫较小，血液行至降主动脉时，压力在此呈现性下降，至出口处为-6.50 Pa，在血液行至血管支架时，同一压力带向X轴正方向突出，管径中心处的压力较两侧血管支架所在处压力要大。当管径曲率比λ=0.25时，管内血液速度在1.52e-4 m/s至2.32e-1 m/s变化，如图20速度矢量图所示，在升主动脉段，速度方向沿X轴负方向，其大小在1.39e-1 m/s-1.51e-1 m/s之间，其两侧边缘流速较大，为1.51e-1 m/s-1.63e-1 m/s之间，待血液行至主动脉弓，速度大小出现明显变化，并分为3个层次，主动脉弓左侧流速较慢，在1.16e-1 m/s-1.39e-1 m/s之间，沿中线处流速较快，在1.51e-1 m/s-1.63e-1 m/s之间，右侧流速最快，在1.74e-1m/s-2.09e-1 m/s之间，血液行至降主动脉时，速度出现整体增大，中线处流速普遍处于1.98e-1 m/s-2.32e-1 m/s之间，两侧由于支架的存在流速较缓，处于1.28e-1 m/s-1.63e-1 m/s之间，当血液流经血管支架时，会形成小的漩涡。其温度云图无明显变化，这里不再举出。当管径曲率比λ=0.5时，管内血液压力在-5.36 Pa-72.2 Pa之间变化，数值大小和变化范围较λ=0.25时都有所减小，如图21压力云图所示，血液行至主动脉弓，压力带同样呈逆时针螺旋状分布，并逐次下降，但压力带较密集，压力减小快速，对血管冲击大，血液行至升主动脉段、降主动脉及血管支架时，除数值有所减小外，变化规律无显著不同。当管径曲率比λ=0.5时，管内血液速度在1.74e-1 m/s-2.47e-1 m/s变化，如图21速度矢量图所示，在升主动脉至主动脉弓中部，中线方向速度大小自入口处开始逐渐变大，由1.36e-1 m/s-2.22e-1 m/s，其两侧流速较缓，随后在主动脉弓下半段流速变缓慢，但进入降主动脉后，流速迅速攀升至2.10e-1 m/s-2.47e-1 m/s间，其余流动规律较λ=0.25时，除数值大小外无明显变化。

图19 弯曲血管病变位置2仿真结果

图20 弯曲血管病变位置2仿真结果

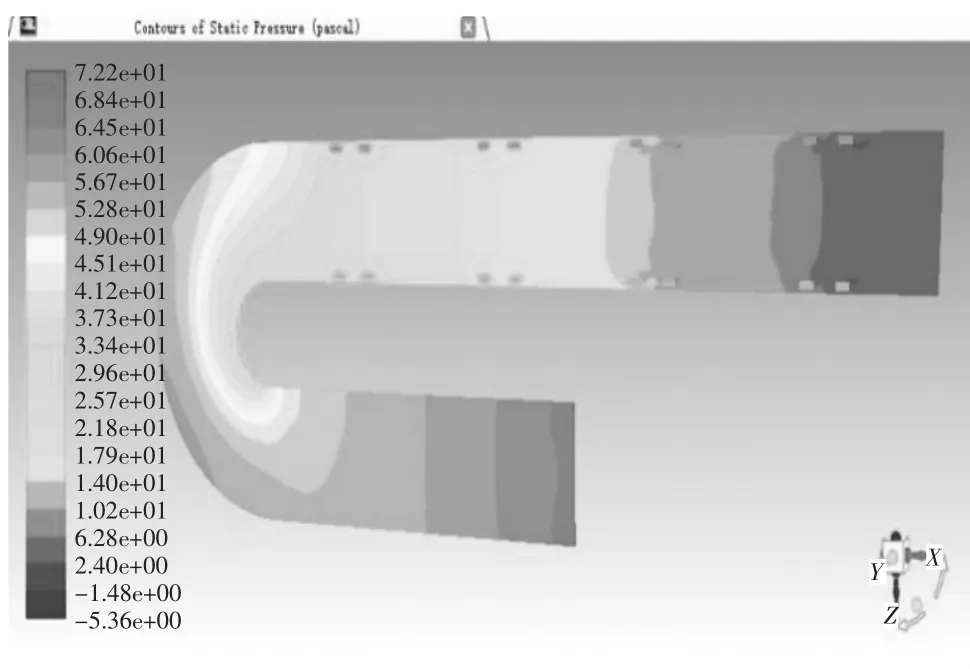
图21 弯曲血管病变位置2仿真结果

图22 弯曲血管病变位置2仿真结果

2.1.2 分叉血管血液流域数值模拟及分析

当血管支架位于病变位置1，取血液流域中间平面进行分析。当夹角α＝55°时，管内血液压力在-13.62 Pa-85.25 Pa之间变化，如图23压力云图所示，进口处压力最大为85.25 Pa，在主动脉段，压力沿Y轴负方向呈线性降低至22.81 Pa，在血液行至血管支架时，同一压力带向Y轴负方向突出，管径中心处的压力较两侧血管支架所在处压力要大，待血液行至主动脉与内、外动脉的接口处和内、外动脉分叉时，压力发生较为密集的波动，随后平稳在22.81 Pa-28.01 Pa间，内动脉血液在进入动脉窦压力逐渐降低，由17.6 Pa降至出口处的13.62 Pa，外动脉血液同样如此。当夹角时α＝55°，管内血液速度在2.08e-4 m/s-2.88e-1 m/s间变化，如图24速度矢量图所示，在主动脉段，血液速度方向沿Y轴负方向变化，其大小在1.4e-1 m/s-2.32e-1 m/s之间，沿中线流速较大，为2.08e-1 m/s-2.32e-1 m/s之间，两侧流速较缓，在流经血管支架所在位置时，会发生小的漩涡，待血液行至主动脉与内、外动脉的接口处时，流速突然增大至2.16e-4 m/s-2.88e-1 m/s间，随后降低，内、外动脉的接口处两侧会发生明显的漩涡，内动脉内的血液在流经动脉窦时会迅速降低2.08e-4 m/s-8.64e-2 m/s间，并在动脉窦外壁上形成明显的漩涡，流出动脉窦后，流速升高至1.44e-1 m/s-2.01e-1 m/s间，之后的流域中，内动脉内的血液流速一直稳定在到间，直至出口。当夹角α＝75°时，管内血液压力在-15.46 Pa-86.07 Pa之间变化，如图25压力云图所示，较之夹角α＝55°时压力变化不大。当夹角α＝75°时，管内流速速度在5.19e-4 m/s-2.97e-1 m/s间变化，如图26速度矢量图所示，内外动脉接口处流速变化较夹角α＝55°时小，其在经过动脉窦时流速较夹角α＝55°时小，在内、外动脉出口处流速也有所减低，其余流动规律除数值大小外无明显变化。

图23 分叉血管病变位置1仿真结果

图24 分叉血管病变位置1仿真结果

图25 分叉血管病变位置1仿真结果

图26 分叉血管病变位置1仿真结果

当血管支架位于病变位置2，取血液流域中间平面进行分析。当夹角α＝55°时，管内血液压力在-15.6 Pa-71.55 Pa之间变化，如图27压力云图所示，压力变化范围和数值大小较支架位于病变位置1时有所减小，在主动脉段，压力沿Y轴负方向呈线性降低，同一压力带界面压力无明显不同，待血液行至主动脉与内、外动脉的接口处和内、外动脉分叉时，压力波动较为较缓，在血液行至动脉窦时，其压力平稳在27.97 Pa-36.69 Pa间，压力数值大小较支架位于病变位置1时明显增大。当夹角α＝55°时，管内血液速度在1.13e-4 m/s-2.89e-1 m/s间变化，如图28速度矢量图所示，在主动脉段，血液速度方向沿Y轴负方向，流速较大，且管径两侧产生的漩涡较少较小，在流经动脉窦血管支架所在位置时，动脉窦内侧与血管支架位置产生漩涡明显增多。当夹角α＝75°时，管内血液压力在-16.84 Pa-70.03 Pa之间变化，如图29压力云图所示，在主动脉段，压力沿Y轴负方向呈线性降低，同一压力带界面压力无明显不同，待血液行至主动脉与内、外动脉的接口处和内、外动脉分叉时，压力带分布较α＝55°时更为密集，压力变化较剧烈，对血管冲击较大，在血液行至动脉窦时，其压力平稳在28.88 Pa-38.02 Pa间。当夹角α＝75°时，管内血液速度在9.95e-5 m/s-2.92e-1 m/s间变化，如图30速度矢量图所示，在主动脉段，血液速度较α＝55°时变化不大，待血液行至主动脉与内、外动脉的接口处和内、外动脉分叉时，速度较α＝55°时有明显减小，在流经动脉窦血管支架所在位置时，动脉窦内侧与血管支架位置产生漩涡明显增多。

图27 分叉血管病变位置2仿真结果

图28 分叉血管病变位置2仿真结果

图29 分叉血管病变位置2仿真结果

图30 分叉血管病变位置2仿真结果

2.2 血管支架的有限元分析

对血管支架划分网格，其材料为钛镍合金，定义材料属性，密度为6 300 kg/m3，弹性模量为193 GPa泊松比为0.3，在人体温度时屈服强度为230 MPa，设置fixed_2为血管支架固定面，将血液与血管之间流固耦合面上受到的载荷加载到血管支架上，如图31所示，进行有限元分析，如图32所示为血管支架变形情况，如图33所示为血管支架等效应变分布，如图34所示为血管支架等效应力分布。对于植入弯曲血管的血管支架，具体分析结果如表1所示，对于植入分叉血管的血管支架，具体分析结果如表2所示。

图31 血管支架上受到的载荷

图32 血管支架的变形

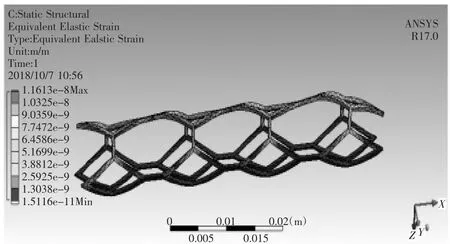
图33 血管支架的等效应变分布

图34 血管支架的等效应力分布

因为在人体温度时，钛镍合金屈服强度为230 MPa，所有在上述所有情况下的血管支架均较核安全[5]。

3 结论

本文建立了菱形血管支架、两种不同复杂血管以及血液的三维模型，并进行装配。在不同形状血管的两处病变位置各植入血管支架，创建了8个工程，进行数值模拟，并对所有情况下血管内血液的压力与流速情况进行分析比较，得到在弯曲血管病变位置1和病变位置2植入血管支架时，不同管径曲率比对于管内压力分布和流速情况的影响；得到在分叉血管病变位置1和病变位置2植入血管支架时，不同夹角对于管内压力分布和流速情况的影响。在上述血液动力学的仿真、分析的研究基础上，运用流固耦合的技术，将血流对于血管支架作用作为载荷施加到血管支架上，对其进行结构的有限元分析，仿真结果表明在各种情况下，血管支架的强度均校核安全。

表1 弯曲血管内血管支架分析情况

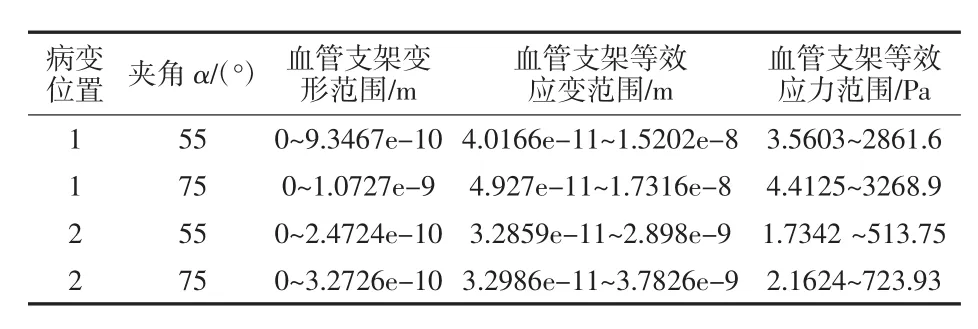
表2 分叉血管内血管支架分析情况