基于EMD的小波神经网络模型预测大坝变形

王玉振

(河南水利与环境职业学院，河南郑州450008)

及时获取大坝变形的演变规律并作出准确预报，对大坝安全具有重要意义[1]。由于大坝变形受温度、水压和时间效应等诸多因素影响，呈现出高度的非线性和非平稳性，难以建立较为准确的变形量与影响因素之间复杂的关系模型，因此，预测效果不佳[2]。目前，继BP(Back Propagation，BP)神经网络之后的小波神经网络(Wavelet Neural Ntworks，WNN)模型被广泛用于非线性、非平稳性时间序列预测，其结合了小波变换和人工神经网络各自的特点，具备极强的自学习能力和小波变换局部化等优点[3]，能够有效解决局部极小值问题。但在实际应用中发现，其存在小波分解无法实现的自适应多分辨率分析问题[4-5]。而经验模态分解法[6-7](Empirical Mode Decomposition，EMD)在信号处理和分析中具有自适应的良好特性，能够有效弥补小波神经网络自适应多分辨率分析的不足。本文考虑影响因素对大坝变形的影响，并采用组合模型的思想，将经验模态分解法和小波神经网络相结合，充分发挥两者各自的优势，将有望对大坝变形中隐含的特征信息进行多层次、多角度挖掘和分析，从而提高预测精度。

1 基于EMD的小波神经网络预测模型

1.1 经验模态分解原理

EMD是N.E.Huang等人提出的一种信号分解技术，无须预先设定基函数，就可以自适应地将非平稳、非线性时间序列中的的波动和趋势分离开，形成若干个固有模态分量IMF和1个余项，其实质是平稳化数据处理。对于任意一变形时间序列S(t)，对其进行经验模态分解，步骤参照文献[8]。因此，原始序列可以表示为

(1)

式中，S(t)为原始数据监测信号；t=1，2，3，…，m为时间采样序列，其中，m为采样总次数；IMFi为分解所得的第i个IMF分量；i=1，2，3，…，n为IMF分量的次序，是按频率由高到低依次排列；B为单调残余函数(EMD分解后的趋势分量)。

1.2 游程判定法重构原理

1.3 预测模型及流程

大坝变形的影响因素分为水位、温度、时效三部分，设大坝在不同时间段的变形序列为{Y(x)=(tx，Hx，Tx)，x=1，2，…，n}，其中，t为时效量；H为上游水位影响因子；T为温度影响因子。经EMD对大坝变形原始数据Y分解得到n个IMF和一个剩余量B，然后通过游程判定法对各分量进行重构得到高频项F1、中频项F2和低频项F3，设对应的预测值分别为E1、E2和E3，模型预测流程如图1所示，则最终的预测值

G=E1+E2+E3

(2)

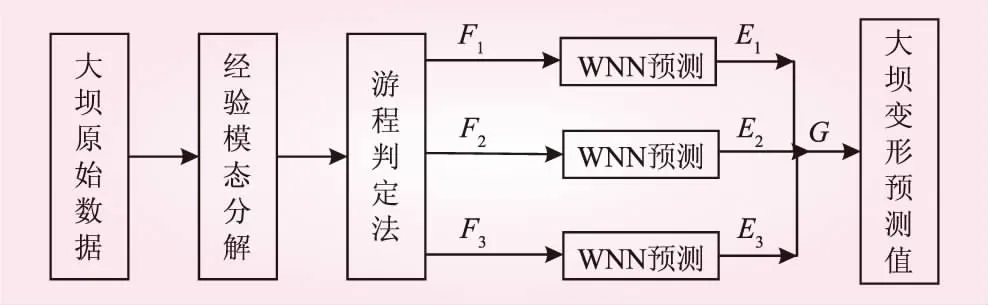
图1 模型预测流程

1.4 模型精度评定

为了评价各模型预测性能的优劣，本文采用均方根误差(Root Mean Square Error，RMSE)和平均绝对误差(Mean Absolute Error，MAE)作为模型评价指标。

平均绝对值误差(MAE)

(3)

均方根误差(RMSE)

(4)

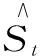
2 算例

2.1 实验数据获取及分析

本文以丰满大坝30号坝段1985年1月4日～1987年6月22日的坝顶水平位移及同期库水位、温度和时效的实测资料为例[10]，共140期观测数据，建立模型进行分析，如图2所示。

图2 大坝变形水平位移序列

由图2可见，该大坝变形较剧烈，无明显规律可循，若直接建立模型进行预测分析，很难得到可靠的结果。本文先采用EMD对其进行预处理，分解结果见图3。

图3 EMD分解结果

由图3可知，EMD将变形序列自适应分解为4个IMF和一个残余分量B，使各分量变化曲线比原来变形曲线(图2)更光滑和平稳。EMD可以降低其非平稳性，将相同和类似信息独立出来，有利于模型的建立和分析。但经EMD分解得到的分量个数多，会增加建模次数。因此，有必要采用游程判定法对各分量进行波动程度分析。IMF1、IMF2、IMF3、IMF4、B的游程总数分别为66、15、7、3、2。

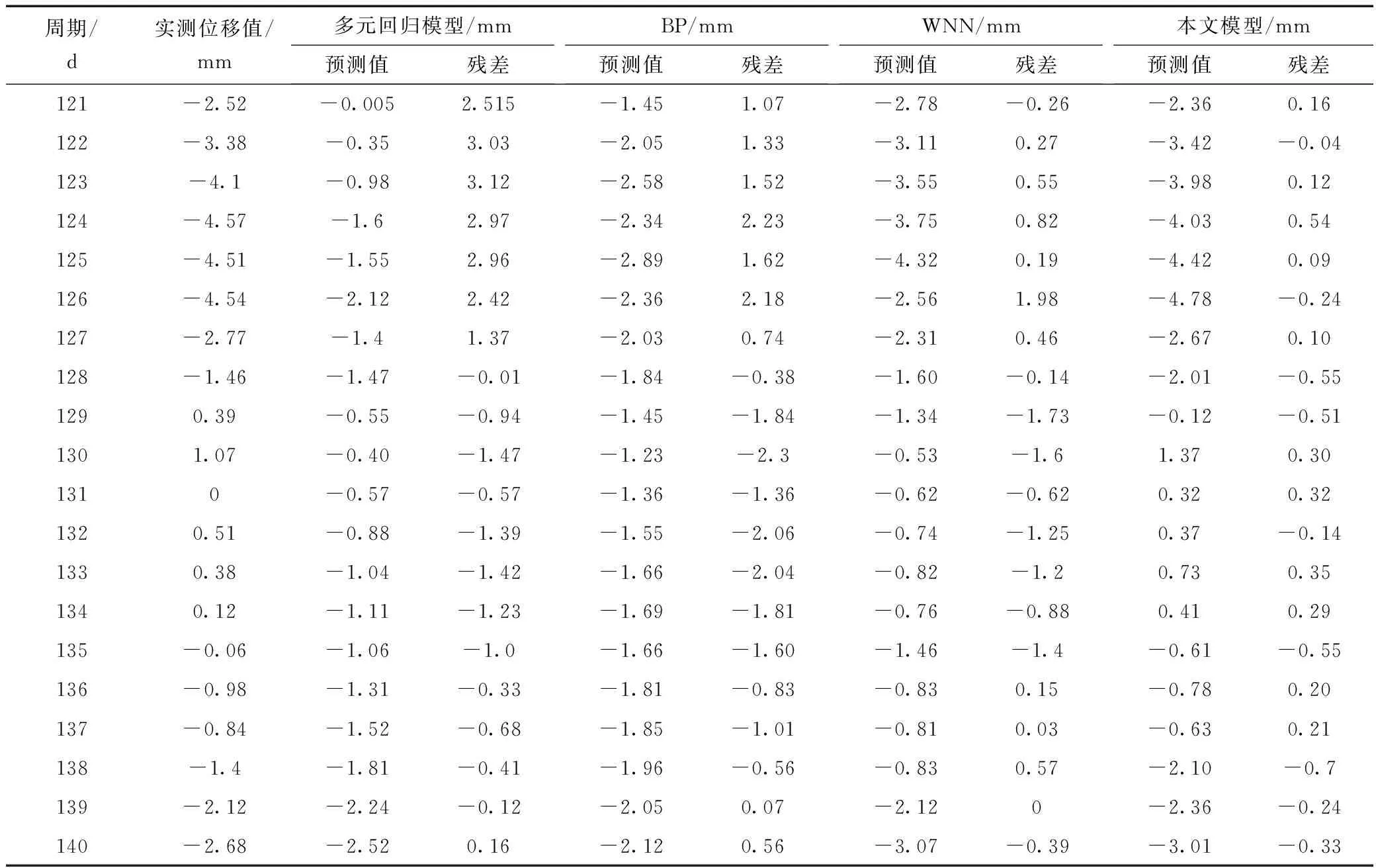
表1 各模型预测结果与实际值对比

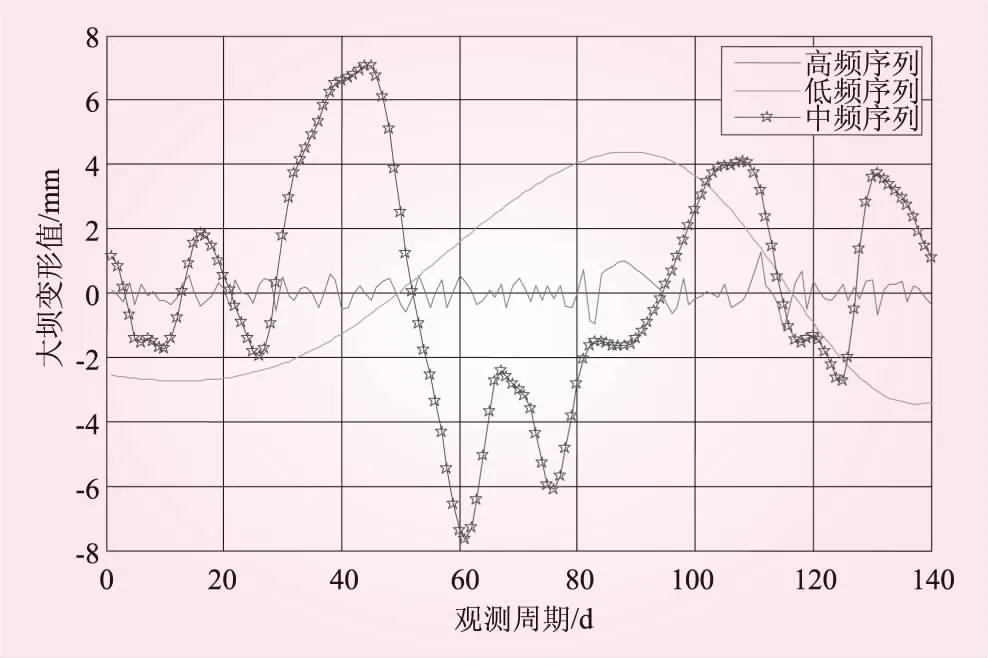
图4 重构结果

由于游程总数反映出各分量的波动程度，所以将IMF1作为高频分量，IMF2和IMF3叠加作为中频分量，IMF4和余量B作为低频分量。重构结果如图4所示。

经重构后，可以减少建模次数和简化数据处理过程，提高预测效率。为验证本文算法的可行性和有效性，建立4种方案进行对比分析：①方案1。多元回归模型。②方案2。BP神经网络模型。③方案3。WNN模型。④方案4。基于EMD的小波神经网络大坝变形预测模型。

2.2 预测结果对比分析

本文分别利用WNN训练和测试经EMD分解重构后的高、中和低频分量，并叠加各个预测值即为最终大坝变形预测结果，各模型预测结果见表1。

由表1可知，本文模型求出的残差较小，最大残差为0.7 mm，最小只有0.04 mm，其余残差都小于1 mm，而其他模型的残差均有大于1 mm的情况，不能保证较好的全局预测精度。因此，本文模型能较好地表达大坝变形分量与其影响因素之间复杂的关系，预测值与实际值吻合最好，均优于其他模型，预测精度较高。为了更直观地探讨各模型的预测效果，将各模型的预测值与大坝变形的真实值进行对比分析，见图5。

图5 各模型预测结果与实际对比

由图5知，方案1、2和3预测不稳定，部分预测值与实际值相比偏差较大，尤其在变形幅度较大的第121到127期、129到135期，波动比较大。而方案4的预测值与实际值吻合最好，表明基于EMD的小波神经网络预测模型能较好地反映大坝变形规律，说明EMD能自适应地分析和提取变形时间序列中隐含的特征信息，将相同或类似的信息独立出来，使得模型的自身性得到充分发挥，有效地弥补了小波神经网络无法实现自适应多分辨率分析的不足，取得了较好的效果。同时，采用游程判定法将相同或相似波动程度的信息重新组合，减少了建模次数，提高了预测效率。为了进一步探讨各模型的预测效果，各模型预测精度见表2。

由表2可看出，多元回归、BP和WNN模型精度指标较差，不能很好地表达大坝变形与其影响因素之间复杂的函数关系。而本文利用EMD对大坝变形原始数据进行分解，能有效挖掘其内部规律，建立影响因素与变形分量之间复杂的关系模型，预测精度均优于WNN、BP和多元回归模型，具有较好的泛化能力，可信度较高。这是由于EMD与WNN的结合，充分发挥了两者各自的优势，提高了预测精度。综上，说明有必要先对非线性、非平稳时间序列进行EMD分析，这为大坝变形预测研究提供了一种新思路。

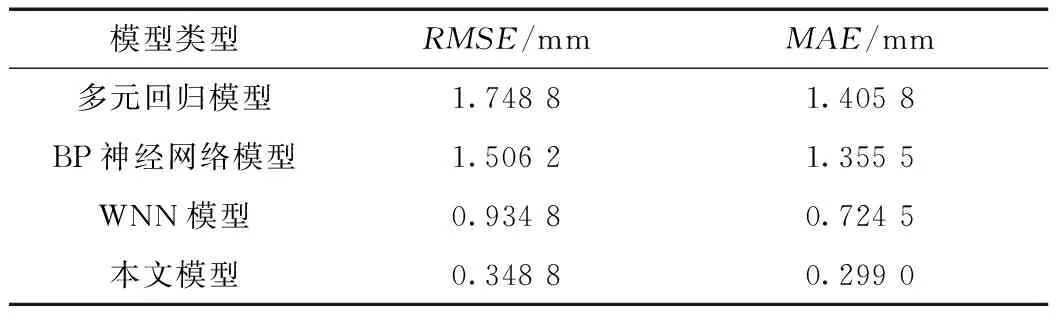
表2 各模型精度对比

3 结 语

目前，WNN是时间序列预测方法中较为理想的一种预测方法，但是其具有在预测中无法实现自适应多分辨率分析的不足，而利用EMD可以解决此问题。本文提出一种基于EMD的小波神经网络大坝变形预测模型，经理论和算例分析，并与多元回归、BP神经网络和WNN模型对比分析表明，该算法预测精度较高，可以用于大坝变形预测。