用爱因斯坦固体模型理解熵的微观含义

柳潇凡

熵在物理学中是一个非常重要的概念。通过对熵的深入了解，我们对于热力学中物质的演化过程将更加清楚。并且随着科技的进步，熵这一原本局限于实验室的概念，也流传到了我们的日常生活中，熵这一名词已经进入了环保、经济、工业等诸多行业。为了更好地了解熵的概念，本文介绍了熵的宏观定义与微观定义，然后在爱因斯坦固体模型中具体计算相关的熵情况，同时介绍了熵的微观与宏观定义的等价性。

1 熵的定义

1.1 克劳修斯关于熵的宏观定义

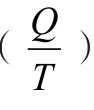
若考虑工作物质吸收的能量为正，放出能量为负，则上述式子可改写为：

由此在工作物质经历1次循环中，比热容的代数和为零，也可以证明出：

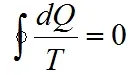
因此在图2由A→B→A的过程中，

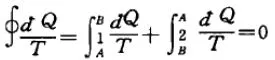
由此可得：

通过上式即可发现，当其初末态确定时比热容的代数和唯一确定与过程无关。这一状态函数被克劳修斯定义为熵，用S表示。

图1

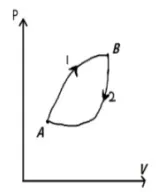
图2

1.2 玻尔兹曼关于熵的微观定义

20年后，玻尔兹曼从统计力学的角度对熵进行了微观定义，在任意的宏观状态下，熵与该宏观状态下的微观状态数的自然对数成正比。后来普朗克将这个关系写为：

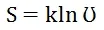
2 爱因斯坦固体模型与相关熵的定量计算

由于能够简单算出微观状态数的状态模型极少，此处我只分析爱因斯坦提出用于描述简单晶体热学性质的固体模型。该模型可等效成1个由相同的量子谐振子组成的系统，每个粒子有3个自由度，每个自由度上都可以看作是1个谐振子，这样每个粒子就等效于成3个自由谐振子。而每个谐振子的能量是量子化的，并且其能量是相对于基态能量的某个能量单位的整数倍。通过了解爱因斯坦固体的微观状态数，可以简单计算相应的熵值。

我们不妨假设下述的1个爱因斯坦固体，其振子数为3，系统总能量U为4，当其总能量为4时，其能量分配方式共有15种，分别为（4,0,0），（3,1,0），（3,0,1），（2,2,0），（2,1,1），（2,0,2），（1,3,0），（1,2,1），（1,1,2），（1,0,3），（0,4,0），（0,3,1），（0,2,2），（0,1,3），（0,0,4）。当其总能量为3时，其能量分配方式共有10种，分别为（3,0,0），（2,1,0），（2,0,1），（1,2,0），（1,1,1），（1,0,2），（0,3,0），（0,2,1），（0,1,2），（0,0,3）。当其总能量为2时，其能量分配共有6种，分别为（2,0,0），（1,1,0），（1,0,1），（0,2,0），（0,1,1），（0,0,2）。当其总能量为1时，其能量分配共有3种，分别为（1,0,0），（0,1,0），（0,0,1）。当其总能量为0时，其能量分配有1种，为（0,0,0）。

观察上述数据，不难得出规律N个谐振子的爱因斯坦固体，在总能量为U的情况下，其微观状态数为：

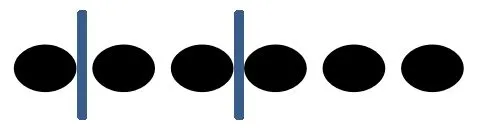
我们可以换个角度看待该式，将量子化的1份能量看作1个小球，并使用1条竖线来分隔2个谐振子，则问题转化为在小球间插入2块隔板，使小球分为3份。

通过以上我知道了一个孤立的爱因斯坦固体的微观状态数，为了更加透彻地理解相互作用系统的熵值变化，再来看2个爱因斯坦固体的情况，设有A、B的2个爱因斯坦固体，初始能量为U1、U2，含有N1、N2个振子，则系统总能量为U= U1+ U2,而U在能量交换过程中不变。又因为，A、B的2个固体之间只存在比较弱的相互作用，所以可以将它们看成相对独立的2个固体，故。现假设在2个爱因斯坦固体组成的系统中，N1=N2=3，U=U1+U2=9，则可得到表1的数据。

表1

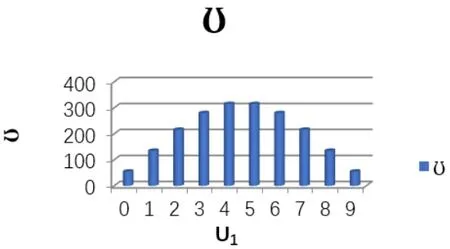
图3

而当N1=N2=100，U=U1+U2=120时，又有图4。

图4

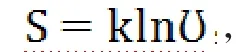
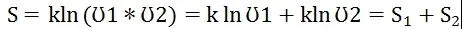
3 关于熵的2种描述的一致性

S与S1、S2的关系如图5所示（其中横坐标代表U1）。

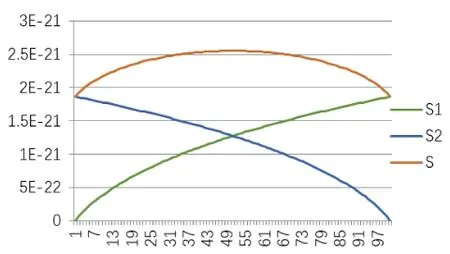
图5

由图像可知，当S1曲线与S2曲线斜率的绝对值相同时，S曲线取到峰值，此时对应的微观状态数最多，处于最可能的宏观状态，且基本不再有能量流动。

此时满足函数关系

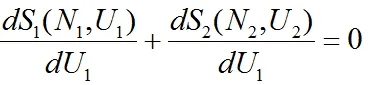
又∵ U=U1+U2

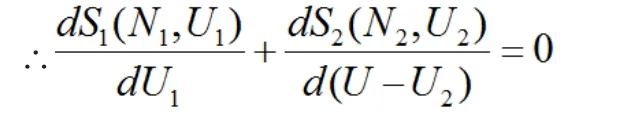
又∵U为常数

由此我们也可以看出熵的宏观与微观定义的一致性。根据热力学第一定律,而此处体积不变，可将做功部分看作为零，故，根据克劳修斯的熵的定义，，而根据玻尔兹曼的定义，上式仍成立，这极好的验证了熵的宏观、微观定义的一致性。

4 结语

虽然19世纪发现的热力学第一定律作为物理科学的重大发现之一，并备受推崇，但是对于热力学第二定律，人们的重视程度却一直不够。然而，在20世纪，熵理论的应用远远超出了经典热力学的范畴。它不仅在非生物界，而且在生物界以及经济学、社会学等学科的研究和应用中都显现出广阔的发展前景,因此,进一步对熵的研究很有必要。从克劳修斯的宏观定义中，我了解到熵作为自发过程进行方向的标志，在系统自发演化的过程中，总是满足熵增原理。在爱因斯坦固体中，可以清楚地看到系统的熵与系统的微观状态数有着密切的联系，孤立的与外界没有相互作用的系统，总是从微观状态数少的熵较小的状态变化到微观状态数大的熵较大的状态，而不会从熵大的状态向熵小的状态去变化发展。