基于功率增量变化百分比的变步长功率追踪方法研究

李 昱，黄汉生，巫 卿，王 瑾，杨 阳，俞 雷，胡 琴

（1．中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳550000；2．广东电网有限责任公司肇庆供电局，广东 肇庆526040）

0 引 言

太阳能是一种极为丰富的可再生能源，光伏发电则是收集太阳能的主要方式。而光伏发电输出功率受光照强度、环境温度和输出电压共同影响，某一时刻只存在一个最大功率点（Maximum Power Point，MPP），因此如何快速和准确地找到该功率最大点对提升光伏发电输出效率至关重要［1］。

当前，定时（电压或电流）扫描法虽能准确定位功率最大点，但计算时间长；定（电压或电流）填充系数法较为简单，但输出功率不连续，只能得到MPP的近似值；扰动观察法的计算精度和速度取决于初始值和跟踪步长的大小；电导增量法，该法中｜dP／dU｜＝ε的阀值过大时会造成精度不足，过小时将产生振荡的问题［3］。

本文在传统扰动观察法基础上，提出一种基于功率增量变化百分比为控制因素的变步长功率追踪方法。

1 光伏电池模型及主要输出特性

光伏电池模型如图1所示。其中Iph为光伏电池生成电流；Rj为PN结阻抗（非线性），Dj为PN结二极管，Rsh和Rs可忽略不计，Ro是负荷电阻，I为光伏电池的输出电流，U为光伏电池的输出电压。

针对图1所示的光伏电池模型，其输出特性为：和电流，表达式为：

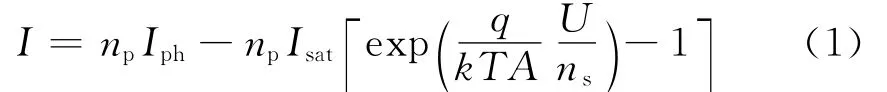
式中，np为光伏电池模块的并联数量；ns为光伏电池模块的串联数量；q为电荷量（×10－19C）；k是波尔兹曼常数（1．38×10－23J／K）；T 为温度（光伏电池绝对温度）；A是光伏电池理想因数（A＝1～5）；Isat为反向饱

式中，Tr为光伏电池参考温度；Irr为光伏电池温度为Tr时所产生的反向饱和电流；而EGap为半导体材料在跨越能带间隙时所需要吸收的能量（硅的EGap≈1．1 eV）。光伏电池所产生电流Iph的大小，由太阳照度和大气温度两个因素决定：

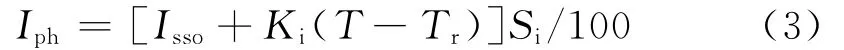
式中，Isso为光伏电池在参考温度和日照条件（100 MW／cm2）下所测得的短路电流值，Ki表示短路电流温度系数，Si为日照强度（MW／cm2）。则其输出功率P：

由以上式子可得到光伏发电P－U、U－I特性曲线，进而获得MPP。

图1 光伏电池模型

2 基于功率增量变化百分比的变步长功率追踪方法

在传统扰动观察法中，反复扰动和判断就有可能导致在最大功率左右不停的振荡，而运用电导增量法又存在阈值过小，在一定范围内会发生振荡［4］。因此可综合以上两方面影响，将功率增量变化百分比｜Pk－Pk－1｜÷（｜Pk－Pk－1｜＋λ）作为控制变量，其中λ为控制最大功率追踪速度因子（λ＞0）。可以看出，变步长功率追踪法随着与最大功率点的距离越近，所取步长越小；反之，与最大功率点的距离越远，所取步长越大。当｜dp／dU｜＜ε（ε为功率追踪要求的精度）时，功率追踪结束。由于存在步长随着功率增量变化这一机制，因此可以保证功率追踪一直向MPP点快速而又稳定的靠近，在满足精度要求下，功率追踪即可结束。

取功率追踪始发点为U0＝Uoc×0．8，初始步长为5%Uoc，｜dp／dU｜→0时追踪结束，改进步长流程图如图2表示。

图2 变步长功率追踪流程图

3 基于STP180s－24／Ac型太阳能组件的算例分析

为验证基于功率增量变化百分比的变步长功率追踪方法的准确性，以无锡尚德公司生产的STP180s－24／Ac型太阳能组件作为研究对象进行仿真实验，其技术参数如表1所示。

表1 STP180s－24／Ac型太阳能电池板技术参数

基于式（1）～式（4），采用 Matlab／Simulink仿真软件建立了该电池的数学模型，其光伏阵列特性曲线如图3所示。

图3 电池特性曲线

在仿真中设置环境温度为25℃。采用传统扰动观察法，设置固定仿真步长为0．01 s和0．5 s，运行时间为6 s。光照强度由600 W／m2上升到1 000 W／m2，仿真结果分别如图4所示。运用基于功率增量变化百分比的变步长功率追踪方法，控制速度因子λ＝2，控制精度为ε＝0．001，得到的仿真波形如图5所示。

图4 固定步长仿真波形

图5 变步长仿真波形

由以上两图可以看出：固定步长时，若步长较大，则追踪速度比步长小时快0．3 s，追踪过程中稳定性较好，但在最大点出现±1 W的振荡；若步长较小，则追踪速度较慢，追踪过程中稳定性较差，但达到稳定后只出现±0．5 W的振荡。而变步长时，不仅追踪速度快（几乎为0s），追踪过程中稳定性较好，而且达到稳定后振荡的幅度只有±0．3 W。

4 结 论

本文在传统扰动观察法的基础上，提出了以功率增量变化百分比为控制变量的功率追踪方法。该方法速度快，几乎为0s就可以响应，而且震荡幅值低，只有±0．3 W。