含有L1数据保真项的非凸优化脉冲噪声去除模型①

陈静思,李 春

1(云南财经大学 云南省经济社会大数据研究院,昆明 650221)

2(中国科学院大学,北京 100049)

3(中国科学院 计算机网络信息中心,北京 100190)

在计算机视觉与图像处理工作中,图像恢复是该领域的一个重要问题之一,在过去的几十年里,该问题得到了广泛的研究[1–7].在现实生活中,由于数字图像含有丰富的科学信息,所以图像处理已经被应用到人类生活的方方面面.例如: 在医学领域,通过图像处理技术,研究人员可以通过图像去燥算法把一幅受噪声污染或者信息缺失的图像从中恢复出来,从而提供清晰的图像帮助医生做出准确地医学诊断,从而实现实际意义的“精准医疗”.在自然保护区领域,研究学者可以通过对相关保护区域遥感图像的分析,进行濒危物种的保护,从而帮助自然保护工作者做出精准决策.在气象农业领域,通过对遥感图像进行去燥处理,从而可以对其进行图像分析,可以对土地覆盖分类、植被分布、病虫害防治等做出辅助决策.在现实生活的图像处理技术中,图像的质量是任何研究的重点,图像去燥就是提高图像质量的重要环节.

1 图像恢复概述

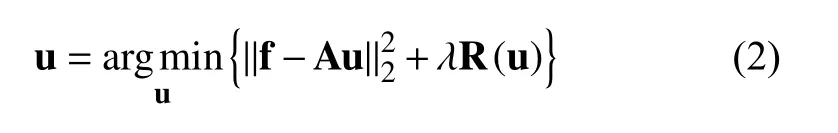
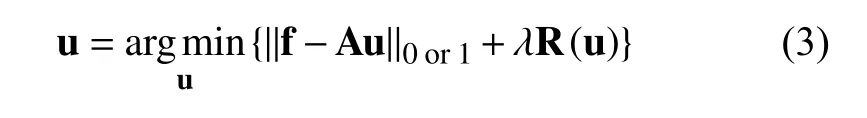
著名的正则方法是变分正则[8],其中凸变分正则要求该模型算法解存在并且唯一.在最近几年中,人们为了得到恢复后的图像能保持更多的图像细节信息,从而相关学者尝试应用非凸非光滑优化正则方法,来保持图像的细节信息.例如: 在变分框架和统计学习框架中,相关学者引入了非凸非光滑优化[9,10],如文献[11,12]对该现象给出了数值例子,文献[13]对该现象给出了理论解释.

在过去的几十年中,相关学者对非凸非光滑优化正则方法,提出了许多数值解法,如最小二次方重权迭代法[11],半二次算法[14]等.在本文中,我们利用非凸非光滑优化来对脉冲噪声进行去除处理.为了处理非凸非光滑性,本文采用了多阶凸松弛方法对模型进行求解[15],从其数值例子可以看出,其近似解比标准的L1凸或者L1凸松弛方法的逼近解好了许多,虽然该方法仅导致原始非凸问题的局部最优解,但该局部解是对初始凸松弛的全局解的改进.此外,因为每个阶段都是凸优化问题,所以该方法在计算上是高效的.

2 相关工作

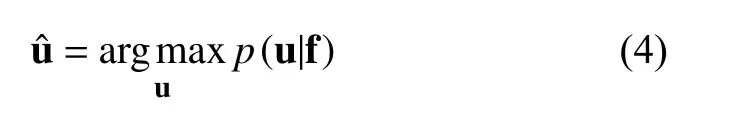
利用贝叶斯法则,可以得到如下表达式:

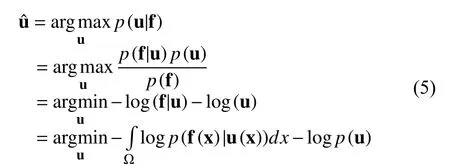
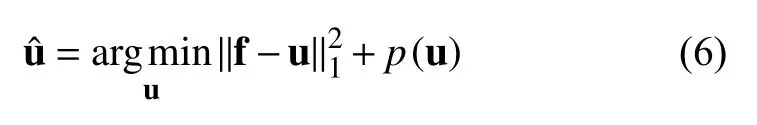
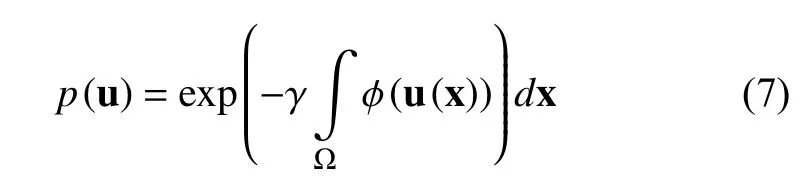
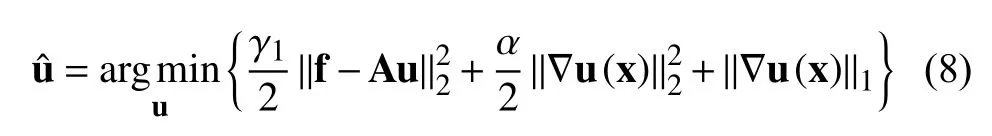
由于L1-范数能很好的拟合脉冲信号,所以为了有效的去除脉冲信号,L1数据保真项在如下的文章中被广泛使用[19–21],例如: 基于 TVL1模型,相关学者提出了如下的脉冲信号去除模型STVL1 (Squares TVL1):

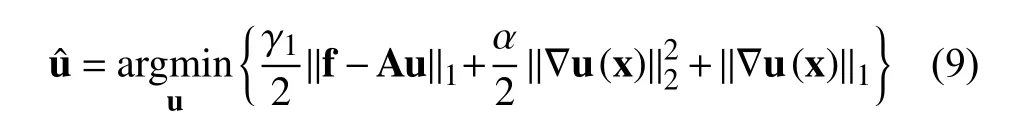
为了去除混合噪声,Shi[7]联合了式(8)、(9)提出了如下的去燥模型:

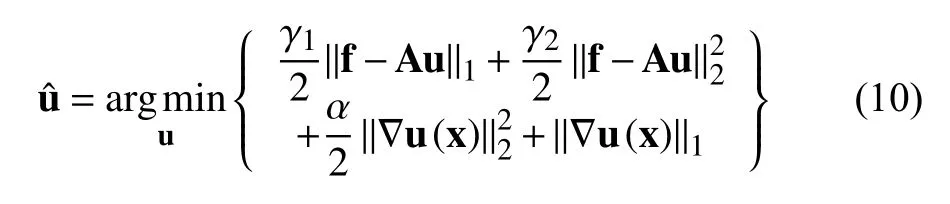
但是,这些模型虽然能去除脉冲噪声,但是还有很大的提升空间,所以我们基于以上的几个模型,提出了如下的脉冲噪声去除模型:

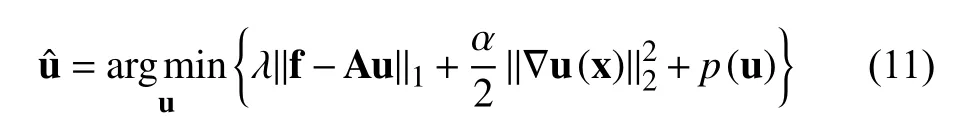
其中,

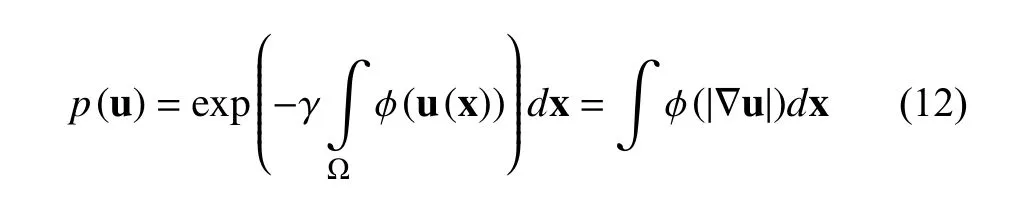
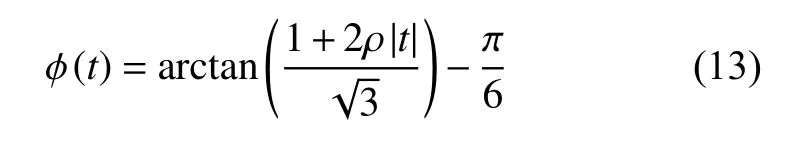
3 模型求解

我们利用变量分离技术和ADMM方法[10,22]对模型进行求解,同时为了处理非凸非光滑正则项,我们应用了多阶凸松弛方法对模型进行求解,虽然该方法仅导致原始非凸问题的局部最优解,但该局部解是对初始凸松弛的全局解的改进.此外,因为每个阶段都是凸优化问题,所以该方法在计算上是高效的.

求解(14)等价于求解如下的无约束问题:

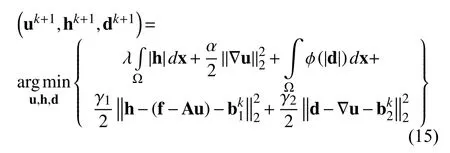
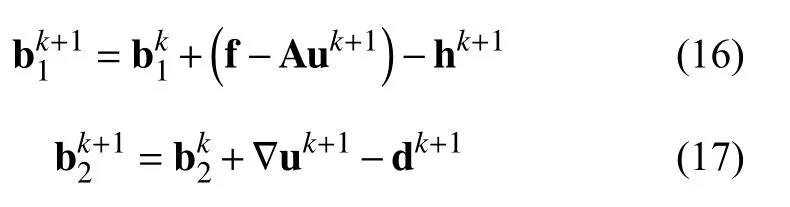
3.1 u-子问题

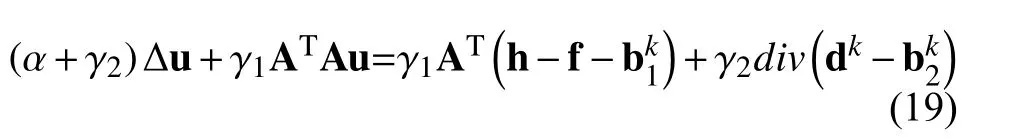
可以利用高斯赛德尔迭代或者FFT对上式进行求解.这里选择FFT对上式进行求解,求解结果如下:

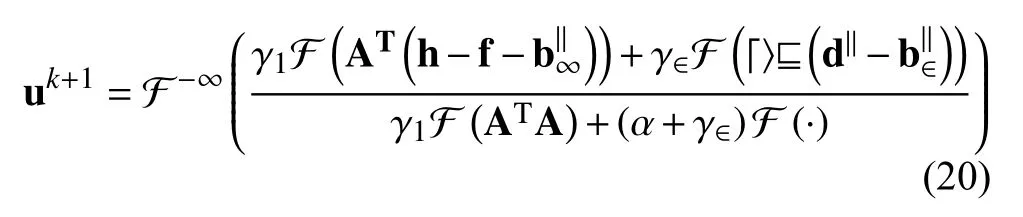
3.2 h-子问题

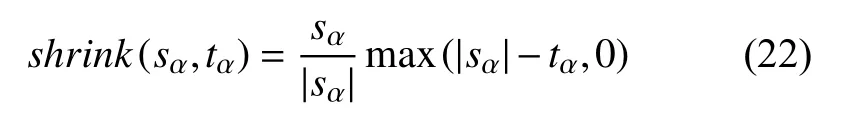
3.3 d-子问题

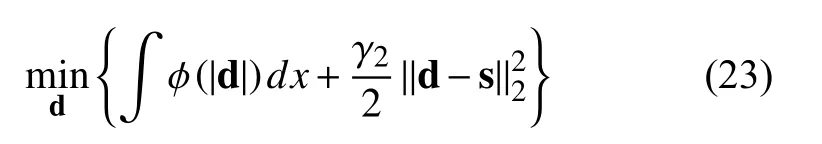
其中,

为了检验对脉冲噪声的去噪效果,设计了如下算法1.

算法1.脉冲噪声去除算法1) 初始化: 设 k=0,选择,;While “not converged” do 2) 计算: 用(20)FFT或者Gauss-Seidel计算;3) 计算: 用(21)计算;4) 计算: 用(24)计算;5) 间乘子更新:(),End while

4 实验分析

本节中,我们对该模型有效性进行了实验.首先我们使用遗传算法选择模型的最优参数,然后我们在多个不同噪声图像上与其他模型的去噪声效果进行比较.但是遗传算法可能陷入局部极值,所以我们对本文防止遗传算法陷入局部极值做了如下的处理.因为,产生局部收敛的原因之一是群体中多样性过早的减少,使得遗传算法的搜索空间大大减少,虽然到现在为止遗传算法对参数选择的控制还没有理论指导,但是我们可以用以下方法加以改进,在计算多样度时,保证群体中所有个体在某一基因位取相等值的个数不小于一定阈值,才允许多样度的计算有贡献.

本次实验中我们与TVL1,ROF以及论文SHI中的方法进行了比较,使用的图片有Lina,Cameraman,parrots,parrots.本次实验主要比较了图像去燥之后的ISNR,PSNR值如下:

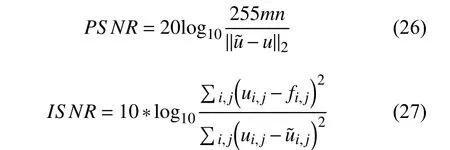
4.1 参数选择

该部分,我们主要讨论如何对参数进行选择,在我们提出的模型算法中,共有5个参数需要进行选择.通常参数选择的方法有两种: 第一种是通过实验人员的经验来设置[19–21]; 第二种方法是固定几个参数的值,修改其他参数的值来获得最优参数[7].

本次实验中,我们使用了遗传算法来寻找最优的参数.在我们的模型中,需要选择的参数是(a,b,c,d,…),其中(a>0,b<0,d>0).我们的目标是在参数空间中选择一个最优点.为此,我们假设最优点为使得在训练集P上的平均ISNR值最大的参数,遗传算法的目标函数为:

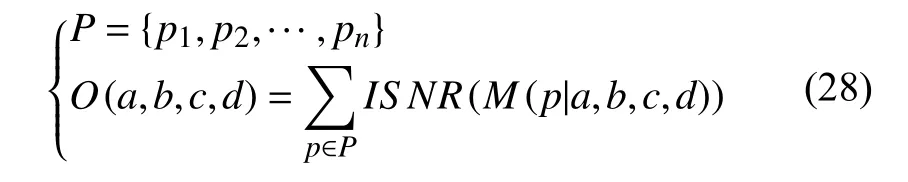
其中,pi为训练集中的图片,a,b,c,d为需要选择的模型参数,M代表提出模型,O为遗传算法的目标函数.

在遗传算法中,我们设置染色体个数为20条,遗传率为85%,繁殖代数为400.根据运行结果,我们选择的最优参数为:

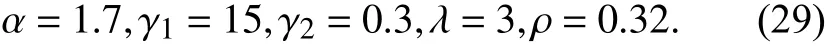
本文中,我们对不同模型在纯脉冲噪声图像上的的去燥效果效果进行比较.其中脉冲噪声主要考虑了椒盐噪声,噪声level分别为0.01,0.1,0.4,其中4种模型对不同级的椒盐噪声图像去燥的ISNR、PSNR结果如表1所示,去燥后的图片如图1所示.

表1 本模型与其他经典模型对脉冲噪声去燥效果指标对照

图1 模型对脉冲噪声去燥效果图

5 总结与展望

本文综合TVL1、ROF、模型STVL1(Squares TVL1)、Shi-模型,提出了非凸非光滑关于脉冲噪声去除模型,并使用变量分离技术的ADMM算法对模型进行求解,为了处理模型的非凸非光滑项,本文应用了多阶凸松弛方法对子问题进行了求解,利用遗传算法对模型参数进行选择,通过在不同图片及不同噪声上的大量实验表明,该模型的鲁棒性、运行时间和ISNR、PSNR都优于其他三种模型.并且该模型能够保持图像的局部信息具有更好的可视化质量.